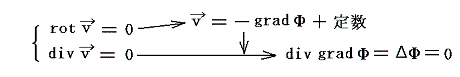こちらのバージョンをご利用になると鮮明に印刷されます。 目次付フレーム版 NOフレーム版
カルマン渦列(動的安定性解析)
流れが絡む多くの場面に出現し重大な影響を与える有名な渦列の説明です。この現象を理解するにはかなりの準備が必要ですが、なにとぞ御容赦ください。渦についてなじみのない方は、先に別稿「二次元・非圧縮性・完全流体の力学(ラグランジュの渦定理とは何か)」をお読み下さい。
1.渦列とは
(1)渦列が生じるメカニズム
1.渦シート
流れの中に物体を置くと、物体の背後に回り込む角の部分では、流速は無限大、圧力は負の無限大になる。
これは運動方程式から導かれたラグランジュの渦定理を適応した渦なし完全流体の流れに対する連続の方程式の要請によるものです。
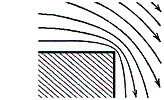
しかしそのような状況は物理的には不可能です。実際には角の部分で急に曲がるような流れは起こらないで、いわゆ止水領域が形成される。
流体が静止した陰の部分(止水部)が物体の背後にでき、流れはその表面を滑って流れようとする。そのとき止水部と物体の周りを流れて去って行く流れの境界面に流速の不連続面が生じ、無限大の速度勾配が生じる。しかし、流体には内部摩擦があるためその様な状況で互いに滑りあうことは不可能で、実際の流れでは、速度差調節用の渦シートが不連続面に沿って生じる(下左図)。
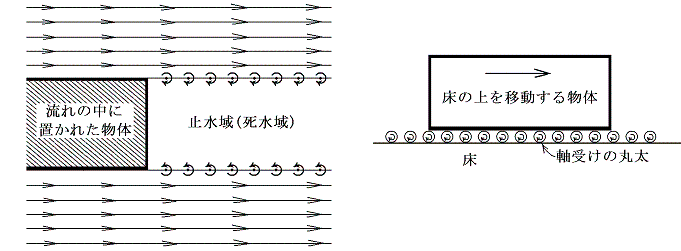
これは、ちょうど床の上に丸太を沢山並べてその上に物体を置いて動かすと、丸太がちょうどベアリングの軸受けの様な働きをして物体と床の速度の違いを仲立ちするのに似ている。このとき床の物体の間に挾さまっている丸太は物体の移動速度の半分で物体を追いかけるように転がっていく(上右図)。
[補足説明1]
しかしながら渦は丸太の軸受けのように簡単ではない。実際は渦は流体が流れ去る速度U0で流されながら、渦同士の相互作用のために渦に付加速度が生じて、それらが合わさった速度で流れ去っていく。その付加速度は流れの主流とは反対向きに生じる。そのため渦の移動速度は主流の流速U0の半分ではなくて、その0.80~0.86倍程度の速度で物体から離れてゆく。この当たりは後で詳しく説明する。
もし上記の状況を、静止した流体中を速度U0で物体が左方に動く場合だと考えると、渦は物体の移動速度U0の0.14~0.2倍の速度で物体を追いかけるように左方に動きながら、物体から離れていくことを意味する。またそのとき上記の止水域の流体は物体をU0で追いかけて行くことになる。つまり動く物体は、その背後に物体と共に動く流体質量を増大させながらそれらの流体部分を引きずって動いていくことになる。実はこれが流体が受ける抵抗力に関係するのだが、これも別稿「渦抵抗(カルマン渦列と抗力)」で詳しく説明する。
2.渦列への分裂
流れの中に置かれた物体の背後には止水域との境界面に沿って渦シートができるのだが、その連続的な渦シートは、やがて離散的な渦点に集約された渦の連なりとなる。つまり、流速の不連続面にできた渦の層は、一般に不安定で渦の層を巻き込んでいき、幾つかの渦点に集約される。渦シートが渦点に集約されるメカニズムは以下のよう説明できる。(プラントル著「流れ学」コロナ社 2章3.4節 or 谷一郎「流れ学」岩波全書p81
より)
仮に上流で小さい変化が起こり、そのために不連続面が波を打つものとしよう。波は不連続面の両側の速度の平均(q1+q2)/2で下流に伝わるから、この平均速度で動く座標から見れば、波の山も谷も静止し、不連続面の上下の流体は右または左にそれぞれ等しい速度で流れることになる。(下右図)
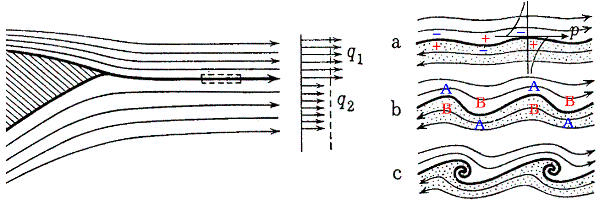
このような定常的な流れの中にごく僅かな乱れが生じて流れが波打つと、湾曲の外側では流線は密になり流速は増大する[上図A]。一方湾曲の内側では流線はまばらになり流速は減少する[上図B]。運動方程式から導かれるベルヌーイの定理によると、流速の大きなAの部分の圧力は減り、流速の遅いBの部分の圧力は増える。そのため流れに直角な方向の断面には境界面を挟んで上図のような圧力分布が生ずる。上図の(-)の部分で圧力が低く、(+)の部分で圧力が高くなっている。従って山はますます高く、谷はますます深くなり、波の振幅が増幅されて、波の山が巻き込まれて個々に分裂した渦の列となる。
流れの中に置かれた物体の背後には止水域との境界面に沿って渦シートができるのだが、その連続的な渦シートは、この離散的な渦点の連なりは、流れて去って行く流体を追いかけるようにして物体から離れて遠ざかっていく。
この当たりを最初に指摘して研究したのはヘルムホルツです。下記の論文または参考文献3.の§30等を御覧ください。
Helmholtz,"U¨ber diskontinuierliche Flu¨ssigkeitsbewegungen",Monatsber.
K. Akad. Wiss. Berlin 23. (1868), p215-228 [この論文は F. Guthrie によって英語訳されたものが Philos.
Mag.Vol.36,Series.4,(1868), p337-346,に "On Discontinuous Momentum
of Fluids"として掲載されています。これはGoogleBooksから無料でダウンロードできます。]
3.渦列の例
次の写真は鳴門海峡に生じた渦列です。大鳴門橋ができる前の古い写真ですが、上に述べた事柄の実例として興味深い。鳴門海峡を北から南に向かって流れ出る潮流と岬の陰の止水域とで速度差が生じる境界線上に渦列が生じている。
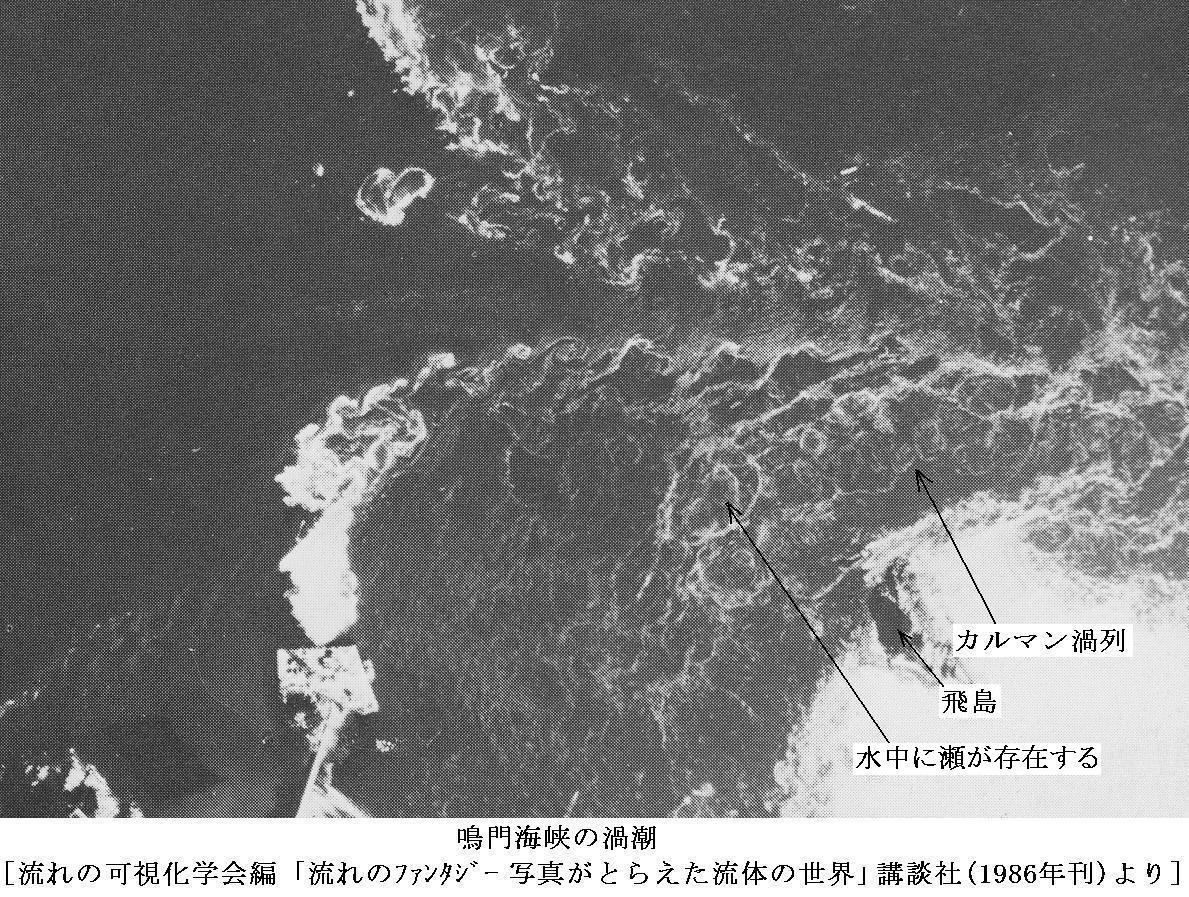
さらに興味深いのは写真下の飛島の北東(写真では飛島の左上)の水中に存在する瀬の背後にカルマン渦列ができていることです。季節風による雲のカルマン渦列の写真は多いのですが、潮流でできる例は珍しい。ちなみに明石海峡大橋の橋脚の背後にも綺麗なカルマン渦列ができるようです。
[2015年7月追記]
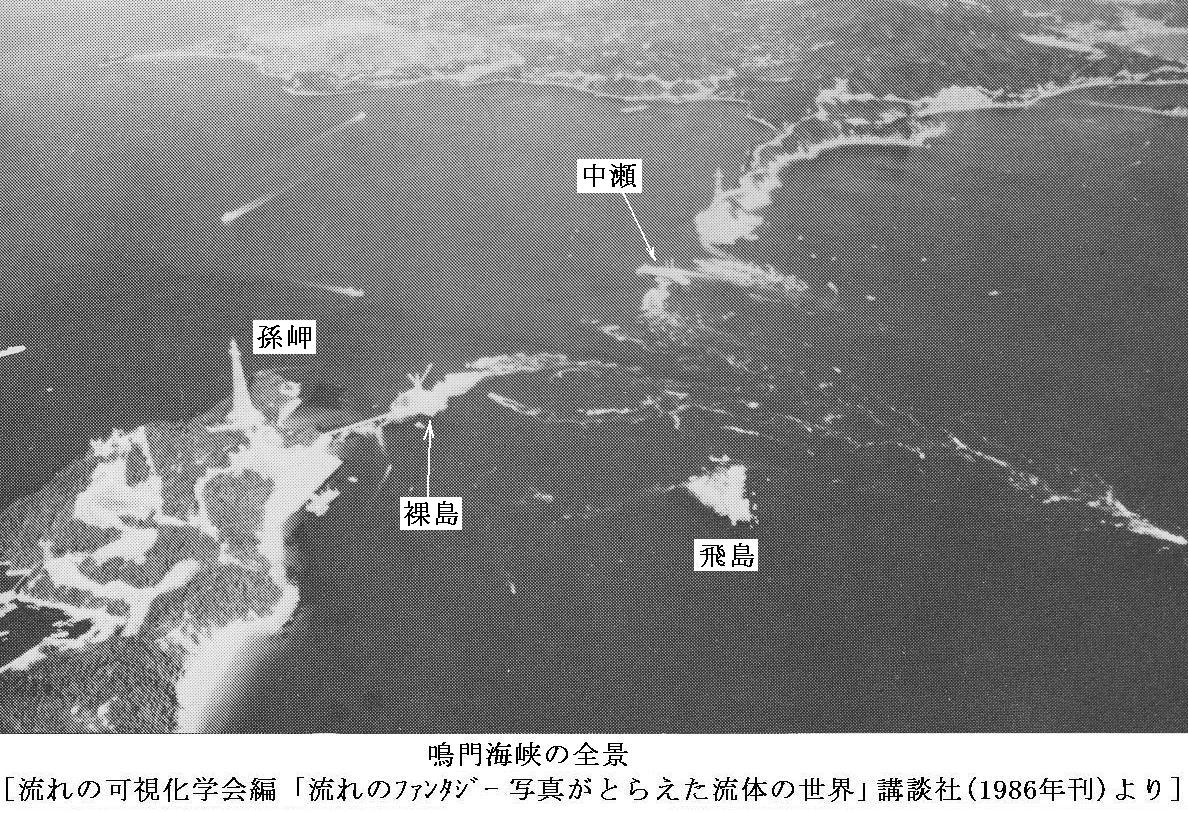
最近、地元の方からご指摘いただいたのですが、以前記述していた飛島の位置は間違っていました。図中に記した渦列の原因は水中の瀬のようです。その方から送っていただいた図を引用しておきますのでご覧下さい。
海底地形図1、海底地形図2、高空写真3
また、同じ方から上の写真の時期について、裸島に隣接して工事中の大鳴門橋の主塔橋台の建設状況から推察して昭和52~53年頃の写真だろうと教えていただきました。いずれにしてもご助言に感謝。
渦列の例について授業プリントから引用[拡大版]
《渦列の詳細》

《渦列の例》

(2)渦列の様子
このような渦列は誰でも簡単に観察できる。たとえば洗面器に張った水の表面に墨汁を一滴たらし、その表面に丸い細い棒(箸か爪楊枝)を立ててゆっくり動かすと、物体背後に2列の渦列ができることが墨の模様から見て取れる。[これは簡単にできる実験なので是非やってみられることを勧める。]
そのとき発生する渦は以下の写真に示すように、いつも特定の並び方と移動速度をもっている。

次の写真は物体から流れ出る色素の“流脈線”によって渦列を可視化したものです。(流脈線の意味は別稿の説明を参照)
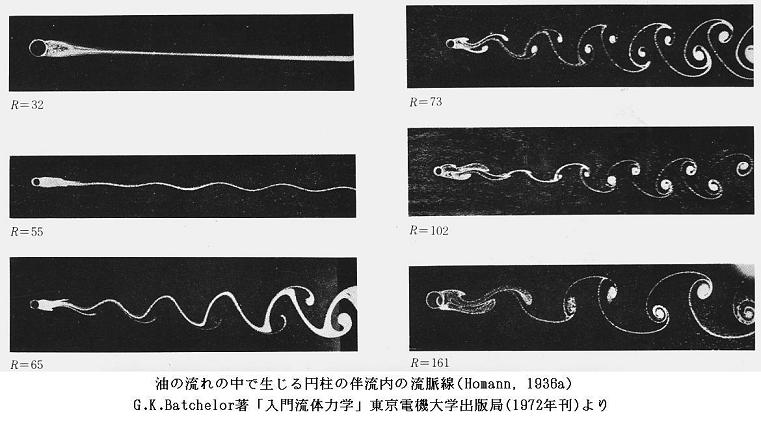
これは昔からよく知られている現象だったが、なぜ渦列の分布と移動速度が特定の配置と値になるか、その理由を考えてみようとした人は永い間いなかった。その謎を解明したのは、若き日のカルマン(1881~1963年)で1911年の事です。彼は後に、そのときの事情を回想して興味深い記述を残している。「カルマンの渦列について(カルマンの回想)」[参考文献4.、5.参照]。
この回想を読むとカルマンは、良く言われる渦列の安定配列の配置を明らかにしたこともさることながら、伴流抵抗のメカニズムを明らかにしたことが重要だと思っている様です。普通このことはあまり注目されませんが、確かにこの方がより画期的なことかも知れません。
2.数学的準備
カルマンが展開した理論の説明に入る前に数学的な準備をする。
(1)発散
1.定義
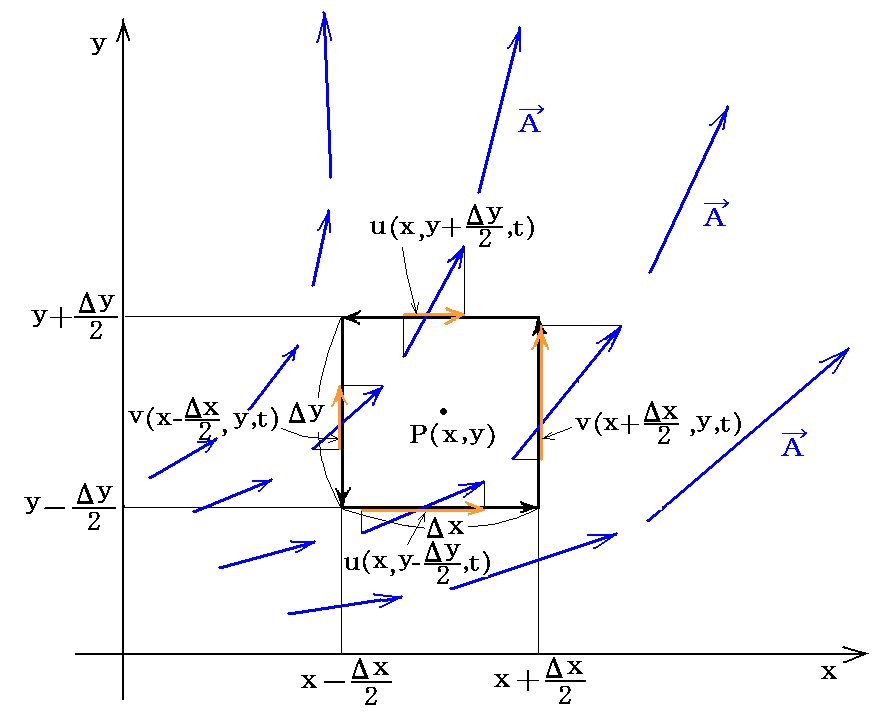
次図の様な速度場vが存在したとき、次式で定義されるmを点P(x,y)に於ける発散という。つまり、下図のようにxy平面上に存在する速度ベクトルvについて、微少な四角形ΔxΔyの各辺を横切る成分を積算する。
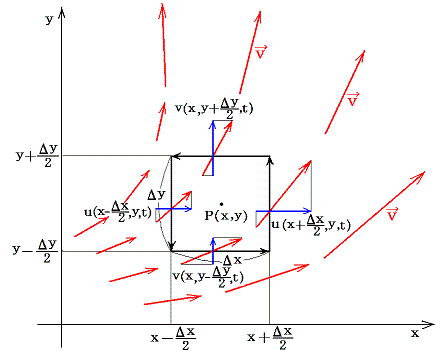
それぞれの辺を通過する流量を閉曲線に沿って加え合わせると

となる。ここで着目している面積素片の各片から外側に向かう場合が正になるように正負の符号は取られている。
これは小さな閉曲線を横切って単位時間に流れ出す流体の体積を意味する。今考えているような非圧縮生流体の場合は、境界線を越えて単位時間に流れ出す質量だと言っても良い。この値mが正ならばその点に単位時間当たり体積m(あるいは質量m/ρ)の湧き出しがあることになり、負ならば吸い出しがあることになる。
この議論を三次元に拡張すると面積素片は体積素片となり、各辺を横切る流量は微少六面体の各面積素片を横切る流量となる。上記のmも、元々は三次元上の各点(x,y,z)で定義できる量である。mは三次元の速度ベクトルvにベクトル演算divを施したもので、三次元の場合は上記の式に∂w/∂zが付け加わる。ただしwは速度ベクトルvのz軸方向の成分を表す。
2.補足
ここであげた例では、図示された領域の全ての部分で発散mがゼロでない値を持ちます。それは発散を計算するための微少四角形を様々な場所に動かして同様な計算をしてみれば直ちに了解できる。
発散mが全ての点でゼロになるためには連続の方程式(質量保存則)から明らかなように、流線が密になる所では速度ベクトルは大きくならねばならならず、逆に流線がまばらなところでは速度ベクトルは小さくならねばならないが、上図ではそのようになっていないので発散mが存在することがわかる。[この当たりは別稿の図を参照]
発散や湧き出しという言葉からは、あたかも流体領域の中に挿入されたパイプなどから流体が領域内に湧き出したり吸い込まれたりするような状況
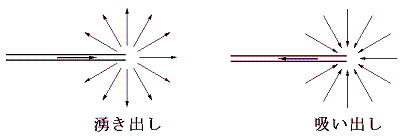
を想像するが、そのような状況が問題になることはまれで、実際は流体が膨張・収縮することに伴う現象だと考えた方がよい。
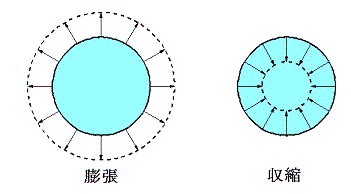
別稿の1.(2)1.の連続の方程式で説明したように

であり、流体の密度変化(膨張・収縮)がゼロでなければ、divvは有限な値となる。そのため発散は流体の圧縮・非圧縮性に深く関わっている。
(2)回転
1.定義
前節と同様な速度場vが存在したとき、次式で定義されるζを点P(x,y)における渦度という。これは速度ベクトルを小さな閉曲線リングに沿って積算すると、あたかも渦を巻くような成分があることを意味する。下図のようにxy平面上に存在する速度ベクトルvについて、微少な四角形ΔxΔyの周りに沿った成分を積算する。

それぞれの辺を通過する速度ベクトルの閉曲線に沿った方向の成分を閉曲線の長さ方向に加え合わせると
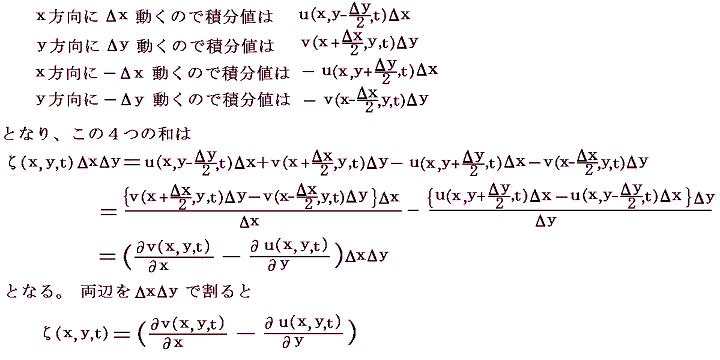
となる。閉曲線の経路に沿った方向の速度成分を線積分したものを循環という。渦度は、循環の閉曲線を無限に小さく一点に縮めた場合の値のことです。
渦度ζの正負は次のように決めてある。図の様に点P(x,y)に小さなサークルを考えて、z軸の負から正の方に向かってそのサークルを眺める。そして、そのサークルを右ネジの方向に回って速度ベクトルのサークルに沿った成分を積算したものが正なら渦度が正になるようになっている。
同様な議論はyz平面、zx平面についても成り立ち三次元の渦度ベクトルが定義できる。上記のζも、元々は三次元上で表される渦度ベクトルω=(ξ,η,ζ)のz成分である。つまり渦度ベクトルω(ξ,η,ζ)は三次元の速度ベクトルvにベクトル演算rotを施したものです。今は二次元の流れとしているのでx成分ξ=0、y成分η=0となり、z成分のζだけが残っていると考えればよい。
2.補足
上にあげた例では、図示された領域の全ての部分で渦度ζはゼロでない値を持ちます。それは渦度を計算するための微少四角形を様々な場所に動かして同様な計算をしてみれば直ちに了解できる。[この当たりは別稿の図を参照]
ここで注意してほしいことは速度ベクトル場が回転していることが渦度の存在を意味するのでは無いと言うことです。たとえば、回転速度がある点Qからの距離rに逆比例するような回転のベクトル場の場合
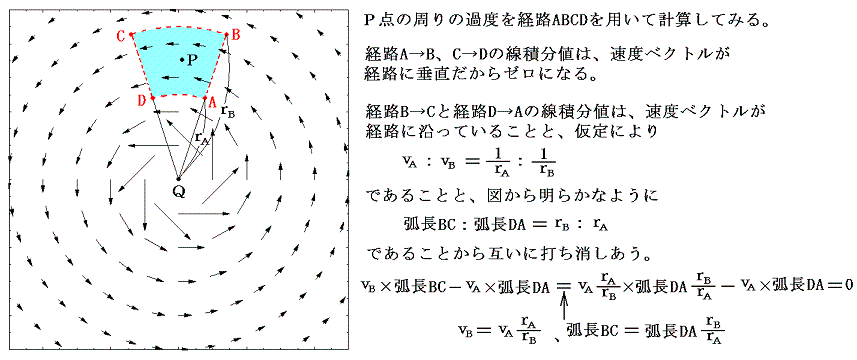
となる。この例の様に流体が回転するように流れていても中心のQ点以外では、渦度は全てゼロの渦無しの流れなのです。点Qにおいてのみゼロでない渦度を持つ。実際、中心点以外でrotv=0であることは速度ベクトル場
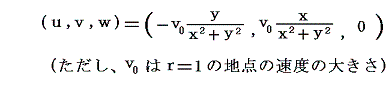
にrot演算を施してみれば、直ちに了解できる。この例はきわめて教訓的です。
(3)ベクトル解析の基本定理[ヘルムホルツの定理]
前節2.(1)、(2)で説明したように、ベクトル場vの大きさの変化の様子が発散mを決め、ベクトル場vの曲がり具合(回転)の変化の様子が渦度ζを決める。そのとき、逆にあらゆる場所の発散mと渦度ζの値が与えられたらなばベクトル場vは完全に決定できるのであろうか?実はその通りなのであって、このことは数学的に証明される。それが次に述べるベクトル解析における基本定理です。
これはストークスの流体力学に関する大論文[G.G.Stokes, On the dynamical theory of diffraction,
Transactions of the Cambridge Philosophical Society vol.9, p1-62 (1849),または
Mathematical and Physical Papers, Vol. II, p243-328.特にp254-257 (Cambridge
University Press, 1883)これはGoogleBooksからダウンロードできます]で最初に証明された。
また後に、ヘルムホルツは渦の運動に関する論文[H.Helmholtz, U¨ber Integrale der hydrodynamischen
Gleichungen, welche den Wirbelbewegungen entsprechen, Journal fu¨r die
reine und angewandte Mathtmatik, vol.55, p25-55, 1858(これはGoogleBooksからダウンロードできます)]でより完全な形で与え、渦理論の基礎とした。そのため、この基本定理をヘルムホルツの定理と言うこともある。
これらの定理を含めて、流体力学で開発された様々な数学的テクニックは電磁気学の研究と相補いながら発展するのですが、電磁気学の構築(ちなみにマクスウェル”Treatise”の出版は1873年)においても絶大な威力を発揮する。
この定理の証明は三次元で行う方が解りやすいので、以下では三次元で説明する。
連続な無限空間で定義され、無限遠においてその値が1/r2程度でゼロになる任意のベクトル場 v は、渦無しの場 v1 と発散の無い場 v2 の和で表すことができる。
これは

を意味しており、この分解でベクトル場vの発散m(湧き出しor吸い込み)をv1に受け持たせ、渦度ωをv2に受け持たせる
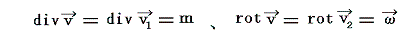
ことであり、その分解の仕方が定数ベクトルを除けば一意に定まると言うことを意味する。以下三段階に分けてこのことを証明する。
1.ベクトル場v1の導出
rotv1=0である 渦無しのベクトル場 v1 はスカラーポテンシャルΦを用いて
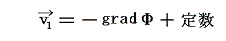
と表すことができる。そのようにできることは、二次元の場合については別稿の4.(2)1.で、三次元の場合はこちらで証明する。
このときv1の表現式に付け加えた定数だけ不確かさが残るのが、v1を導くに際しては何の役割もしないので省略しても良い。
またgradの前の負符号-は、Φをポテンシャルの山と考えて速度ベクトルが山を転がり落ちる方向を向くとした方がイメージしやすいから付けたのであって、それ以上の意味はない。以後の議論では+でも全く差し支えない。
さらに、rotgradΦ=0 は恒等的に成り立つ[成分表示で計算すると直ちに証明できる]ので、当然のことながらrotv1=0を満足している。
このとき、Φは次の微分方程式を満たさねばならない。

右辺がすべての点で与えられている場合、この非斉次ポテンシャル方程式[Poissonの方程式]の解Φはグリーンの定理をもちいて求めることができる。
数理物理学における大定理であるグリーン(Green)の定理は別稿で証明するが、ここではその結論を用いる。
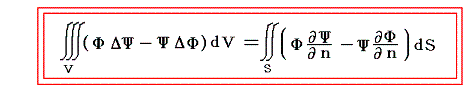
の形のグリーンの定理においてΦ=スカラーポテンシャル、Ψ=1/r とすると、以下の重要な結論が得られる。ただしrは空間内の任意の積分動点Q(x',y',z')から一つの定点P(x,y,z)に至る距離で
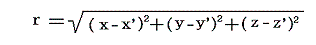
のことです。上記の積分においてP点が体積積分の領域Vの中にある場合と外にある場合で取り扱いが異なるので分けて考える。
[点Pが積分領域Vの外部にある場合]
この場合には積分動点Q(x',y',z')が積分領域V内をどのように動いてもrはゼロになることは無いから1/rは有限です。
このときよく知られているように 1/r はLaplaceの方程式ΔΨ=0を満足する。このことはrを(x,y,z)と(x',y',z')の成分で表し体積積分を実施する場所の座標(x',y',z')についてラプラス演算の微分を地道に計算してみれば直ちに証明できる。これは高校で習う分数関数の微分の計算です。このとき(x,y,z)の微分ではなく(x',y',z')の微分であることに注意。従ってΔΨ=Δ(1/r)=0となるので上式は
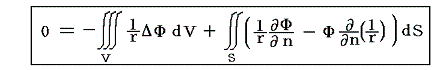
となる。
[点Pが積分領域Vの内部にある場合]
この場合には積分動点Qが定点Pに近づくとr=0となり、1/rもΔ(1/r)も不定になる。従ってΦ、Ψのいずれも有限確定な連続関数であるという仮定の下に得られたGreenの定理をそのまま使うことはできない。そのためP点を中心とするきわめて小さい半径εの球面σを描いて、その内部を積分領域Vから取り除いて、残りの領域V’に対してGreenの定理を適用することにする。
ただし、このようにすると面積分は、はじめからVの境界であった閉曲面Sに付け加えて、新しくV’の境界として現れた球面σに対しても実施しなければならない。閉曲面σに立てた外向き法線は点Pの方向を向いていることを考慮すると、次のように変形される。ここでdσは球面σの上の面積素片であるが、これが中心Pに対して張る立体角をdΩとすると、dσ=ε2dΩとなる。また領域V’内ではΔΨ=Δ(1/r)=0がいえるので

となる。すなわち、領域Vの中のすべての点においてΔΦが与えられ、領域Vを囲む閉曲面Sの上でΦおよび(∂Φ/∂n)が与えられている場合、P点におけるΦの値ΦPは上記の式で与えられる。
補足すると、先ほど求めた[点Pが積分領域Vの外部にある場合]の式
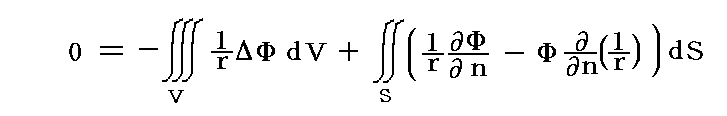
は、積分領域Vとそれを囲む閉曲面Sを十分大きく取ったとき、その領域外のΦpが常に0となる事を示している。
ここで。さらにΦもLaplaceの方程式を満たし領域V’内の至る所でΔΦ=0となる場合には
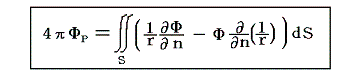
となる。これを[Greenの公式]と言う。これは大変重要な式で3.(1)2.で用いる。
領域Vが無限に広がっており、無限遠においてΦが1/rと同じ程度にゼロになれば、前述の式の右辺第二項の表面積分の項はゼロになるので

が得られる。ただしV∞は無限に広い領域を表す。ここでさらに、ΦがPoissonの方程式
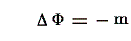
を満足するならばm(湧き出し)がゼロでない領域に付いて積分して
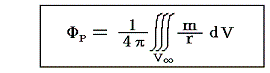
となる。これは、まさしく領域のすべてにおいてmが与えられている場合、任意の点P(x,y,z)におけるΦ(x,y,z)の値を与える式である。mは積分動点Q(x',y',z')における値で、rはP(x,y,z)とQ(x',y',z')の間の距離
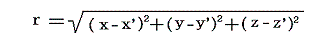
であり、dV=dx'dy'dz'である。積分はm(湧き出し)がゼロでない領域内で点Qを動かして実施する。mは点Q(x',y',z')における値を意味し、grad演算は点P(x,y,z)の座標に関するものであり、ベクトルrは積分動点Qから定点Pに向かうものであることに注意して、上記の式を用いれば、求めるべきベクトル函数v1は
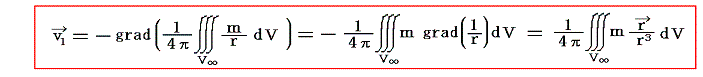
で表される。湧き出しmの分布が有限の領域に限られる場合には、こようなベクトル関数v1は、無限遠において1/r2の程度で0に近づくので、最初の条件を確かに満たしている。
[補足説明1]解の例
[点Qの位置のみに強さmdVの発散(湧き出し)がある場合]
この場合体積素片dVの境界面から単位時間に外部に流れ出る流体体積がmdVと言うことです。上記の解は点Qから距離rだけ離れた位置の速度ベクトルはQから外向きに放射状に向き、その大きさが距離の二乗に反比例して小さくなることを教えてくれる。つまり下図のような状況になる。
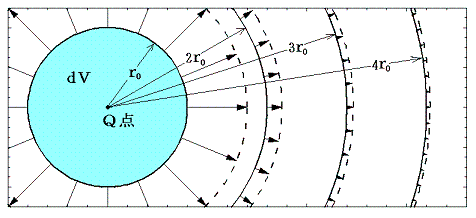
Q点以外のあらゆる位置の発散(湧き出し)が全てゼロであるから、2.(1)2.で注意したように、これはQ点以外の領域の流体は非圧縮性であることを意味する。上記の解は非圧縮性流体が満たすべき連続の方程式を満たしている。なぜならQから半径rだけ離れた位置の球面の面積は4πr2で与えられるが、その面を横切る流体速度は1/(4πr2)に比例して小さくなるのだからQ点以外のあらゆる半径の位置で質量保存速を満たすように動いていることになるからです。
前記の結論は、このような単独の湧き出し点の解を重ね合わせればよいと言っている。これはある意味、当然の結果です。
2.ベクトル場v2の導出
divv2=0である 発散の無いベクトル場 v2 はベクトルポテンシャル Aを用いて

と表すことができる。そのようにできることはこちらで証明する。このときv2の表現式に付け加えたgradφはrotgradφ=0が恒等的に成り立つので、ベクトルポテンシャルAにはgradφだけの不確定さが残ります。ところが、実際にv2を求めるときには必ずrot演算を行うのでこの項は何らの役割もしない。そのため、これを省略しても良い。
このとき、div(rotA)=0 は恒等的に成り立つ[成分表示で計算すると直ちに証明できる]ので、当然のことながらdivv2=0を満足している。
このとき、Aは次の微分方程式を満たさねばならない。下記のベクトル公式の証明はこちらを参照。
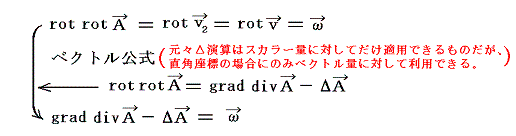
ここで、ベクトル場Aとして、

を満足するようなものを選ぶことにする。なぜそのようなものを選ぶのかというと、graddivAの項が省略できるからです。そのため、Aを求める偏微分方程式は
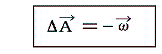
の様なきわめて簡単な形にできる。ベクトル関数A=(Ax,Ay,Az)を直角座標の成分に分解すると、これは三つのPoissonの方程式となる。
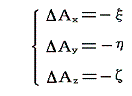
これらは、それぞれがスカラー関数のPoissonの方程式だから、前項と全く同様の方法で解を求めることができる。つまり
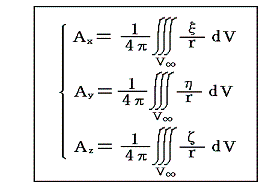
となる。これはすべての領域においてω=(ξ,η,ζ)が与えられているとき、任意の点P(x,y,z)におけるベクトル関数A=(Ax,Ay,Az)の値を与える式です。ω=(ξ,η,ζ)は積分動点Q(x',y',z')における値ξ(x',y',z')、η(x',y',z')、ζ(x',y',z')で、rは定点P(x,y,z)と積分動点Q(x',y',z')の間の距離
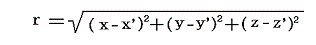
であり、dVは点Qにおける体積素片dV=dx'dy'dz'です。積分はω(渦度)がゼロでない領域内で点Qを動かして実施する。
[補足説明1]
ここで、上記の解がdivA=0を確かに満たしていることを証明しておかねばならない。
Axをxで偏微分(x’ではないことに注意)すると
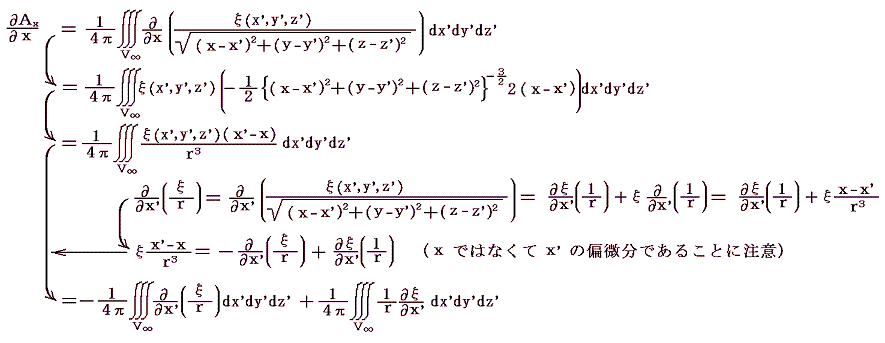
となる。Ay、Azについても同様な式が得られて
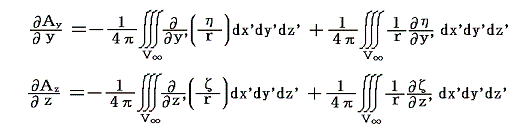
となる。これらを加えると
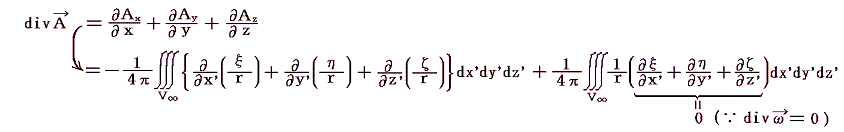
となる。ここで流体内の至る所でdivω=divrotv=0[ベクトル演算divrotが恒等的にゼロであることは成分表示で計算すれば証明できる]であるから、右辺第二項の積分はゼロとなる。第一項の体積積分をGreenの定理[Gaussの定理]を用いて表面積分に直すと
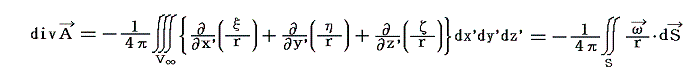
となる。渦度が分布する領域が有限であれば、これを取り囲む閉曲面を充分大きくとると曲面上でω=0[当然、面積素片に垂直な成分ωnもゼロ]となるので右辺はゼロになり、divA=0が証明できる。
上で求めたベクトル関数A=(Ax,Ay,Az)の解を用いれば求めるべきベクトル関数v2は
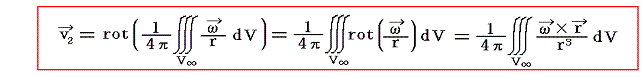
となる。ここで、ωは点P(x,y,z)ではなくて積分点Q(x',y',z')での値であり、rot演算は点Q(x',y',z')ではなくてv2を求める点P(x,y,z)に関してのものであることに注意。成分表示は以下のようになる。
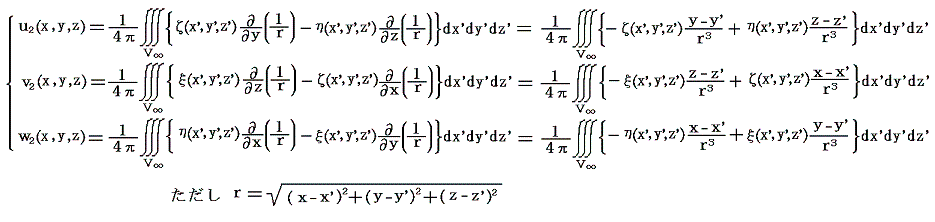
渦度ωの分布が有限な領域に限られる場合、このようなベクトル関数v2は、無限遠において1/r2の程度で0に近づくので、最初の条件を確かに満たしている。
[補足説明2]解の例
[渦糸の微少要素]
解の意味を考えてみる。最初にdVを別稿で考察した渦糸の微少要素と考える。つまり
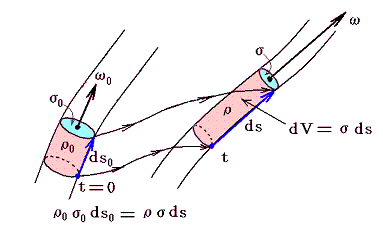
とする。このとき、積分動点Qにおける体積要素dV=σdsが点Pにおける流体実質部分に生じせしめる速度成分δvは上記の結論から明らかなように
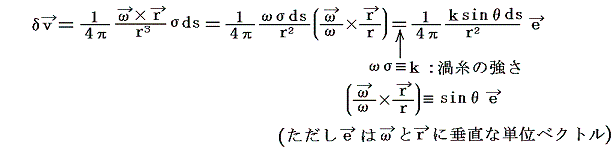
となる。ここでθはベクトルωとベクトルrのなす角度です。
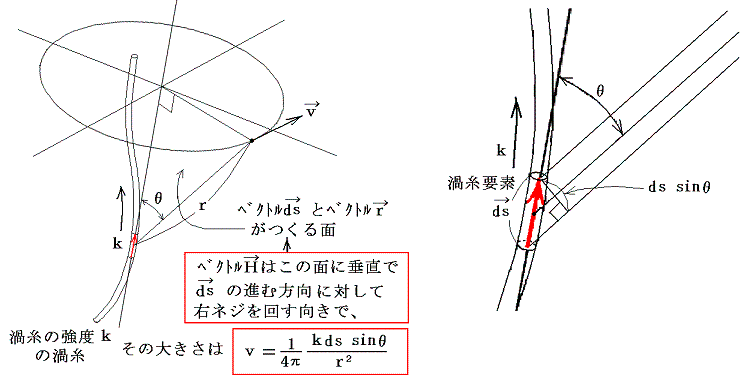
ここで渦糸の強さΓを電流Iに置き換えれば電磁気学におけるビオ=サバール(Biot=Savart)の法則と同じです。つまり渦糸による流体の速度は、その渦糸と同じ形の導線に電流Iを流したときの周囲の磁場を求めるのと全く同じ計算をすればよいのである。そのとき電磁気学では磁力線が導線をとり囲んでいるように、流体力学では流線が渦管をとり囲んでいる。
[直線状渦糸]
別稿で説明したように、ある決まった時刻について1本の渦糸(渦管)を考えると、その側面を一周する閉曲線Cについての循環は、Cを選ぶ場所によらず、渦管に固有の不変量です。そのため渦糸(渦管)が一旦ある点から始まれば、循環が一定[渦糸の強さが一定]であるから、渦糸の断面積が∞にでもならない限り過糸の強さはある有限な値で何処までも伸びていることになる。つまり、渦糸(渦管)は流れの中で中断することはなくて、流体領域の境界面まで伸びているか、あるいは自分自身で閉じた渦輪を作るかのいずれかです。

上左図の例が別稿で説明した空気砲が作る渦輪であり、開口部から流体が吹き出す流れでしばしば観測されるものです。現実問題では上右図の状況が重要です。浅い水路を流れる流体中の渦は水底と大気層を二つの平行境界面とする場合です。また竜巻や海峡の潮流に生じる渦も近似的にはこのようなものだと考えて良い。あるいは、気象学における台風や低気圧・高気圧の渦もその直径(数百~数千km)が大気の厚さ(10~15km)に比較して何倍も大きいので、やはり二つの境界面に接する渦の性質を持つ。
さらに、太陽黒点中には太陽流体の強い渦があることが知られているが、これは太陽内部を走る渦糸が表面に出てきているのである。そのため各黒点には渦の回転方向が逆の黒点が付随しており、反対半球上の対称的な位置に必ず存在する。そして半円状の渦糸が太陽流体内部を通って両者を結びつけていると考えられている。このような渦が生じるのも太陽が自転しているためであろう。
ここで断面積σの無限に長い直線上の渦糸が一本だけ存在する場合を考える。この場合には、渦糸に垂直な全ての平面内の運動が互いに等しい。すなわちz軸を渦糸に平行にして、渦糸に垂直なxy平面をとれば流体の運動はxy平面内の二次元的なものとなる。渦糸がxy平面を切る点を(x’,y’)とすれば、(x’,y’,z’)なる点を中心とする渦糸の線素ds=dz’によるxy平面上の任意点(x,y)における速度成分(δu,δv,δw)は、ξ=η=0、ζ≠0なることを考慮すると前出の式から

となる。ここでζσは渦糸の強さで、これをkで表すことにすると渦糸全体による速度の成分は次のように求まる。
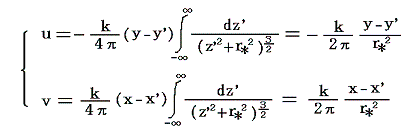
ここで
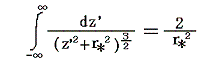
となる積分を用いたが、これはすでに別稿の2.(3)で証明している。
つまり、ある点に断面積σの渦糸があると、その渦(二次元の渦糸の強さをk=ζσとおく)によって誘起される流れの速度ベクトル場は、大きさqが渦からの距離rに反比例した
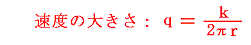
となり、方向が動径方向に垂直となる。
三次元の公式との違いはq∝1/(4πr2)ではなくてq∝1/(2πr)となっていることであるが、両者の違いはzに関する積分によって説明される。
この例において渦糸の周りの流体は渦糸の周りを回転するように流れるが、2.(2)2.で注意したように、それら流れの部分の渦度はいずれもゼロで、渦度が存在するのは渦糸の断面σの領域のみです。つまり、渦糸を取り囲んだ閉曲線リングに沿って、リング方向の速度成分を加算するとゼロにならないが、渦糸をそのなかに囲んでいない閉曲線リングに沿う同様な積分は常にゼロになる。流体力学的に言えば、渦糸の存在する断面積σ内のみに渦度ωが存在し、それ以外の部分は渦無しの流れと言われるものです。
前記の結論は、このような単独の渦糸の効果を重ね合わせれば良いと言っている。そのとき2.(2)2.で注意したように渦糸のまわりの流体は回転するように流れていても渦度ωはゼロなのです。ここが、この解の解釈で最もわかりにくい所ですが、ある一点に渦度が存在すると言うことは、その周りの流れに関してそのようなものであることを意味している。
[補足説明3](前野昌弘著「相対論講義録2010年度(平成23年2月4日版)」p97~98より引用)
ここで、スカラーポテンシャルφやベクトルポテンシャルAとは何なのかを補足します。これらの量の説明は前野氏の解説が秀逸なので前野氏のHPからそのまま引用しています。前野氏は電磁場の場合で説明されていますので、スカラーポテンシャルφをつくるものは、湧き出しや吸い込みではなくて電荷となります。またベクトルポテンシャルAを作るものは渦糸では無くて電流になります。
下記左図の○に+の記号の位置に電荷が存在する。また右下図の黒矢印の位置に電流密度素片が存在するとします。本来電流は渦糸と同じく連続した回路となるのですが、その一部が取り出されていると考えて下さい。
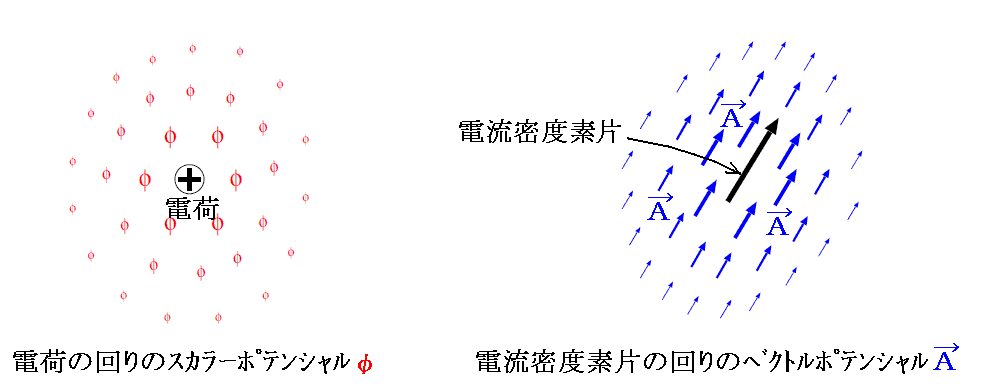
上左図の電荷の回りのφの値を決めるのが、すでに求めた解
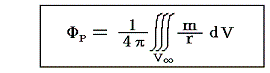
です。図はφ記号の大きさで、その値の大きさと分布の様子が示されています。φの大きさは電荷からの距離に反比例して小さくなる。もちろん上式の湧き出しmは電荷密度ρに置き変わります。そして、電荷がたくさん分布している場合は、それぞれの電荷が作るスカラーポテンシャル場を重ね合わせたものになります。
また上右図のAベクトルの分布を決めるのが、すでに求めた解

です。図の青矢印の分布でベクトルポテンシャルAの分布の様子が示されています。ベクトルAの方向がすべて電流密度素片の方向を向き、その大きさは電流密度素片からの距離に反比例して小さくなります。もちろん上式の渦糸密度ベクトル(ξ、η、ζ)は電流密度ベクトル(jx、jy、jz)に置き換わります。もちろん電流密度素片が連続的に分布して回路を作る場合は、それぞれの電流密度素片が作るベクトルポテンシャル場を重ね合わせたものになります。
スカラーポテンシャルの意味は別稿「保存力」で説明した二次元の場合のポテンシャルの山を三次元に拡大したもので尽くされています。もし電荷qがスカラーポテンシャル場φの中に存在するとqφという位置エネルギーを持つことになり、場φの大きさの勾配に従った力を受けることになる。
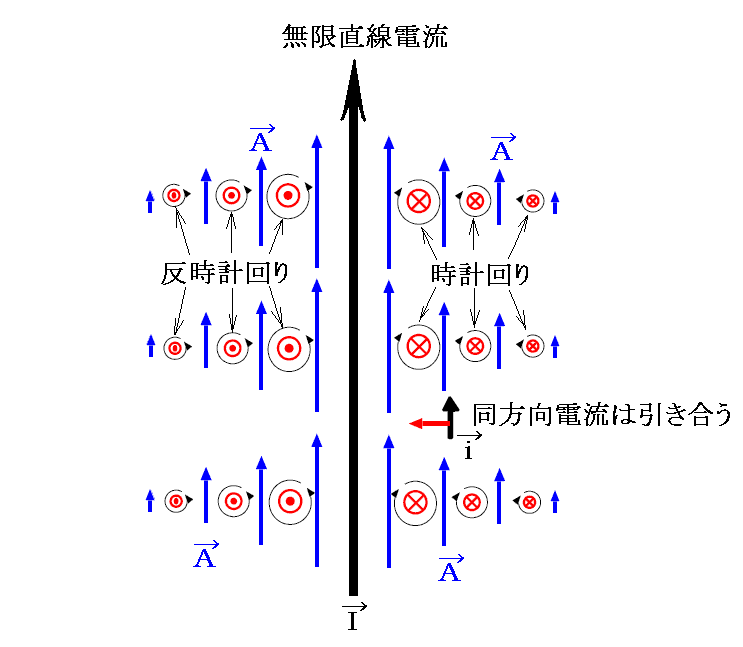
ベクトルポテンシャルの意味を、上図の電流密度素片が縦方向に無限に連なった無限直線電流の場合で説明します。無限直線電流が作るベクトルポテンシャルAの分布は、上記の電流密度素片が作るベクトルポテンシャルを重ね合わせたものになりますから、下図の様に直線電流の回りに、直線電流の方向を向いて分布し、その大きさは距離に逆比例して小さくなります。
このベクトル場Aを流れの流速を表す様なものだと見なして、2.(2)で説明した回転演算rot
の意味を適用する。
一つ前の図の青矢印で示した流れの場Aは導線の左側では反時計回りの渦を、導線の右側では時計回りの渦を生み出す。実際ベクトル演算rotAはその渦の回転を右ネジと見なしたときネジの進む方向のベクトルを意味する。このrotAこそ電磁気学における磁場ベクトルBであり、流体力学における流速ベクトルです。
つまり磁場B=rotAは導線の回りに渦を巻くように存在することになる。一つ前の図の赤丸に赤点は手前向きの磁場ベクトルBを赤丸に赤×は向こう向きの磁場ベクトルBを表す。その○の大きさが磁場ベクトルBの大きさを表している。
このようなベクトルポテンシャル場の中に電流素片 i を入れるとローレンツの力の法則に従った力を受けるので、電流素片 i は一つ前の図中赤矢印方向の力を受けることになる。
つまり、ベクトルポテンシャルAと同方向の電流要素 i はベクトルポテンシャルAが増大する方向に力を受け、ベクトルポテンシャルAと反対向きの電流要素 i はベクトルポテンシャルAが減少する方向の力を受ける。これはちょうど-電荷がスカラーポテンシャルφが増大する方向に力を受け、+電荷がスカラーポテンシャルφが減少する方向に力を受ける事情によく似ている。
まさに、それら分布状況がポテンシャル(位置エネルギー)を表している。
3.分解v=v1+v2の一価性の証明
仮にvの分解がv1とv2のほかに、異なった分解v1’とv2’が存在したとする。
このとき渦無しベクトルv1’-v1は同時に湧き出しも無くなる。なぜなら

だからである。
同様に、湧き出し無しのベクトルv2’-v2は同時に渦無しである。なぜなら

だからである。
そのときベクトルv1’-v1とv2’-v2に対するスカラーポテンシャルΦとベクトルポテンシャルAを求める計算は、1.と2.で求めた式で行われる。そのとき両ベクトルともあらゆる領域でm=0とω=0を満足するから、あらゆる領域でΦ=0であり、A=0となる。だからv1’-v1=定数、v2’-v2=定数となり、vをv1とv2に分解するやり方は、定数を除いて一義的である。
無限領域に付いてのベクトル場vの場合には、v1=-gradΦ+定数 と v2=rotA+gradφ の中の不確定要素 定数+gradφ は互いに打ち消しあわねばならない。なぜなら、この議論の最初の仮定によれば無限遠においてv=v1+v2はゼロでなければならないからである。
4.有限領域の場合
以上の議論はすべて領域が無限遠まで広がっている場合であるが、領域が有限な場合にはもう少し考察が必要です。領域が有限の場合2.(3)1.で求めた
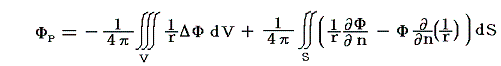
において右辺第二項の面積分がゼロにならない。そのため領域内の至る所でdivv=mおよびrotv=ωが与えられているばかりでなく、境界面上でΦの値と、外向き法線方向のv=-gradΦの成分vnが与えられている必要がある。
このとき、有限領域をV、その境界面をSとし、Sの外部にあって無限遠まで広がっている領域をV’とする。最初は境界面Sの上の条件を考えないで、Vの内部の至る所で、その発散(divv’=m)および回転(rotv’=ω)が与えられた値を取り、V’においては、その発散および回転が全く任意に与えられた値をとって、しかも無限遠においては1/r2の程度で0になるようなベクトル関数をv’とする。これはすでに述べた方法でただ一通りに決定することができる。
ところが、このような関数v’は求める関数vに対する境界条件(境界面Sにおける)を一般に満足しない。すなわちv’の境界面S上での外向き法線成分vn’はvnとは異なった値となる。
そこで、境界条件を満足する解にするために、Vの内部では至る所でdivv”=0、rotv”=0であり、かつ境界面Sの上におけるその法線成分vn”がvn”=vn-vn’となるようなベクトル関数v”を求める。このようなベクトル関数が求まるとき、v=v’+v”とすれば、これこそ我々が求めたいベクトル関数となる。なぜなら、このvは領域内のmやωの分布を満足し、境界Sにおける法線成分vnも満足しているのだから。
このときv”を求める問題は、ポテンシャル論における第二種境界値問題(ノイマン問題)と言われるものに帰着する。v”はrotv”=0を満足するので、すでに述べたようにv”=-gradψのようなスカラー関数ψが存在する。これをv”に対するもう一つの条件式divv”=0に代入するとdivgradψ=0となるので、ψはΔψ=0[Laplaceの方程式]を満足しなければならない。一方境界面Sの上ではvn”の値が知れているのであるから、Sの上のすべての点において(∂ψ/∂n)の値は与えられた値をとらねばならない。結局以下の定理に帰着する。
[ポテンシャル論における第二種境界値問題(ノイマン問題)]
領域Vの内部の至る所でLaplaceの方程式Δψ=0を満足し、かつその境界面Sの上で(∂ψ/∂n)が与えられた値をとるようなスカラー関数ψは、任意付加定数を除き、ただ一通りに決まる。
[証明]
仮に同じ条件を満足する他のスカラー関数ψ’が存在するとする。ここでψ-ψ’=Φと置く。そうすると、Φは領域Vの内部において至るところΔΦ=0を満たし、また境界面S上では(∂Φ/∂n)=0を満たす。
ここで別稿で証明したGreenの定理を用いる。今回は
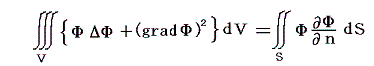
の形のものを用いる。この式のΦを上記のΦだとすると、ΔΦ=0 and (∂Φ/∂n)=0 だから
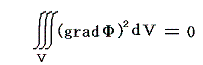
となるが、被積分項(gradΦ)2は必ず正か0であるから、積分が0になるためには至る所で
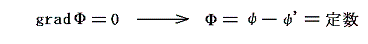
で無ければならない。つまり二つの解ψとψ’は任意の付加定数しか違わない。
[証明終わり]
このようにしてψは任意の付加定数を除き、ただ一通りにきまることが証明される。そのためベクトル関数v”=-gradψは完全に一通りにきまる。定数の勾配はもちろん0となるからである。
3.渦列の一般論
前章の数学的議論には流体力学の連続の方程式も運動方程式も出てきていない。これらの方程式と前章の議論はどのように関わっていくのかをここで説明する。
(1)数学理論と流体力学
1.非圧縮性・完全流体の流れ
非圧縮性流体において成り立つ連続の方程式から
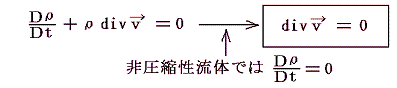
が常に成り立つ。そのため非圧縮性流体の流れは至る所で発散が無い流れであるといえる。そのため前章の結論の渦度ωのみが存在するベクトルv2が流れの解vとなると言える。
つまり、前章2.(3)2.の結論を用いれば、流れの任意の位置における速度ベクトル場vは渦度ベクトル場ωの分布と

の関係で与えられる。
このとき、別稿3.(3)で説明した完全流体の運動方程式から得られるラグランジュの渦定理により、渦無し(ω=0)の流体実質部分はその後も渦無しであり続け、渦糸を形成する渦あり(ω≠0)の流体実質部分はその後もその渦度を保ち続ける。
2.動く物体のまわりの流れ
最初静止している無限に広がる流体の中を物体が動くとき、その周りに生じる流れを求める。今は非圧縮性・完全流体を仮定しているから至る所発散がゼロの流れである。また、最初静止しているので渦無しを満たしている。そのため、その後生じる流れもラグランジュの渦定理[別稿3.(3)3.参照]により渦なしの流れである。つまり、その後も常に
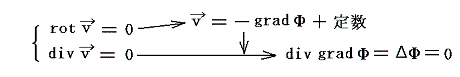
が満足される。つまり速度場は各点において定義できる速度ポテンシャルΦからv’=-gradΦで求まり、さらにその速度ポテンシャルΦは流体中の至る所でΔΦ=0を満足する。この式が成り立てば2.(3)1.で説明したGreenの公式が成り立つので、これを用いれば無限遠まで広がっている流体中を動く物体の周りの流れを求めることができる。
つまり、物体の境界面を内部境界Sとし、外部境界Σとしてきわめて大きな半径Rの球面Σを考える。球面Σの中心をPとする。Pは流体内部にあって今まさに速度ベクトルvを求めようとしている点である。そうすると[Greenの公式]は
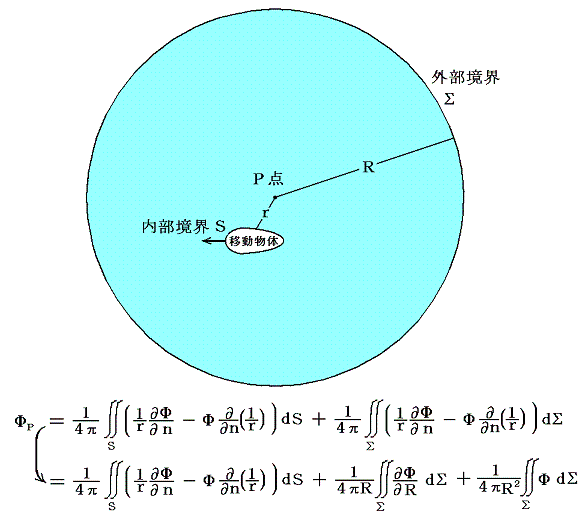
となる。ここで右辺の第二項、第三項の面積分はR→∞でゼロになるので
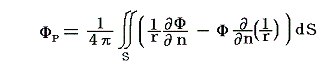
となり、物体の周りの任意の点の速度ベクトルは、運動物体の表面におけるΦと(∂Φ/∂n)が与えられれば求めることができることになる。
このとき、別稿3.(4)5.で注意したように、定常・非定常にかかわらず連続の方程式には時間tがあらわに含まれていないので各瞬間の境界条件が決まれば瞬時に流れの様子は決まり時間的な遅れはない。境界条件が時間的に変化する場合には流れも時間的に変化するが、縮まない流体の音速は無限に大きいため境界条件の変化は瞬時に流れ全体に伝わり、その瞬間の境界条件で流れが決まるからです。そのため、その瞬間の境界条件が同じなら、その瞬間の速度ベクトル場は定常・非定常に関わらず同じになります。つまり、物体の周りの速度ベクトル場はその瞬間の境界の位置と、その瞬間の境界の速度だけに依存し、その物体が過去にどのような速度であったかには関係しない。物体の過去の速度は物体の加速度に関係するのだから、流れの様子は物体の加速度には依存しない。[ただし圧力場は(∂Φ/∂t)を含むために過去の速度に依存します。]
[補足説明1]
しかしこのとき、(∂Φ/∂n)は運動物体の表面に垂直な速度成分だから運動物体の動きが定まれば完全に定まるが、境界面におけるΦを完全に決めることはできない。各瞬間の境界面におけるΦを決めるには境界面に沿った方向の流れが決まっていなければならない。ここで仮定しているような完全流体では摩擦ゼロで物体表面上を滑ることができるが、実際は摩擦のために境界面のごく近くの流体は物体表面に張り付いて物体表面とともに移動する。そのため境界面付近に大きな速度勾配を持つ境界層が形成され、境界条件のΦは完全には決定できない。実際の流れがどのようになるか決めることはできないのです。そのため流体力学では以下の様に考える。
3.渦列の取り扱い
一般に静止した状態から出発した流れは常に渦無しの流れとなる。しかし渦なしの流れにおいても、ごくわずか存在する粘性のために境界層ができ、また境界層が物体からはがれて、物体背後の止水域へ進むと止水領域との境に渦層を生じそれは孤立した渦となり渦列が生じる。
そのようにして渦なしの流れの中に渦列が生じるのですが、この状況で定まっている速度ベクトル場も上記の考え方に従うだろう。つまり物体の運動の結果生じる渦列の存在こそ上記の運動物体の境界層の働きを体現しており、その渦の存在が境界面Sにおける境界条件そのものだといえるだろう。
そのとき渦列は、流体が持つ粘性により物体の境界面から発生するのですが、一旦生じた渦は物体の境界面から離れた後、水や空気などの中ではなかなか消えない。それは水や空気は粘性が小さく粘性が無視できるからです。だから流体は完全流体として取り扱かう。
一方、流体力学の運動方程式から得られる「密度が圧力のみの関数になる完全流体(粘性がない)が(重力の様な)保存力のもとに運動する場合、最初に渦が無かったら永久に生じない、また最初に渦が存在したらその渦は消滅することなく流体とともに移動して永久に存在し続ける」というラグランジュの渦定理が成り立つので、一旦生じた渦は永久に保存されて、渦度は特異点として存在し続ける。実際の流れでは、ごくわずかな粘性の作用によって、孤立した領域の中で渦定理が破れて渦度が発生する。このような粘性の作用の典型的な例が、固体境界面に沿う境界層の領域であり、この境界層が剥離して流れの中に生じる渦層であり、この渦層が自ら巻き込んで形成される孤立渦です。
そのとき、他の大部分の領域では渦無しの状態が保たれると考えて、孤立した有限の渦度領域を伴う完全流体の流れを考える。つまり、上記の境界面の代わりとして渦列を用い、それ以外の部分は渦なしの流れが成り立つ粘性のない完全流体[非圧縮性なので発散=0]の流れを議論をしようと言うわけである。これが渦の理論で用いられる考え方です。
粘性によって渦が生じるのに、渦が生じた後には粘性のない流体として議論するというのは、何ともしっくりこない所ですが、数学的取り扱いが極めてやっかいな流体力学ではこういったやり方でやるしか無いのです。
(2)複素関数論
1.正則関数
複素関数論においては、複素数z=x+iyを変数とする複素関数w=f(z)は一般にwを実数部φと虚数部ψにわけて
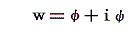
と書かれるのですが、このφとψはともに複素変数zの実数部xと虚数部yの関数です。すなわち
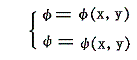
となります。
このとき、さらに複素関数w=f(z)の連続性と微分可能性が議論できます。複素関数の変数zに関する微分係数[あるいは導関数]は、実数関数と類似の式
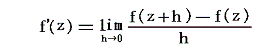
で定義されまする。ただし、ここで重要なことは複素変数zは実数軸と虚数軸で構成される平面[Gauss平面]上の二次元的な変数なので、微少変分hをゼロに近づける[つまりz+h→zにする]近づけ方はzの周りのいろいろな方向からのものが考えられます。そのため複素関数論では、どの方向からh→0としても、上記の微分係数が同じ値になる場合に微分が定義できるとします。ここが実数関数の微分積分学と非常に違うところです。
そして、ある複素変数域内の全ての点に於いて、f’(z)が存在するとき、関数f(z)はその変数域内において正則(regular)といい、このような関数を正則関数(regular function)[解析関数(analytic function)とも言う]と言います。正則という言葉を作ったのは、実数関数の微分の意味と少し違うので、それと区別するためだと思います。実際問題として実数関数の殆どのものに微分係数が定義でき、微分が定義できる関数が重要なのですから、複素関数においてもそのようなものをregular
functionと言って、それらを主に取り扱うのは妥当です。
上記意味において微分可能な関数を正則関数と言うのですが、複素関数が正則である必要十分条件がコーシー・リーマンの微分方程式
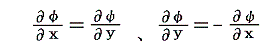
を満足することです。つまりコーシー・リーマンの微分方程式を満たす関数の組φとψを組み合わせた複素関数w=φ+iψは正則関数であり、上記の微分係数を持ちます。
このことは数学的に証明できます。実際、ある点において微分係数が存在すれば
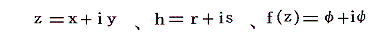
と置き、hが実数軸に平行に0に近づくとすれば、h=rとして
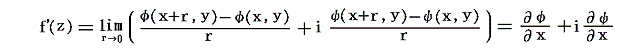
となる。次にhが虚数軸に平行に0に近づくとすれば、h=isとして
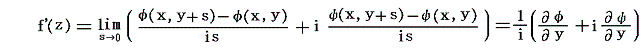
となる。微分係数はh→0の近づき方に無関係であるから
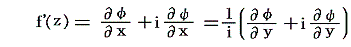
となる。従って
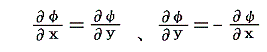
が得られ、コーシー・リーマンの関係式が成り立つ。
逆にコーシー・リーマンの関係式が成立すると
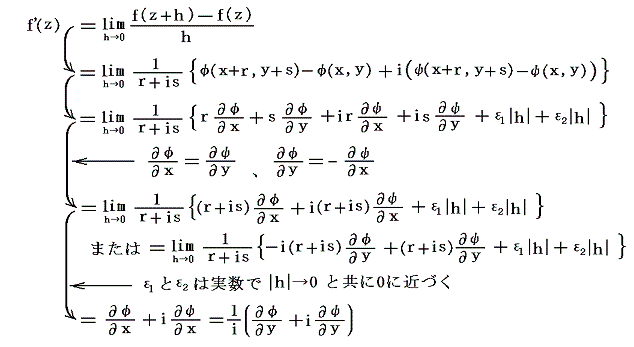
となり、微分可能が言える。
つまりコーシー・リーマンの微分方程式が成り立つことが正則関数であることの必要十分条件です。
ここで、φ(x,y)とψ(x,y)が第二次まで連続な偏導関数を持てばコーシー・リーマンの微分方程式の両辺をさらにx,yで偏微分して
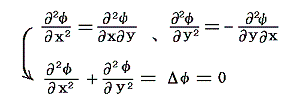
同様にy,xで偏微分して
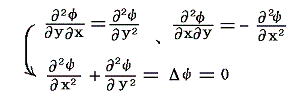
が得られる。つまりφもψもラプラスの方程式を満たす調和関数です。
2.複素速度ポテンシャル
別稿4.(2)2.で述べたように二次元・非圧縮性・渦成しの流れについては、変数(x,y)に付いての関数である速度ポテンシャルΦ(x,y)と流線関数Ψ(x,y)に付いてコーシー・リーマンの関係式
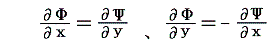
が成り立ちます。
3.(2)1.で述べた複素関数論におけるコーシー・リーマンの微分方程式は、上記の二次元・非圧縮性・渦なしの流れにおける速度ポテンシャルと流線関数についてのコーシー・リーマンの関係式と全く同じです。それならば、二次元流体力学の変数(x,y)を複素平面上の複素変数zの実数部xと虚数部yだと解釈し、速度ポテンシャルφ(x,y)と流線関数Ψ(x,y)を、複素関数w(z)=φ(z)+iψ(z)の実数部と虚数部と考えて議論できることになります。
この様に複素関数w(z)を構成すると、w(z)はzの各点で微分可能な正則関数となります。そのため、次の関係式が成り立ちます。
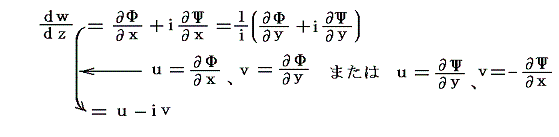
ここで、u(x,y)とv(x,y)は言うまでもなく座標(x,y)に於ける流体の速度ベクトルのx成分とy成分です。そのためwを複素速度ポテンシャル、dw/dzのことを共役複素速度と呼ぶことにしましょう。共役を付けたのはu+iv[これを複素速度と呼ぶ]に対して共役な関係[虚数の符号が反対]にあるからです。共役複素速度は、当然のことながら、速度の大きさをqとしx軸と速度の方向とのなす角θとすると
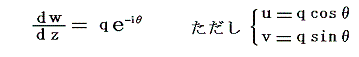
と表されることになります。
任意の正則関数w(z)を選ぶと、それの実数部Φと虚数部Ψは必ずコーシー・リーマンの関係を満足するからw(z)を複素速度ポテンシャルとするような二次元・非圧縮性・完全流体の渦なしの流れは必ず存在する。そのときz=x+iyとw=Φ+iΨの間の写像関係をうまく使うことによって様々な境界を持つ流れの様子を知ることができる。
[補足説明1]
正則関数の性質に関しては数学的に詳しく研究されていますので、その成果がそっくり利用できるのは大変なメリットです。今後、正則関数の性質を幾つか用いますが、複素関数論になじみのない方は適当な本を2,3冊読まれることを勧めます。
(3)複素関数を使った渦糸の表現
1.流線関数と速度ポテンシャル
例として2.(3)2.で説明した直線状渦糸を取り上げる。

このとき、別稿2.(2)で説明したように非圧縮性流体が連続の方程式を満足する場合には、常に流線関数(流れポテンシャル)Ψが存在する。そのため、上記の速度場は流線関数Ψを用いると
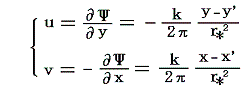
と表される。これを積分して、任意の付加定数を省略すると流線関数は
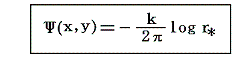
となる。
一方、同じく別稿4.(2)1.で説明したように、渦無しの領域では速度ポテンシャルΦが存在して、上記速度場は
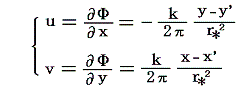
と表される。ただし、ここではgradの前の負符号-をとった形でΦを定義しています。負符号をつけるのは、Φをポテンシャルの山と考えて速度ベクトルが山を転がり落ちる方向を向くとした方がイメージしやすいからであって、それ以上の意味はない。そのため以後は-をとった形で定義する。だから速度ポテンシャルの山を駆け上がる方向が速度ベクトルの方向となります。[注意!!]
上記の連立微分方程式は直ちに積分できて
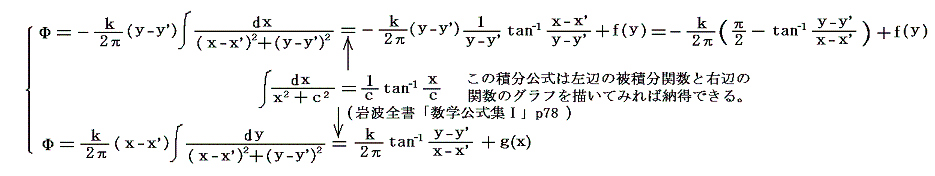
となる。積分定数を適当に調整すると速度ポテンシャルは
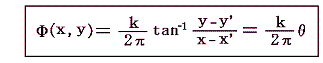
となる。ただし、θは位置ベクトル(x-x’,y-y’)とx軸が成す角度です。
2.複素速度ポテンシャルと共役複素速度
前節で求めたΦ(x,y)とΨ(x,y)はコーシー・リーマンの微分方程式を満足していました。そのため、これらを前記の複素速度ポテンシャルw(z)の実数部と虚数部とすることができます。つまり

となる。これはきわめて重要な結論です。
正則関数の和も正則関数となりますが、これは調和関数の解に対して重ね合わせの原理が適応できることに対応しています。そのためxy平面に垂直で互いに平行な直線状渦糸が同時に幾つか存在する場合の流体運動の複素速度ポテンシャルは次のようになります。これらの渦糸がxy面と交わる点をz1=(x1,y1)、z2=(x2,y2)、z3=(x3,y3)、・・・とし、強さをk1、k2、k3、・・・とすれば、任意点z=(x,y)に於ける複素速度ポテンシャルは
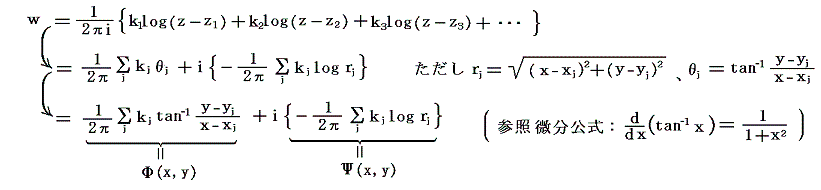
となる。ただし、ここでは流体は無限に広がり、かつ無限遠では静止しているとしている。
そのとき、任意点z=(x,y)に於ける速度のx成分は上記速度ポテンシャルwの実数部Φをxで偏微分[または虚数部Ψをyで偏微分]したものであり、y成分は虚数部Ψをxで偏微分して負符号をつけたもの[または実数部Φをyで偏微分したもの]になる。それは言うまでもなく、3.(3)1.の結論を加え合わせて求めた
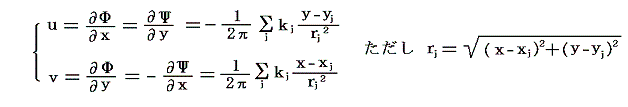
と同じものです。
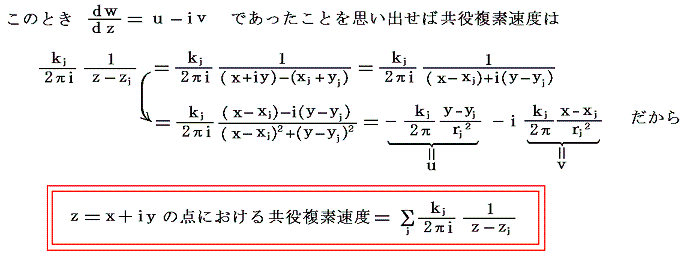
となる。
[補足説明1]
連続的な渦度分布を持つ渦領域は流れによって変形を受ける。そして、その変形はまた渦度が誘起する速度場を変化させる。このような連続的な渦度領域を伴う流れを一般的に取り扱うことはきわめて困難ですが、連続的な渦度分布を孤立した渦糸の集団によって近似すれば、渦糸系の運動としてある程度一般的に考察することができる。
(4)渦糸系の運動
1.渦糸系の中心
渦糸はその断面がきわめて細いものであるから、各渦糸は、他の渦糸によってその部分に誘導される速度を持って動くと考えて良い。従ってi番目の渦糸の持つ速度成分は

となる。ただしΣ’の’はj=iなる場合を加算から除くことを意味する。そのようにするのは、渦糸は自分自身に対しては速度を作り出さないからです。
このとき各渦糸の強さを、各渦糸の速度成分に乗じて加え合わせると、符号が異なるものが一度ずつ出てきて互いに打ち消し合うので
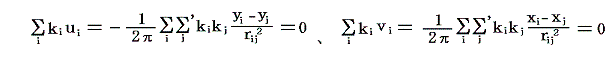
となる。このとき

なる座標値を渦糸系の中心と言うことにすれば
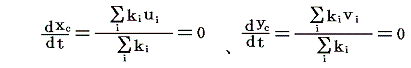
が常に成り立つ。渦糸系の中心とはkiをあたかも質点の質量の様に考えたときの重心の座標に相当するようなものであるが、そのような渦糸系の中心の座標はたとえ各々の渦糸が動いても不動である。
ここで次のことに注意してほしい。渦糸系の中心の座標は不動だと言っても、そこに存在する流体の速度がゼロであることを意味するのではない。この当たりはとてもわかりにくいところですから次節4.(1)の例を検討してください。
2.渦糸系の回転モーメント
次式によって、原点のまわりの渦糸系の回転モーメントを定義する。

ここで、(ui,vi)はi番目の渦糸の移動速度ベクトルであって位置ベクトルriの位置の流体の速度を意味するのではないことに注意。kiを質点の質量とみなすと、Mは質点系の角運動量に相当する様な量であると考えることができる。
このとき
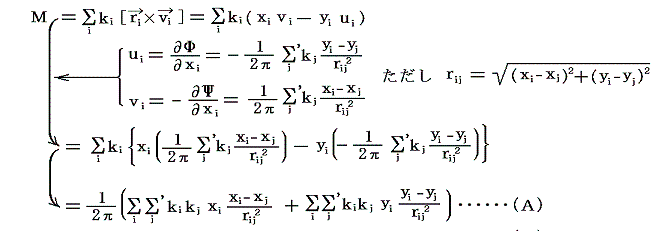
が成り立つ。ここで i と j の役割を入れ替えると、全く同様な式が得られる。
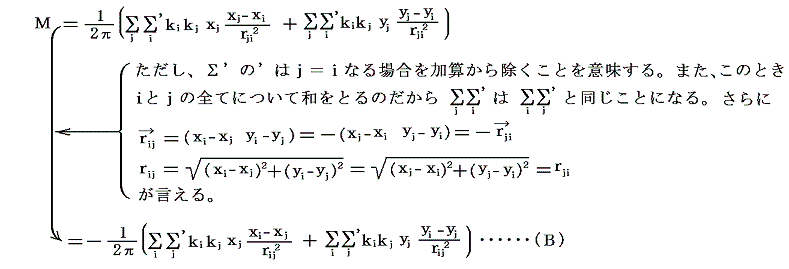
が成り立つ。(A)式と(B)式の辺々を加え合わせると
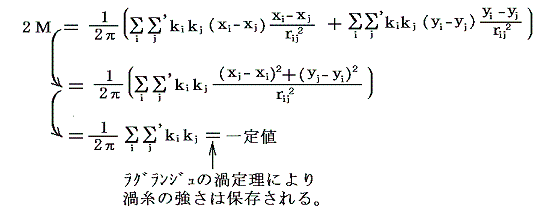
となる。
ここで原点は任意の場所に移動できるから、任意の固定点の周りの渦糸系の回転モーメントMは時間的に不変であることが証明できた。
4.渦列の例
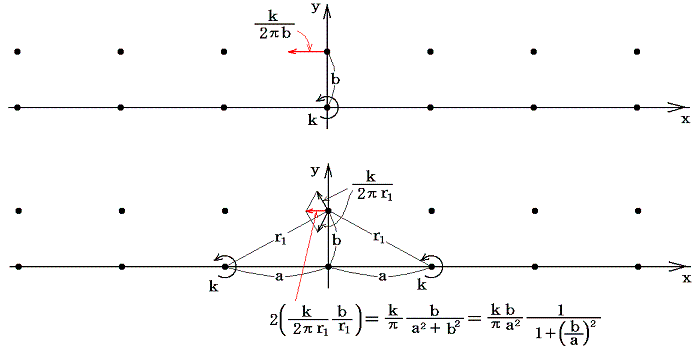
(1)二本の渦糸(k1+k2≠0の場合)
一番簡単な渦糸系の例として、渦糸が二本だけ存在する場合を考察する。まず最初に、渦糸がA、Bの二点に存在し、それぞれの強さがk1、k2でしかもk1+k2≠0の場合を考察する。
1.渦糸系の運動
二つのある瞬間の渦糸AとBの距離をdとすれば、渦糸AはBのためにAB線に垂直にq1=k2/(2πd)の大きさの速度を持ち、また渦糸BはAのために、AB線に垂直な方向にq2=k1/(2πd)の大きさの速度を持つ[下左図参照]。
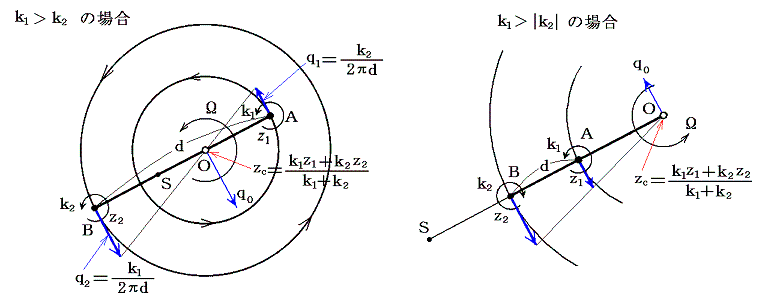
上左図において二つの速度ベクトルの先端を結ぶ線分と結合線ABが交わる点をOとする。そのとき、q1と線分OA、q2と線分OBを二辺とする二つの三角形は相似であるから点Oを中心として渦糸AはOAを半径とした円運動を、渦糸BはOBを半径とした円運動を行う。この中心Oは不動点であり、線分ABをk2:k1に内分する点です。これが前節で述べた渦糸系の中心です。渦糸AとBはこの周りを角速度Ωで回転する。そのとき角速度Ωは

の関係を満足するので、
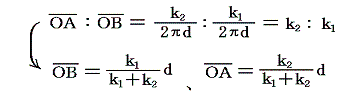
であることを考慮すると
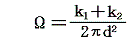
が得られる。ここで注意してほしいことは回転中心O[渦糸系の中心]の位置は変化しないが、その位置にある流体は速度q0で移動していることです。その速度は線分ABに垂直で大きさは
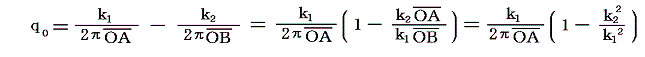
となる。
ならば、流体の速度がゼロとなる点はどこにあるのかと言うと、その点をSとする明らかに
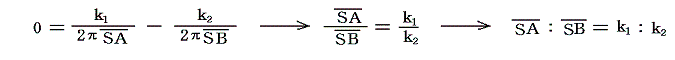
であるから、線分ABをk1:k2に内分する点であることが解る。ただしここで、次のことに注意しなければならない。その瞬間にたまたま点Sにいる流体の速度がゼロなのであって、次の瞬間には流体の速度がゼロとなる点Sは別の位置に移動していて別の位置の流体の速度がゼロになる。すなわちS点は点Oを中心としOSを半径とした角速度Ωの回転運動で移動していく。この当たりは次節の図の上で確認してください。
上左図はk1とk2が同符号でk1>k2の場合であったが、k1とk2が異符号でk1>|k2|の場合は上右図のようになる。
2.複素速度ポテンシャル
前記の結論を複素速度ポテンシャルの図示で説明する。強度2kの渦糸Aが(x1,y1)=(0,a)に、強度kの渦糸Bが(x2,y2)=(0,-a)に居る瞬間の複素速度ポテンシャルを求める。
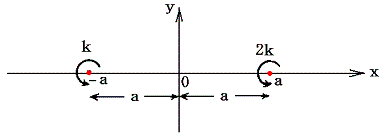
3.(3)2.の結論を利用すると

となる。
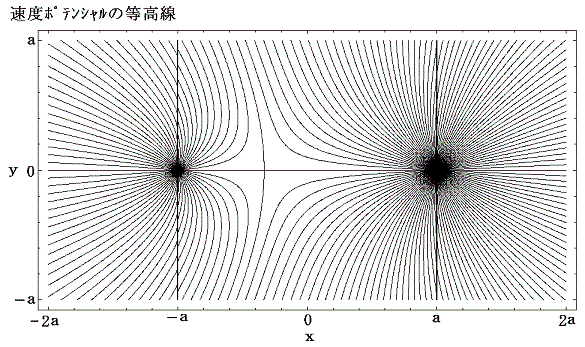
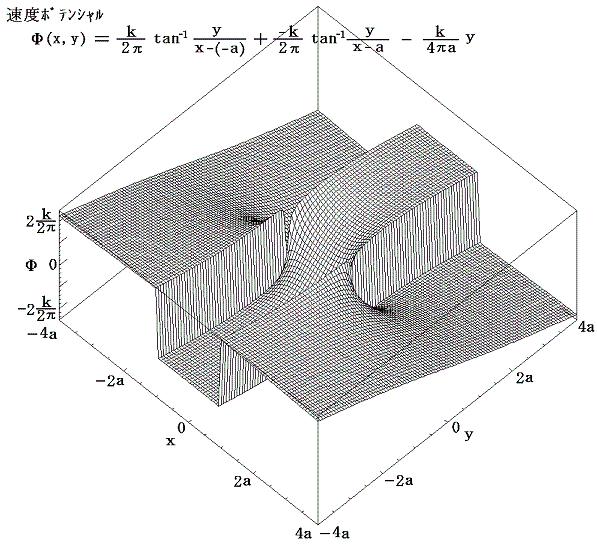
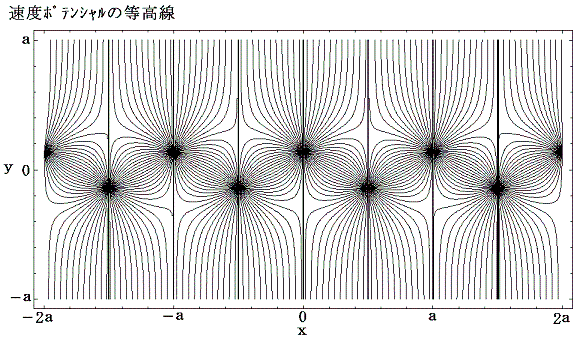
式処理ソフトMathematicaを用いて速度ポテンシャルを図示すると

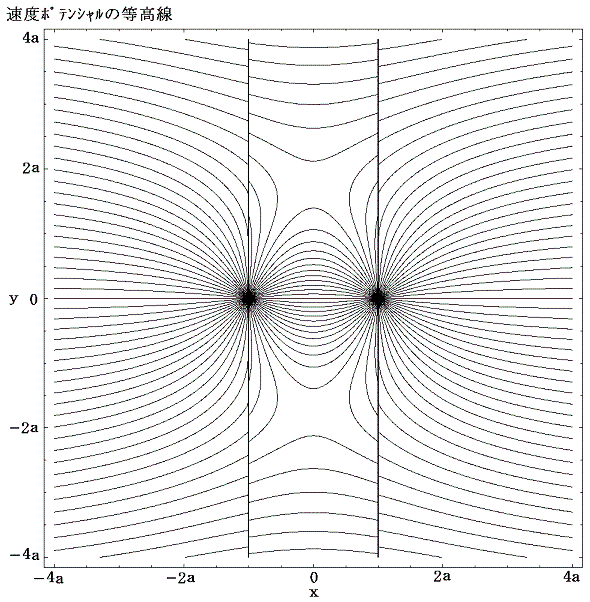
となる。この関数はx=±aの直線部分で不連続になるが、速度ポテンシャルで重要なのはその勾配であって、大きさの違いは問題ない。速度ベクトルは上図の速度ポテンシャルの山の勾配をさかのぼる方向を向き、下図の等高線に垂直である。
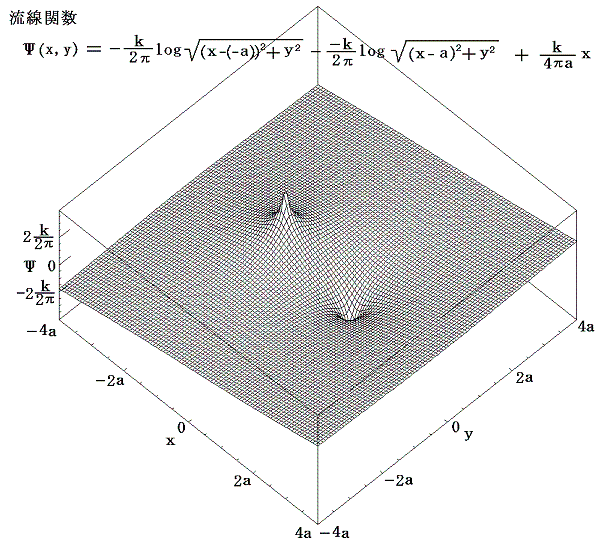
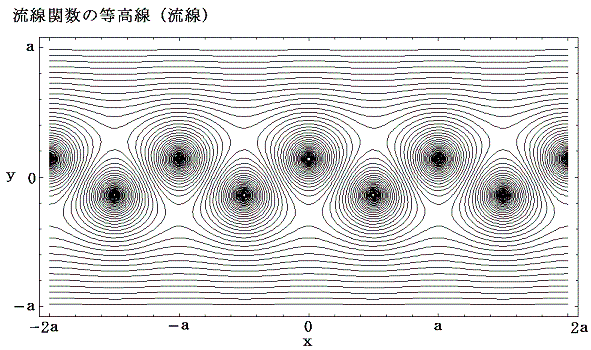
一方、流線関数のグラフは
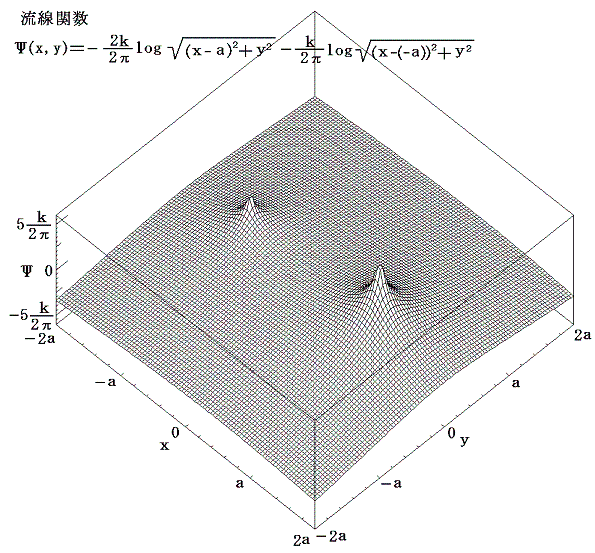
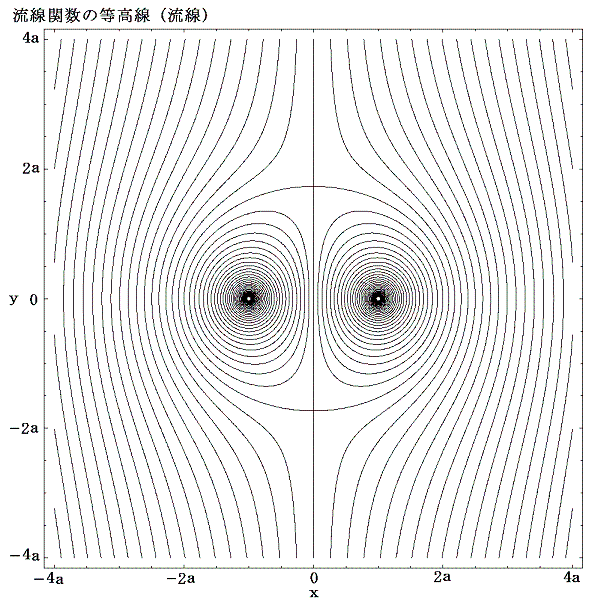
となる。流体は上図の流線関数の山を左側に見るように、下図の等高線に沿って流れる。等高線の標高差は以下特に断らない限り(k/2π)×0.1としています。
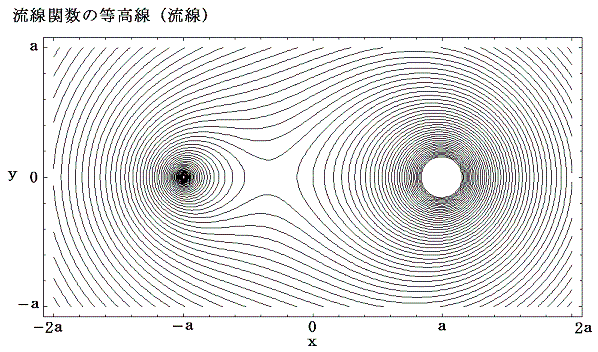
これらの図は前節の説明にうまく対応している。[異符号の場合の図は省略]
[補足説明1]
ここで是非注意してほしいことですが、速度ポテンシャルも流線関数も時間tをあらわに含んでいませんが、この流れは非定常流で速度ポテンシャルも流線関数も時間と共に変化します。実際前節4.(1)1.で述べたようにそれらはO点を中心にして回転していきます。
このようなことになったのは、渦なしで非圧縮性流体の場合連続の方程式に時間tがあらわに含まれないからです。もともとのコーシー・リーマンの関係式は非圧縮性流体の連続の方程式と渦無しの仮定から導かれたことを思い出してください。この当たりは別稿「二次元・非圧縮性・完全流体の力学(ラグランジュの渦定理とは何か)」3.(4)5.で説明しておりますのでそちらをご覧ください。
また、別稿2.(3)で述べたように非定常流では、実際に流体粒子が移動していく流跡線は流線とは異なっていることに注意。
(2)渦対(k1+k2=0の場合)
二本の渦糸A、Bの強さがk1=-k2の場合を渦対と呼ぶ。
1.渦対の運動
この場合にはk1+k2=0であるから、渦糸系の中心は有限の位置には存在しない。この場合には渦糸A、BはともにAB線に垂直な方向にq=1/(2πd)なる速度で動く[下左図]。
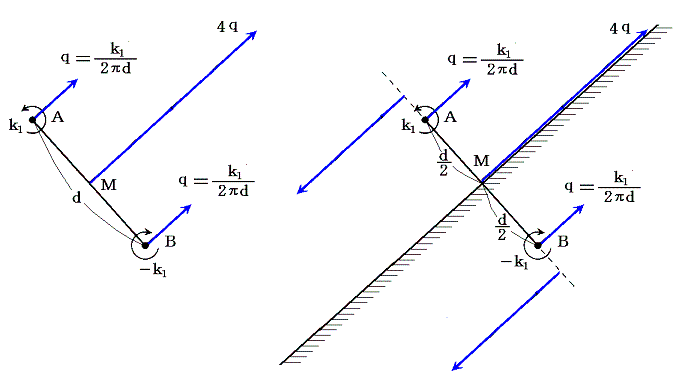
このとき、ABの中点は渦糸AとBの作用により4qの速度で同じ方向に動いていく。そして線分ABの延長上にある点では流体は渦糸AやBと相反する方向に流れる。 このとき中点MのみならずABの垂直二等分線の全ての点において、渦糸AとBにより生じた合成速度はこの垂直二等分線に平行になる。ただしその大きさはMから遠ざかるにつれて小さくなる。この流れは垂直二等分線に沿っており、これを剛体壁と考えると、剛体壁で要求される境界条件[法線方向の速度が0]を満足する。したがってこれを剛体壁で置き換えることができる[上右図]。
そのため、孤立して始め静止していた渦糸が壁に近づくと壁に平行に動き始める。しかも近づけば近づくほど速度は大きくなる。渦糸は、あたかも壁を鏡として自分自身を映した鏡像によって動かされるように動いていく。
2.複素速度ポテンシャル
前記の結論を複素速度ポテンシャルを図示して確かめてみる。強度kの渦糸Aが(x1,y1)=(0,-a)に、強度-kの渦糸Bが(x2,y2)=(0,a)に居る瞬間の複素速度ポテンシャルを求める。3.(3)2.の結論を利用すると

となる。
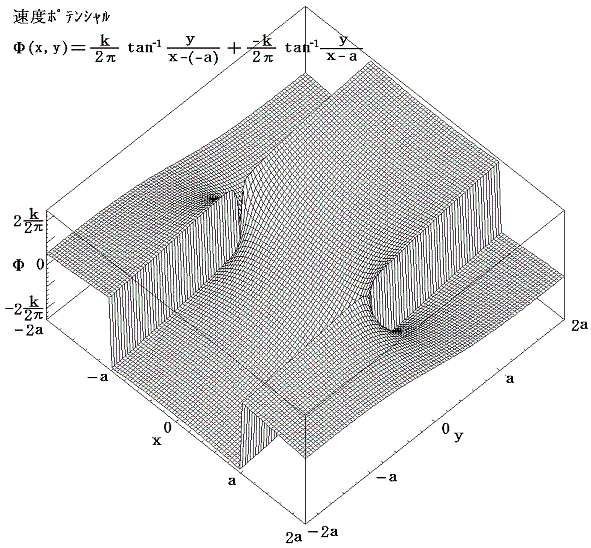
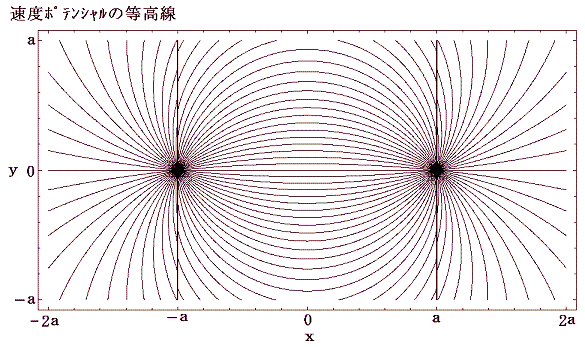
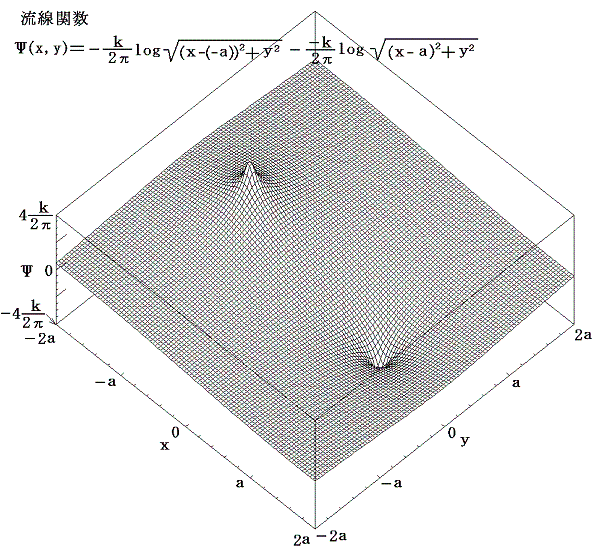
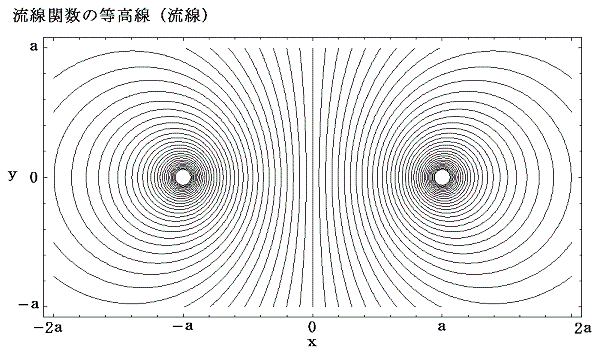
この場合y軸が鏡像線となる。また流線の間隔の狭いところが流速の早いところですから、流体の速度は渦糸対から離れるにつれて減少し、やがてゼロに近づく。この場合も非定常流なので流体粒子が移動していく流跡線は上図の流線とは異なっている。
3.渦対とともに動く座標系から見た場合
この場合も非定常な流れなので流線と流跡線が一致せず、流れの様子が非常にわかりにくい。流線と流跡線が一致する定常流にするため、渦糸対に固定した座標系から見た速度ポテンシャルと流線関数に変換してみる。そのためには上記の速度ポテンシャルΦ(x,y)、流線関数Ψ(x,y)に、y軸の負の方向へ一様な速度v=-k/(2π(2a))で流れる場を表す速度ポテンシャルΦ*、流線関数Ψ*
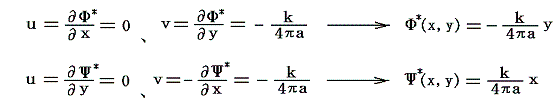
を重ね合わせればよい。そうすると
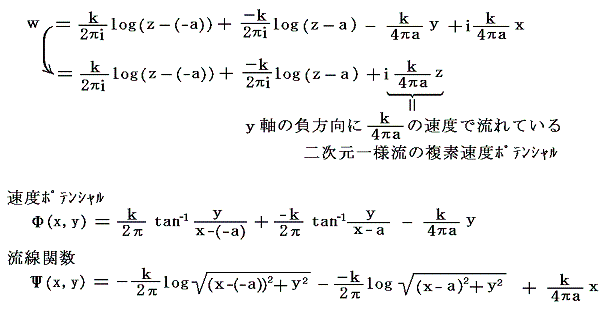
となる。渦糸対に固定した座標系から見た流れの様子は下図の様になる。実際はこのような流れの場が時間と共にy軸の正方向に速度k/(4πa)で進んでいく。
この図に於いてy軸から少し離れると、流線はy軸に平行で一定の間隔になる。その間隔はy軸の負の方向へ一様に流れる速度k/(4πa)に対応する。
渦対はお互いに協力してその前方にある流体を両サイドにかき分けながら進んで行くのである。そのとき渦糸系から少し離れると流体はほとんど影響を受けずに静止の状態にあると言って良い。前節の複素速度ポテンシャル図からは渦糸の影響が無限の彼方まで及んでいる様に感じるが、当節の図を見れば渦糸の影響は限られた領域であることと、渦が流体物質に付随しており、渦の動きにつれてその流体部分も移動していくことがよくわかる。実際こちらは定常流の中に静止している渦対の周りの流線であり、その場合の流線は実際の流体粒子の移動していく流跡線に一致していると考えることができる。
二本の渦糸の両端がつながってリンクを形成した場合が別稿で述べた空気砲の渦輪です。次図は回転しながら静水中を上昇していく渦輪の写真です。色素を巻き込んだその形が、二次元と三次元の違いはあるが上述の理論的考察の流線[流脈線]の形を見事に表示している。右側は下の渦輪が上の渦輪に追いついてその中心を突き抜けた瞬間の写真です。

[補足説明1](2013年9月追記)
渦についての興味深い記述。フィリップ・ボール著「流れ」早川書房(2011年刊)より引用
(1)二次元双極渦の挙動 説明文 実験写真
(2)木星大赤斑のメカニズム 説明文1 説明文2 説明文3 観測・実験写真
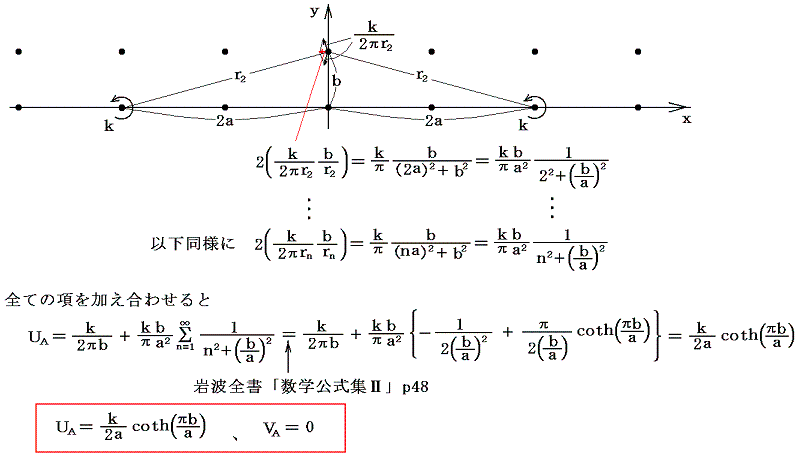
(3)直線上に等間隔で無限に並んでいる渦糸系
等しい強さkの渦糸が一直線上に等間隔aで並んでいる場合を考える。
1.複素速度ポテンシャル
この直線をx軸にとり、各渦糸の座標を下図の様にとる。
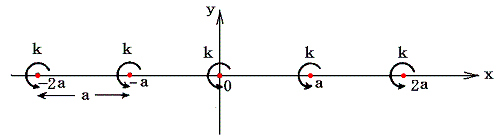
このときz=(x,y)なる位置における複素速度ポテンシャルは3.(3)2.で説明した結論を用いると
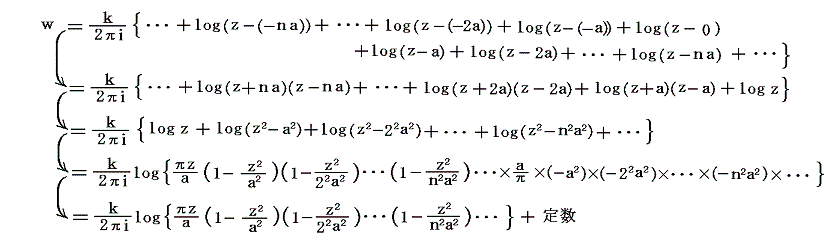
となる。ところで複素速度ポテンシャルはその微分値のみが重要で付加定数は意味を持たない。そのため付加定数を取り除いたものを改めて複素速度ポテンシャルとすると

となる。これを実数部と虚数部に分けると
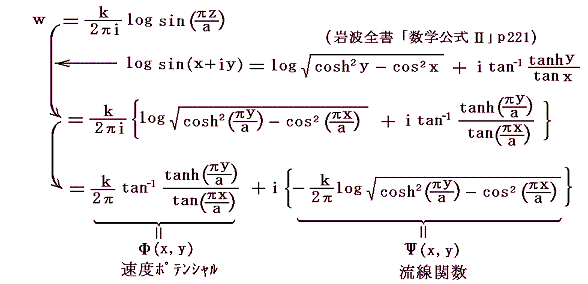
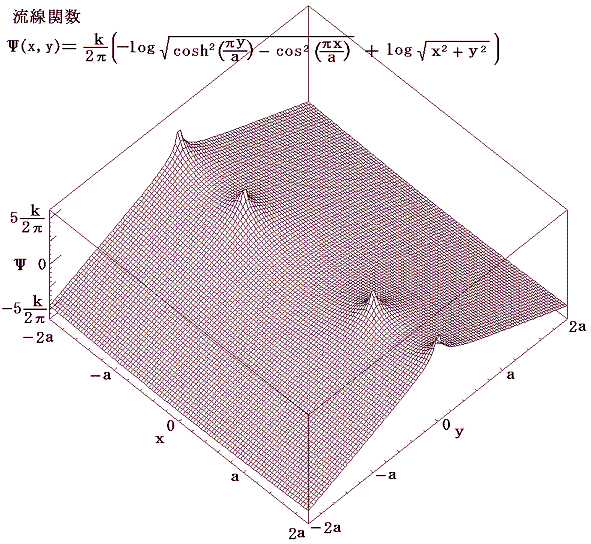
2.速度ポテンシャルと流線関数
前節の関数を数式処理ソフトMathematicaを用いてグラフ表示する。
速度ポテンシャルのグラフは
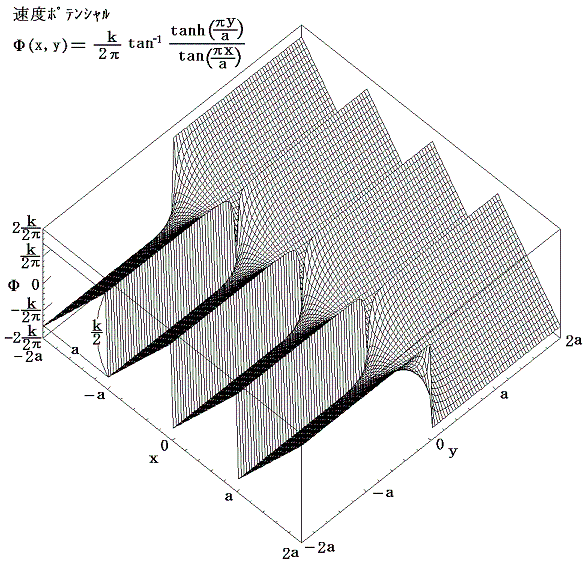
となる。速度ベクトルは上図の速度ポテンシャルの山の勾配をさかのぼる方向を向き、下図の等高線に垂直である。
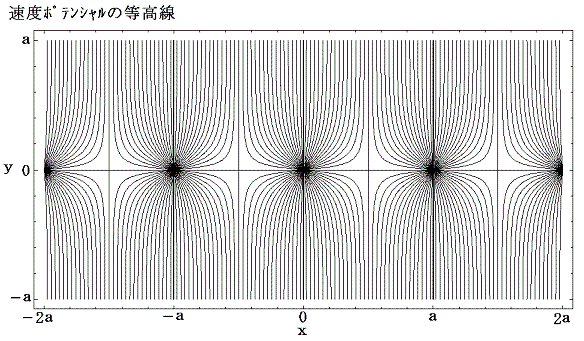
流線関数のグラフは
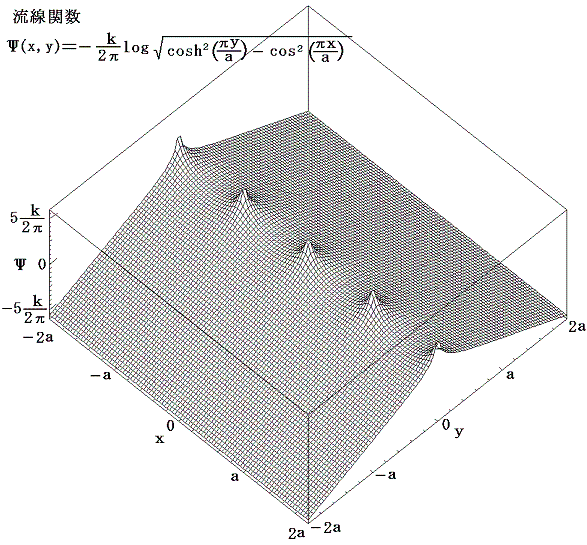
となる。流体は上図の流線関数の山を左側に見るようにして、下図の等高線に沿って流れる。

3.共役複素速度
z=x+iyにおける共役複素速度u-ivは速度は
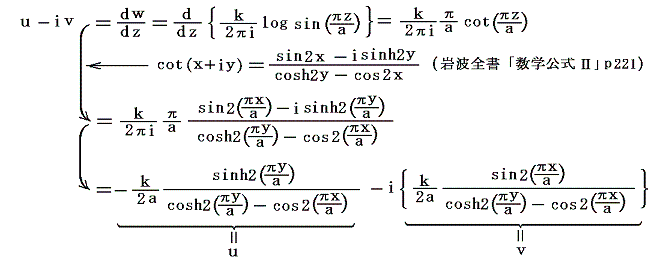
となる。複素関数の微分が上記の様になることについては、複素関数論の教科書を参照されたし。
ここで双曲線関数のグラフは
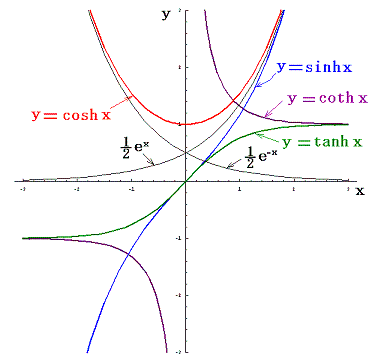
の様になることを考慮するとy→+∞の位置の速度ベクトルは(u,v)=(-k/2a,0)、y→-∞の位置の速度ベクトルは(u,v)=(k/2a,0)となる。つまり渦列の上方では左向きに、下方では右向きの一様流となる。大局的に見れば、渦糸列は互いに反対向きに流れる二つの一様流の間の渦層と同等になる。これは1.(1)で述べた事情に対応します。
4.一直線上に並ぶ渦糸系の安定性
一直線上に等間隔で並ぶ渦糸系の安定性を調べてみる。たとえば原点z=0の位置に生じる共役複素速度u0-iv0は3.(3)2.と3.(4)1.で説明した様に上記のw(z)から原点の渦糸の速度ポテンシャルを差し引いた複素速度ポテンシャルw’(z)をzで微分して得られる関数のz=0における値で与えられる。

つまり、原点(z=0)における共役複素速度はゼロとなる。それは、渦糸が原点に対して左右対称に存在しており、x>0側の渦糸が原点に誘起する速度成分とx<0側の渦糸が原点に誘起する速度成分が互いに反対向きで打ち消し合うためにそのようになるのである。渦列は無限に並んでいるから、原点を他の渦糸の位置に移動すれば全く同じことが言える。つまり一直線上に等間隔で無限に並んでいる同じ強さの渦糸列はその場所に静止している。
それはまた、前節までの議論から明らかなように、複素速度ポテンシャルw’の実数部分の関数Φ’(x,y)の(x,y)=(0,0)における勾配で表されると言っても良い。

速度ポテンシャルと流線関数を図示すると以下のようになる。

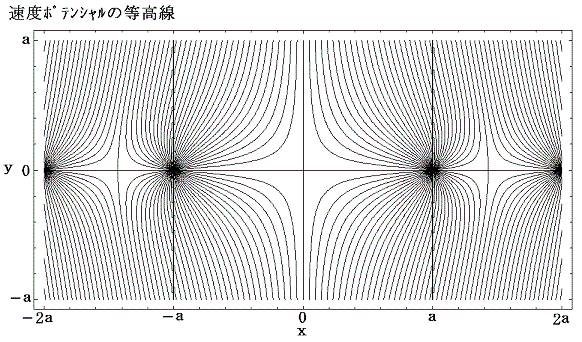
図から明らかなように速度ポテンシャルのz=0の点は鞍点(馬の鞍の様な形)となる。そのため原点に存在する渦糸は静止の状態にある。
しかしながら、渦糸の位置が原点からわずかでもずれると速度成分を持って移動していくことが解る。ここでの速度ポテンシャルの定義では速度ベクトルはポテンシャルの最大勾配をさかのぼる方向を向くのだから、その位置がxy座標の第二象限、第四象限にずれると時間と共に原点からますます離れていく。また第一象限と第三象限にずれると一旦は原点方向へ移動するがその後やはり原点から外れていく。この当たりは前記の共役複素速度の原点付近での近似式からも読み取れるし、次の流線関数の等高線で表される流線からも読み取れる。
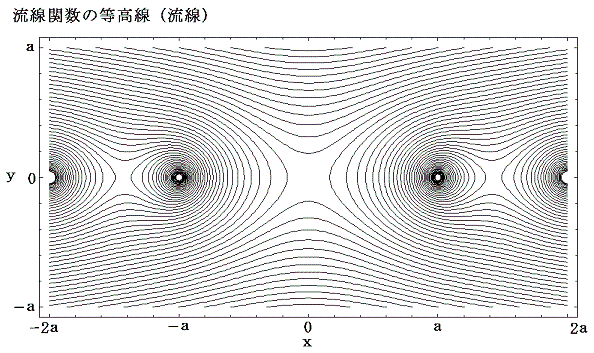
渦糸は無限に並んでいるのだから、原点を他の渦糸の位置にずらせば他の渦糸についても同様な事情が言える。つまり全ての渦糸は最初は静止の状態にあるが、その直線状の配列は仮に安定であるだけで僅かの攪乱により時間と共に散り散りに崩れてしまう。
5.カルマン渦列(静的考察)
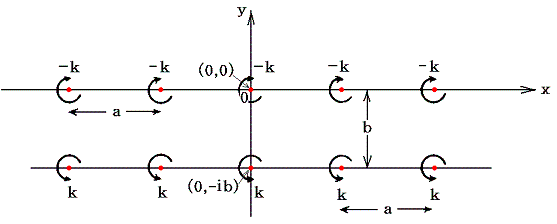
ここからいよいよカルマンの渦列の説明に入るのですが、このように複雑な現象を取り扱うには、いかに単純化したモデルを設定するかが大切です。カルマンは数学的に取り扱えるようにするため、考察に必要な最低限の要素を残して、極限まで単純化した。それは
- 渦の発生源(渦列は物体の後流に中に生じる)は無限遠にあり、その存在を無視できる。
- 渦の列は無限に長い真っ直ぐな渦列をなす。
- 二つの渦列中の渦は等間隔で並んでいる。
- すべての渦の強さは等しく、二つの渦列の回転方向は逆向き。
- 渦が動く方向は渦列の方向と一致している。
というものです。この中で、特に重要なのは仮定5です。
カルマンはこのような仮定をした上で渦列の安定性を調べた。上記の条件を満たす渦の配列は沢山考えられるが、安定な配列は以下に述べるタイプAかBしか無く、一般的なタイプCは安定ではないことが直ちに判明する。できるだけ直感的に理解できるように、最初は複素関数論を使わずに説明します。
(1)初等的な説明
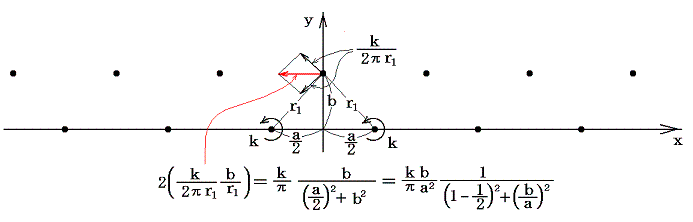
1.向かい合う配列
下図のように渦がそろって並んでいる配列タイプAは安定です。
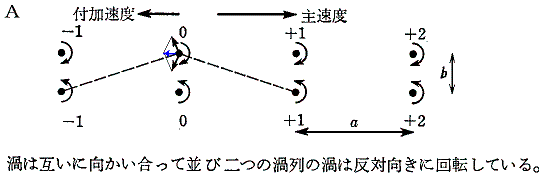
図の渦に-∞から+∞までの番号を付ける。そして、たとえば上列の渦0に注目する。
このとき、上列渦0は上列両隣の上列渦±1からは速度の増加に対して何の寄与も受けない。その理由は、渦の運動学の法則により、着目渦に誘導される速度は、その原因となった渦と結ぶ直線に垂直で、方向は原因渦の回転方向だからである。この法則により、上列渦+1と-1から上列渦0に誘導される速度は相殺される。同様に上列渦+2と-2から誘導される速度も相殺される。以下同様で上列渦からの寄与はすべて相殺されてゼロになる。
下列渦0からは、上列渦0を列に沿って負の方向へ向かわせる速度が誘起される。斜め向かい側の下列渦+1と-1の作用も上列渦0を列の負の方向に向かわせる速度を誘起する。下列渦+2と-2の組み合わせの場合も同様である。以下同様で、無限個並んでいる下列のすべての渦の効果を足し合わせた無限級数は有限な値に収束する。
渦は無限個並んでいるとしているので、着目する渦を他の渦に変えても全く同様な結論が得られる。そのため渦列はその配列を保ったまま、すべての渦を付加速度UAで左方に動かすことになる。下側の渦列についても同様で、上側の渦列と同じ付加速度UAで左方に移動する。そのため渦全体の配列は安定に保たれる。
2.互い違いの配列
下図のように二列の渦列が互い違いになった配列タイプBも安定です。
この場合も下列渦0および下列渦1からの作用(図に点線で示してある)を始め、一般に下列渦-nおよび下列渦+(n+1)からの作用はすべて上列渦0に左向きの速度を誘起する。それらすべてを合成すれば上側の渦列を全体として負の方向へ向かわせる付加速度UBが再び得られる。
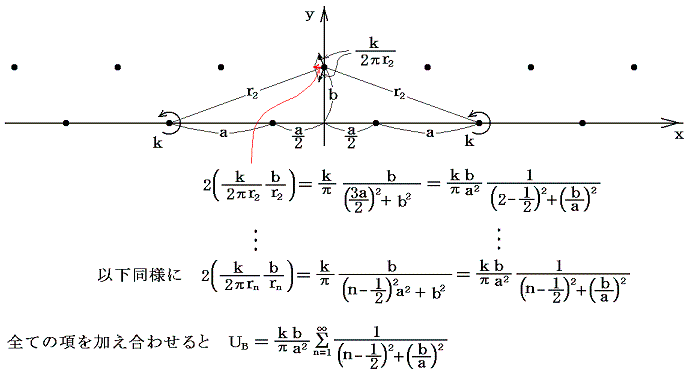
となるが、この和は次のように考えれば簡単に計算できる。
上図の赤丸と黒丸の渦列を合わせたものは、すでに求めたUAの結論のaをa/2とおいたものに等しい。そのためUBの和はUAのaをa/2に置き換えたものから、UAの結論を引いたものに等しい。そのため
となる。
下側の列の渦列についても同様で上側の渦列と同じ付加速度UBで同じ方向に移動する。そのため渦の配列は安定に保たれる。
3.任意にずれている配列
上下の渦列が任意にずれている配列タイプCは不安定です。

上列渦0に働く下列渦0と下列渦-1の効果を考える。上列渦0の周りに誘起される速度は、上列渦0-下列渦0間と上列渦0-下列渦+1間の距離と方向が対称的でないため、誘起速度は原因渦からの距離の増大とともに小さくなることを考慮すると、上列渦0を列に対して左斜め上に移動させる効果を生じる。その他の組み合わせについても同様である。そのためこの配列は最初の仮定を満足できない。
(2)複素関数論による説明
初等的には前節のように説明できますが、複素関数論を使えばもう少し詳しいことが解ります。
1.複素速度ポテンシャル
座標軸を下図の様に取る。
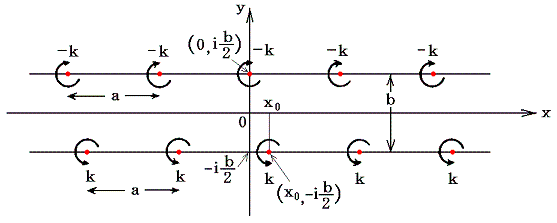
この二列の渦糸系による点z=x+iyにおける複素速度ポテンシャルw(z)は4.(3)1.と同様にして
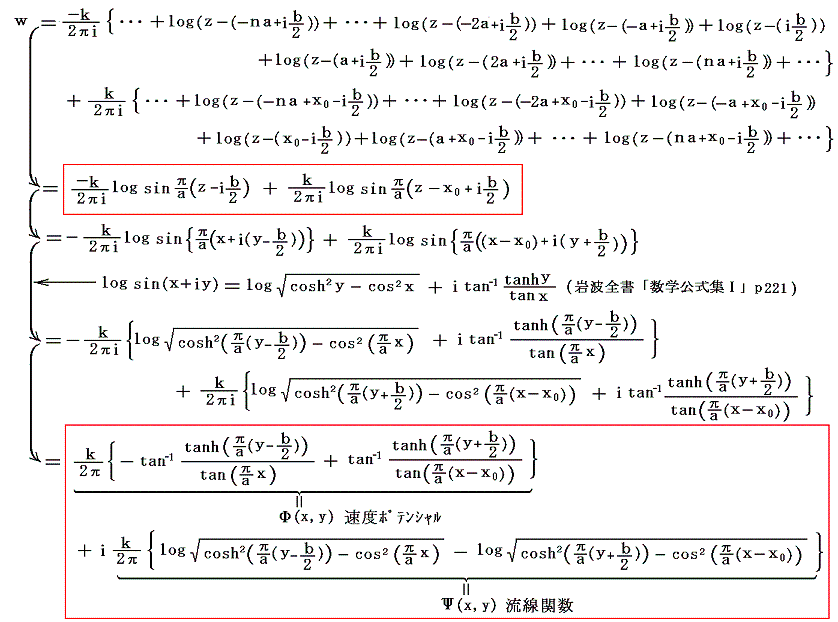
となる。
2.共役複素速度
最初に点z=x0-ib/2に存在する渦糸の位置の共役複素速度を求める。4.(3)4.で見たように、渦糸系がただ一列存在する場合は動かなかったから、たとえばz=x0-ib/2の点の渦糸に対してy=-ib/2の位置にある渦列の寄与はゼロとなる。そのためz=x0-ib/2にある渦糸に影響するのは、前記wから点z=x0-ib/2の渦糸を取り除いた複素速度ポテンシャルw’の前半部分[つまりy=+ib/2の位置にある渦糸列]だけです。そのためz=x0-ib/2点の共役複素速度は
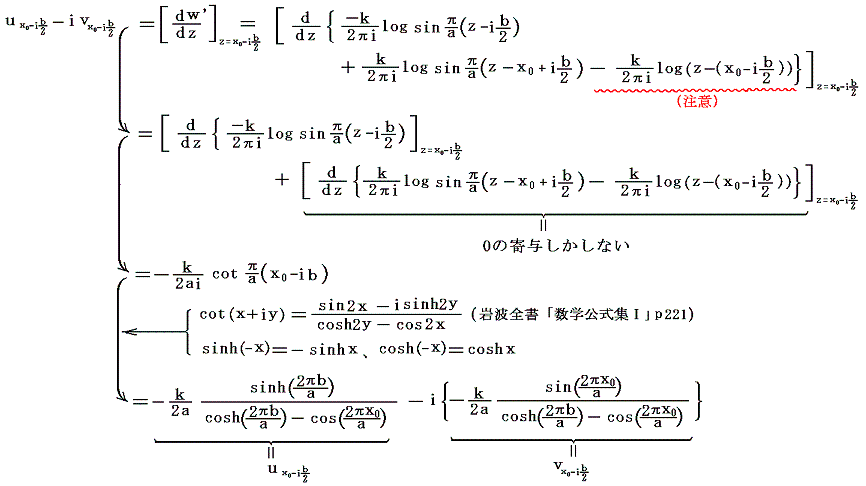
となる。渦糸は無限に並んでいるのであるから、下の列に関しては他の渦糸も全て同じ速度で動く。
同様にして、上の列のz=0+ib/2の点にある渦糸の共役複素速度は
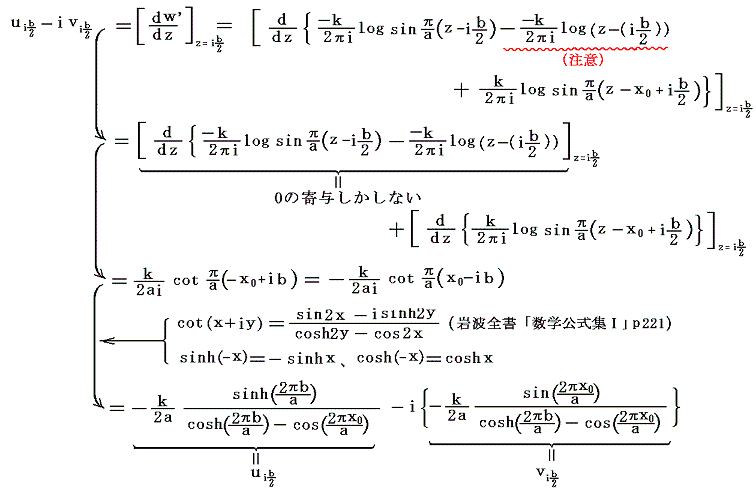
となる。つまり、上の渦糸も全てが下の列と同じ速度で動く。
以上の結論から、渦糸系全体はそのままの形を保ったままで斜めの方向へ動く。その移動方向はx軸に対する傾斜角をθとすると
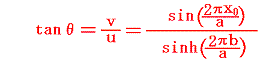
となり、上下渦列のずれ量x0に関係する。
それではいかなる場合に、渦糸系はその列に平行に動くかというと、v=sin(2πx0/a)=0が成り立つとき、すなわちx0=0またはx0=a/2のときです。これは前節5.(1)で述べたタイプAまたはBの場合です。そのとき渦列の移動速度はそこで求めた値と同じになります。
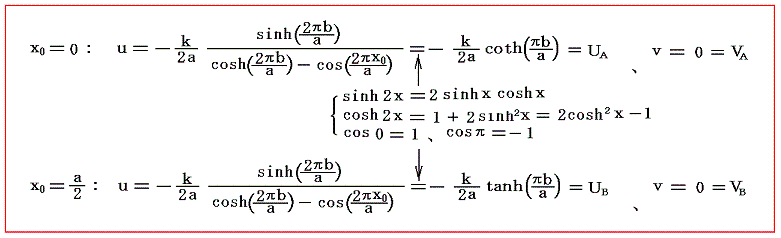
ただし、4.(3)4.で述べたのと同じ事情で、上記の安定性は仮のものであり、これが持続的に安定であるかどうかは動的な考察をしてみなければ解らない。
(3)流れの様子
動的考察に入る前に、流れの全体の様子を確認しておく。
1.共役複素速度
渦糸の位置以外の任意の点z=x+iyにおける共役複素速度は
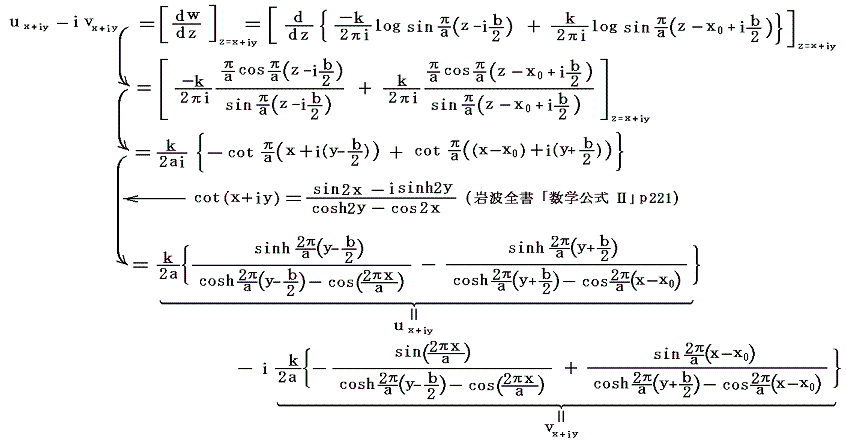
となる。
特に、x0=0(タイプA)とx0=a/2(タイプB)の場合を考察する。A、B両タイプとも二列の渦列の真ん中の層(x軸上のy=0である部分)は、平均的に左方向へ動いて行く。もちろん、その速度にはxの値の変化に伴う周期的変動はあるが、平均的大きさはA、B両タイプとも左向きにk/aである。[計算は省略]
またy→+∞、またはy→-∞となるにしたがって速度は急速にゼロに近づく。実際渦列から少し離れると流速はすぐにゼロに近づく。[計算は省略]
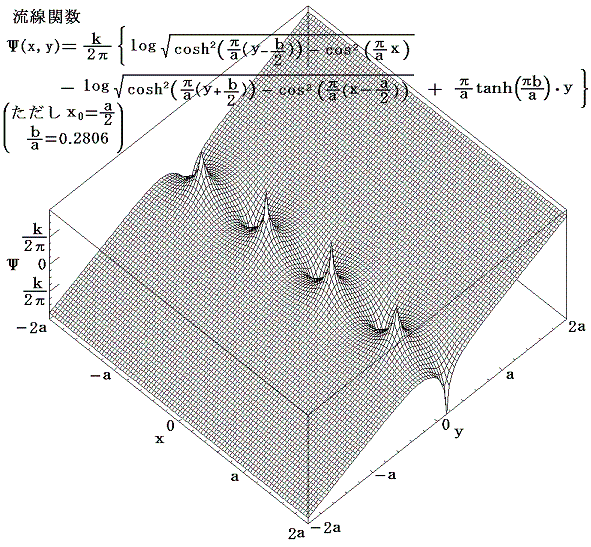
これらの事柄を、x0=a/2(タイプB)でしかもa/b=0.2806の場合のグラフにより確認する。
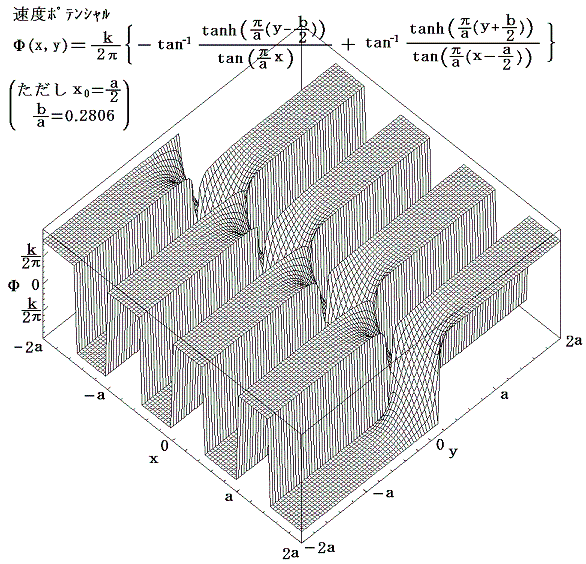
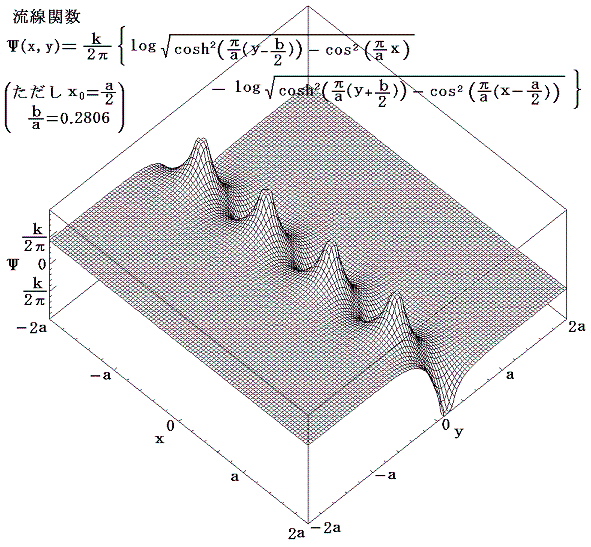
2.タイプB[x0=a/2]でしかも a/b=0.2806 の場合
これは次章で動的にも安定性な配列であることが確認されるものです。この場合の複素速度ポテンシャルは
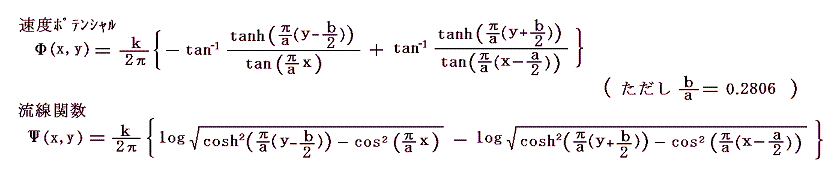
となる。
何度も注意しているように、ここでの定義では、速度ベクトルの方向は速度ポテンシャルの山をさかのぼる方向であり、流線は流線関数の山を左に見ながら流れる方向になる。
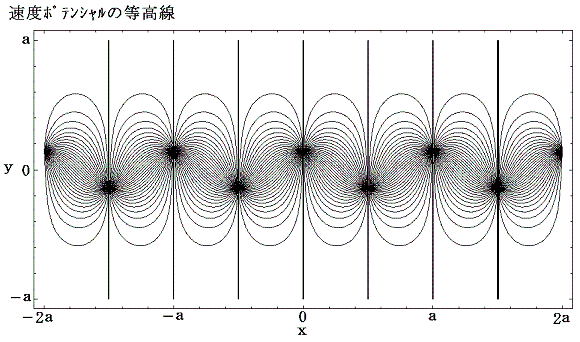
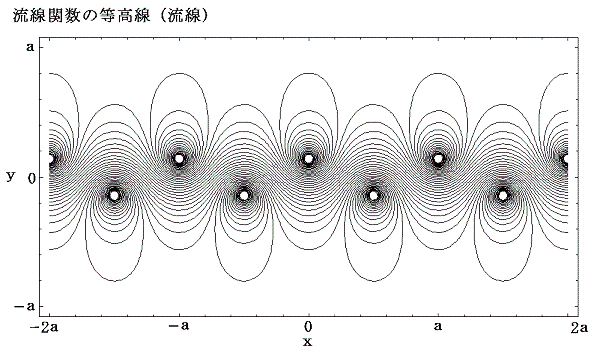
次の写真はレイノルズ数250で定常的に運動している円柱の後流における渦列を、水面に浮かべたアルミニウム粉末を写真撮影して可視化したものです。カメラは静止した流体に固定されている。

理論通りの流線が再現されていることが良くわかる。このとき渦列の外側では速度は急速にゼロに近づくことに注意されたし。また二本の渦列の間には平均すると左向きの流れが存在する。ただし、別稿2.(3)で注意したように非定常流では、実際に流体粒子が移動していく流跡線は流線とは異なっている。
3.タイプB[x0=a/2、a/b=0.2806]で渦糸に固定した座標系から見た場合
渦糸列に固定した座標系から見た複素速度ポテンシャルを図示してみる。そのためには上記の速度ポテンシャルΦ(x,y)、流線関数Ψ(x,y)に、x軸の正の方向へ一様な速度UB={k/(2a)}・tanh(πb/a)で流れる場を表す速度ポテンシャルΦ*、流線関数Ψ*
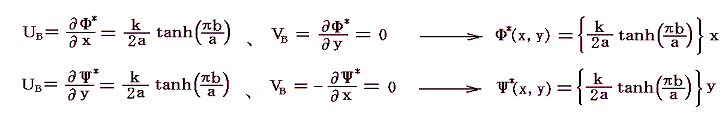
を重ね合わせればよい。そうすると

となるから、渦列に固定した座標系から見た流れの様子は下図の様になる。

上図の様子からわかるように、渦列の影響は渦列の近くに限られることが理解できる。渦列から離れたところの流線は、速度{k/(2a)}・tanh(πb/a)の右向きの流れを表す。また渦糸に固定された座標系からみても、二本の渦列の間には左向きの流れが存在することがわかる。
次の写真は円柱を水面に垂直に差し入れて動かし、水面に浮かべたアルミニウム粉末を、渦列と等しい速度UBでカメラを左方に動かしながら撮影したものです。上記の理論的な結論が実際の流れでもそのまま実現されているので、ここまでの理論的考察が大筋で間違っていないことが解る。

4.タイプB[x0=a/2、a/b=0.2806]で円柱に固定した座標系から見た場合
次に示す流線関数の等高線(流線)の様子はタイプB[x0=a/2、a/b=0.2806]の場合でしかも円柱がUBの7倍の速度で左方向に移動しているとして、動いている円柱に座標系を固定して渦列の様子を見た場合です。
円柱の速度と渦糸の速度比7:1は実際の速度比に即しています。また、この図では等高線の間隔を今までの図の5倍にしてあります。

次の写真はレイノルズ数250で定常的に運動している円柱の後流における渦列を、水面に浮かべたアルミニウム粉末を写真撮影して可視化したものですが、カメラは動いている円柱と同じ速度で左方に動いている。

この場合も理論の流線が良く再現されている。
済州島や屋久島の様な孤立峰の背後にできる季節風による雲の渦列はこの状況に付随した雲の様子を見ている事になります。
6.カルマン渦列の動的な安定性
5.章の静的な考察ではタイプAとBの両方が安定のように見えるが、実際の渦列ではタイプBしか生じない。その理由を明らかにするには渦列の配置に小さな攪乱を与えて、その攪乱がどのように変化していくかを動的に追跡する必要がある。つまり各渦の位置座標(xm,ym)や(xn,yn)をアトランダムに少しずらしたとき、注目する一つの渦の所に生じる付加速度が時間とともにどのように変化するかを計算してみるのである。
動的な安定性を考察することによってタイプAは不安定なことが解りますが、そのとき注目すべきはタイプBが安定であるためには、渦列の前後間隔aと列間隔bが特定の比率でなければならいことが明らかになることです。これはカルマンが得た成果の中でも最重要なものです。なぜならこの間隔こそ渦列が引き起こす共鳴振動の振動数に深く関係しており、それは様々な現象に重大な影響を与えるからです。
(1)タイプA
1.微小な攪乱
対称型渦列の配置に対して座標を下図の様に取る。
この渦列全体は前章で求めた速度UAで左方へ動くから、任意時刻tにおける渦糸系の座標は
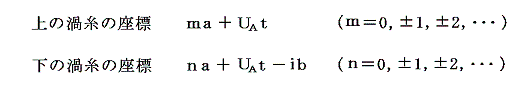
となる。今それぞれの渦糸に小さな変位zm、znを与えて
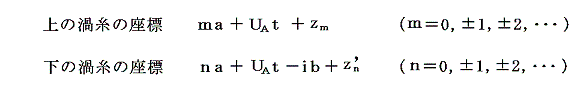
なる位置へ動かしてみる。このとき|zm|、|zn’|は最初は全て小さいものと仮定する。これらがいつまでも小さいままであれば渦列は安定であり、そうでなければ不安定であるということになる。
2.m=0の渦糸の共役複素速度
ここで上の列のm=0の渦糸の共役複素速度を
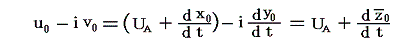
と表すことにする。ここで、x0、y0は原点にある渦糸の位置時刻tにおける座標値です。z0の上のバーは共役であることを明示するためです。
このとき、x0、y0の位置にある渦糸に対する上の列のm、-mなる二つの渦糸による共役複素速度、下の列のn、-nなる二つの渦糸のによる共役複素速度、およびn=0の渦糸によるよる共役複素速度は3.(3)2.より

となる。ここで、x0、y0の位置の自分自身の渦糸によるものは除いている。これらの式を二項定理で展開する。そのときz0、zm、z-m、zn’、z-n’は全てaやbに比較して微小な量と考えられるので、これらについての一次の項だけを残すと
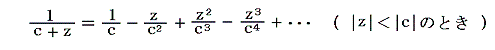
であるから

となる。
ここで微小変位をα、βを小さな複素数として、zm=αcos(mθ)、zn’=βcos(nθ)のタイプのものを考える。ここで0<θ<2πとする。もしθが小さいと、これらの攪乱は波長2πa/θの波動の性質を持つ。実際にはもっとアトランダムな攪乱を考えた方が良いのかも知れないが、そのようにしたのでは計算ができないので上記の様な攪乱で代用する。
実際の所、上記の波動状攪乱の周期はθを変えれば調整できので、θを変えたものを重ね合わせれば任意の攪乱を表現できる。だから任意のθ値に対して安定ならば、その配置が安定であると言って良いであろう。そのように考えれば上記の仮定は妥当なものだと言える。
z0=αcos(0×θ)=αであることを考慮し、b/a=γと書くことにすると、前記式は

となる。ここで
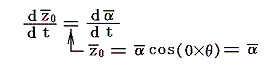
であることを考慮すれば、上の列のm=0なる渦糸の共役複素速度は
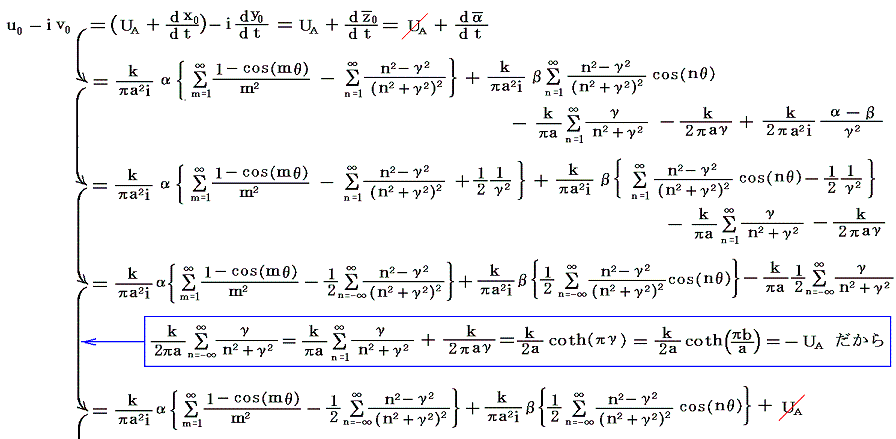

となる。
3.攪乱振幅αとβが満たすべき微分方程式
前節の結論を用いると攪乱の振幅αが満たすべき微分方程式として
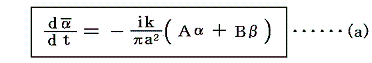
が得られる。
全く同様な手順で、下の列における任意の渦糸に対して
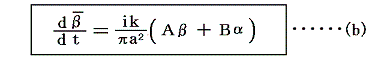
なる式を得ることができる。これは丁度(a)式のkを-kにして、αとβを入れ換えた式となっている。
ここでさらに、(a)式の共役な式として
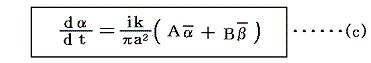
が得られる。
(c)式の両辺をtで微分して(a)、(b)式を用いれば
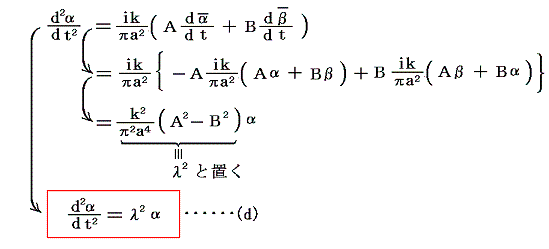
が得られる。微分方程式(d)の一般解はよく知られているように、D、Cを積分定数とすると

となる。
4.定数λ2の値
一般解(e)において、λ2>0ならばλは実数となり、αは時間と共に増大するので運動は不安定になる。一方、λ2<0ならばλは純虚数となり、運動は周期的になり、この配列は安定であることになる。
ところで関数
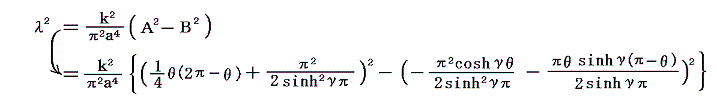
のθとγを変数としたグラフは下図の様になる。
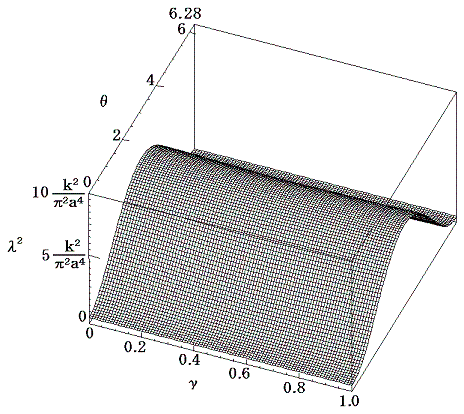

グラフから明らかなように、θとγのどの値の範囲でもつねにλ2>0となるのでλは実数となり、αは時間と共に増大するため、この配列の渦列は不安定である。
(2)タイプB
1.微小な攪乱
非対称型渦列の配置に対して座標を下図の様に取る。
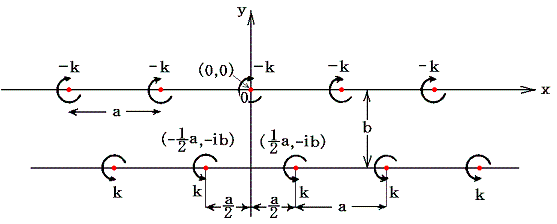
この渦列全体は前章で求めた速度UBで左方へ動くから、任意時刻tにおける渦糸系の座標は
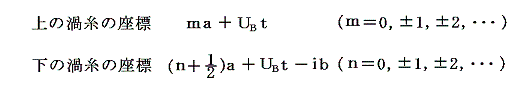
となる。今それぞれの渦糸に小さな変位zm、znを与えて
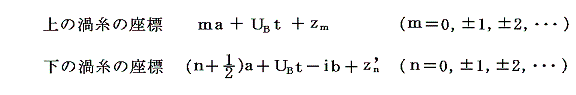
なる位置へ動かしてみる。このとき|zm|、|zn’|は最初は全て小さいものと仮定する。これらがいつまでも小さいままであれば渦列は安定であり、そうでなければ不安定であるということになる。
2.m=0の渦糸の共役複素速度
ここで上の列のm=0の渦糸の共役複素速度を
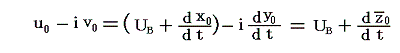
と表すことにする。ここで、x0、y0は原点にある渦糸の位置時刻tにおける座標値です。z0の上のバーは共役であることを明示するためです。
このとき、x0、y0の位置にある渦糸に対する上の列のm、-mなる二つの渦糸による共役複素速度、下の列のn、-n-1なる二つの渦糸のによる共役複素速度は3.(3)2.より

となる。ここで、x0、y0の位置の自分自身の渦糸によるものは除いている。これらの式を二項定理で展開する。そのときz0、zm、z-m、zn’、z-n’は全てaやbに比較して微小な量と考えられるので、これらについての一次の項だけを残すと
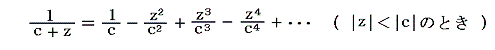
であるから

となる。
ここで微小変位をα、βを小さな複素数として、zm=αcos(mθ)、zn’=βcos(nθ)のタイプのものを考える。ここで0<θ<2πとする。もしθが小さいと、これらの攪乱は波長2πa/θの波動の性質を持つ。そのようにするのはすでに述べた理由による。
z0=αcos(0×θ)=αであることを考慮し、b/a=γと書くことにすると、前記式は

となる。ここで
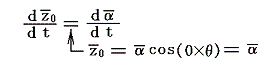
であることを考慮すれば、上の列のm=0なる渦糸の共役複素速度は
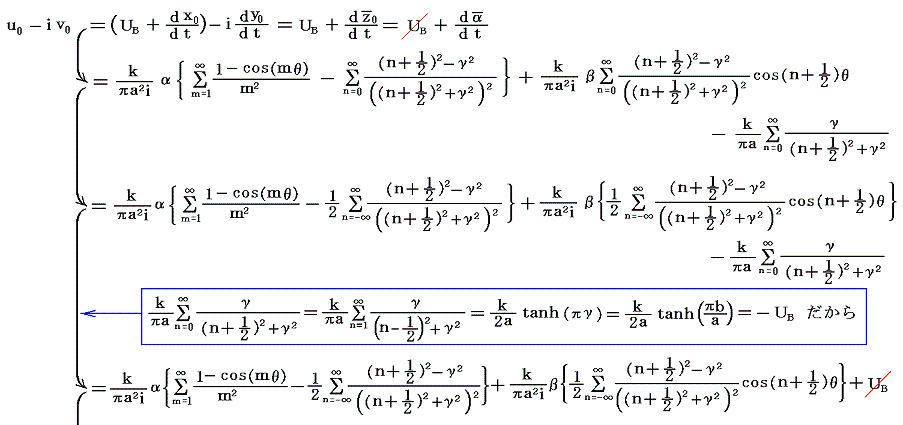

となる。
3.攪乱振幅αとβが満たすべき微分方程式
前節の結論を用いると攪乱の振幅αが満たすべき微分方程式として
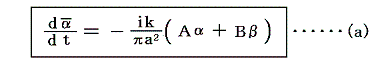
が得られる。
全く同様な手順で、下の列における任意の渦糸に対して
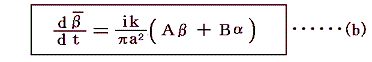
なる式を得ることができる。これは丁度(a)式のkを-kにして、αとβを入れ換えた式となっている。
ここでさらに、(a)式の共役な式として
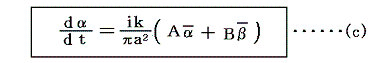
が得られる。
(c)式の両辺をtで微分して(a)、(b)式を用いれば
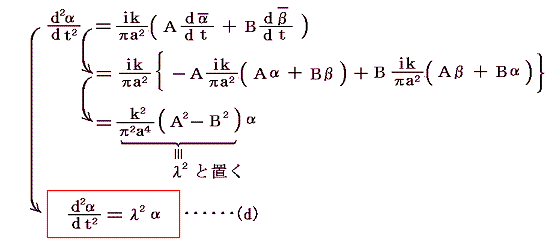
が得られる。微分方程式(d)の一般解はよく知られているように、D、Cを積分定数とすると

となる。
4.定数λ2の値
一般解(e)において、λ2>0ならばλは実数となり、αは時間と共に増大するので運動は不安定になる。一方、λ2<0ならばλは純虚数となり、運動は周期的になり、この配列は安定であることになる。
ところで関数

のθとγを変数としたグラフは下図の様になる。
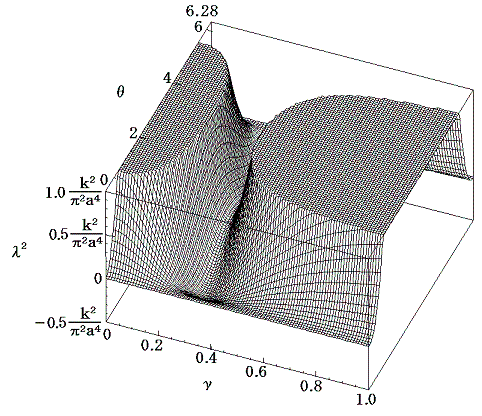
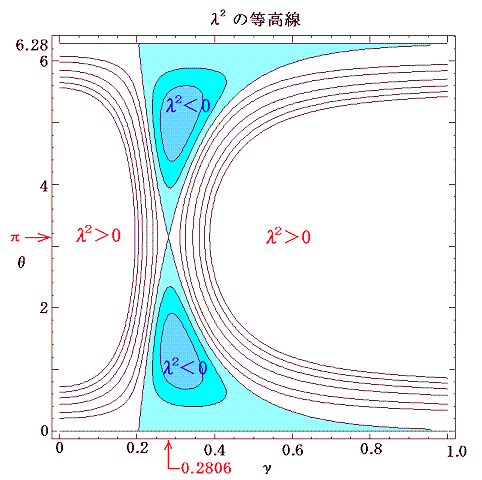
グラフから明らかなように、θが0~2πの任意の値を取るとき、渦列タイプBの配置が安定であるためにはγがある特定の値でなければならないことが解る。その特定値でのみθの値にかかわらず常にλ2<0が成り立つ。そのときλは純虚数となり、αは周期的な解となる。
その値は図から明らかなようにθ=πでλ2=0となるときのγの値です。θ=πのときBθ=π=0であるから、Aθ=π=0の条件から求めればよい。すなわち
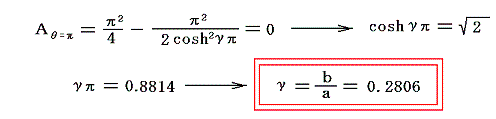
となる。これがカルマンが理論的考察によって得た値です。実際これは現実の現象とよく一致する。そのため、今日この配列の非対称渦列をカルマンの渦列という。
上記の値を用いると渦列の間隔a、渦糸の強度k、渦列の移動速度UBの間に成り立つ関係式
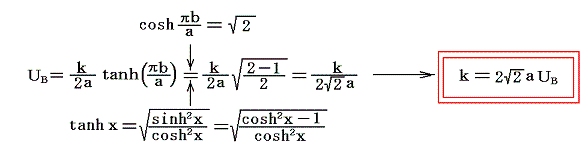
が導けます。これも重要な結論です。
(3)複素速度ポテンシャルによる安定性の検討
カルマンは上記のような計算をして求めたのですが、複素速度ポテンシャルのグラフを解析することによっても同様の結論が導けます。4.(3)4.で一直線上に無限に並んでいる渦列の安定性を、渦列の複素速度ポテンシャルw(z)から、着目する渦糸の複素速度ポテンシャルを差し引いた複素速度ポテンシャルw’(z)を用いて論じた。ここでも二列の渦列について同じことをやってみよう。
1.複素速度ポテンシャルw”
ここでは座標軸を下図の様に取る。
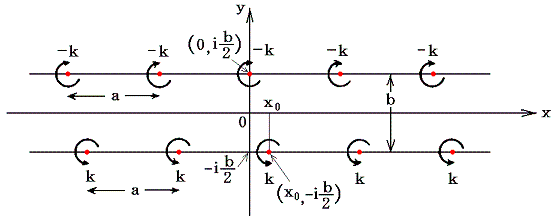
ここで位置z=0+i(b/2)の渦糸に働く共役複素速度u-ivは5.(2)1.で求めた複素速度ポテンシャルw(z)から、位置z=0+i(b/2)の渦糸の複素速度ポテンシャルを差し引いた複素速度ポテンシャルw’(z)をzで微分して得られる関数のz=0+i(b/2)における値で与えられる。

そのため、z=0+i(b/2)における渦糸が、その位置を安定に保つかどうかを調べるにはw’(z)に、5.(3)3.で導いたx軸の正の方向へ一様な速度UB={k/(2a)}・tanh(πb/a)で流れる場を表す速度ポテンシャルΦ*と流線関数Ψ*
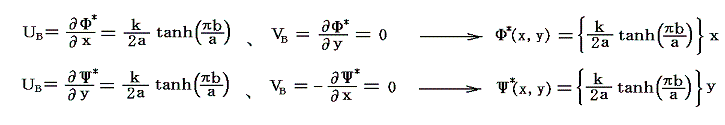
を重ね合わせたものw”(z)=Φ”(x,y)+Ψ”(x,y)の様子を調べればよい。つまり
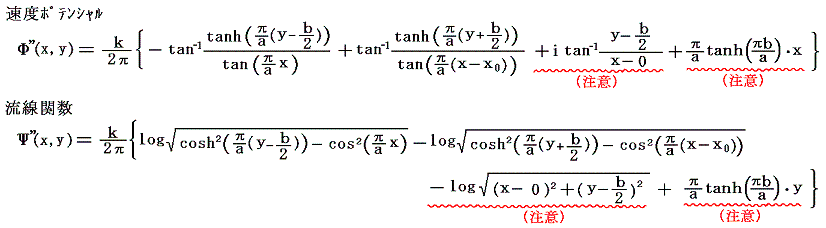
のグラフを、x0を0~a/2の範囲、またb/aの値を0~1の範囲で色々変えて描いてみて、その様子を調べればよいのです。数式処理ソフトをお持ちの方は是非実行してみられることを勧めます。
2.カルマン解のグラフ
色々描いて見れば直ちに明らかになるのですが、x0=a/2のタイプBでしかもγ=b/a=0.2806の場合のみ下図のようにz=0+i(b/2)の付近に安定領域が出現する。
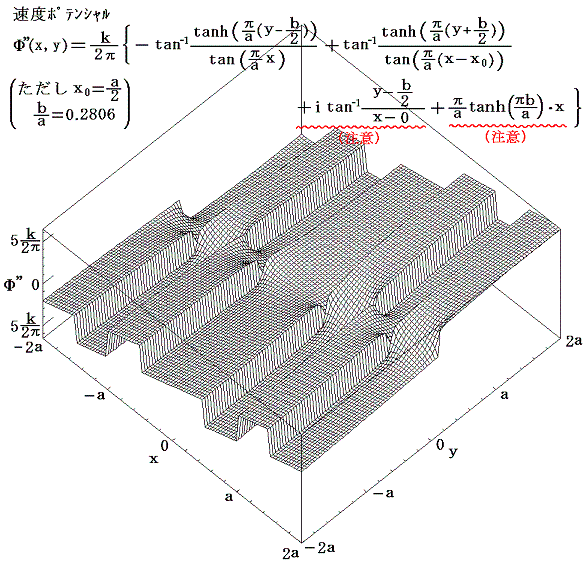
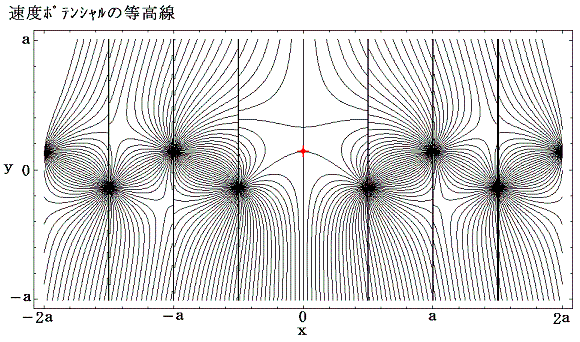
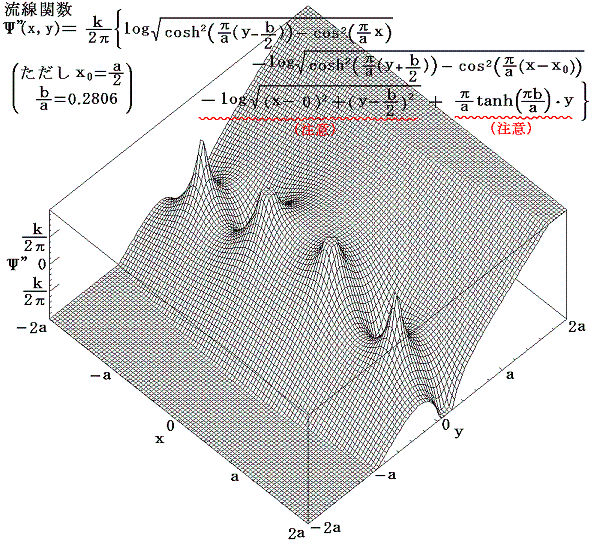
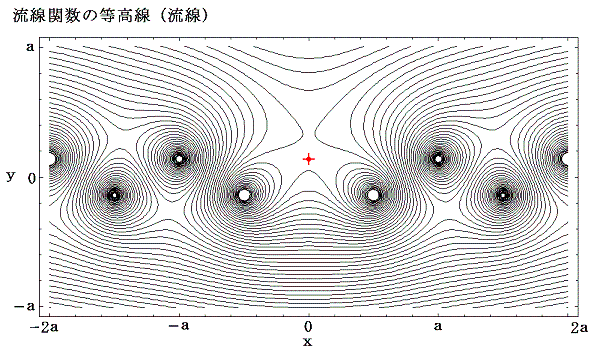
図中の+点近傍が安定領域となっていることに注目してください。
3.補足説明
なぜカルマン解の場合にのみ安定領域が現れるのかは、UBの速度場を加えていないw’(z)=Φ’(x,y)+Ψ’(x,y)のグラフを検討すれば了解できる。


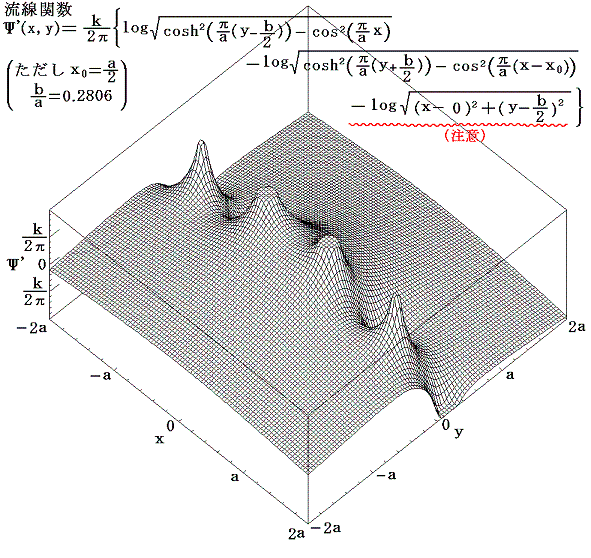
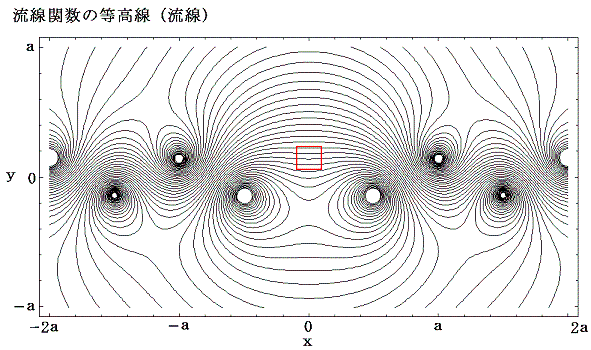
上図の□で囲った領域に着目してほしい。まずx0がa/2以外ではこの領域のポテンシャル面の傾きを図の方向にすることはできないことに注意。これがタイプAやCが安定配列になり得なえず、タイプBのみになる理由です。
さらにこの位置のポテンシャル面の勾配はγ=b/aの値が小さくなる[二列の渦列の距離を近づける]につれて急勾配になることに注意。つまりγ=b/a=0.2806にすると言うことは、この勾配の大きさがUBのポテンシャル勾配をちょうど打ち消すようになるまで二列の渦列を近づけると言うことです。これがγ=b/aが特定の値にならねばならない理由です。
カルマンはもう一つ重要な結論を導いています。それは
「渦によって運ばれる流体には運動量が付加されるが、これが柱状物体が流体中を進行するときに受ける抵抗に関係する。」
と言うものです。これも重要な成果ですが説明は別稿「渦抵抗(カルマン渦列と抗力)」に回します。
7.参考文献
カルマンの源論文をネット上でかなり探したのですが見つけることができませんでした。そのため、このHPは下記文献1~3に依存しています。
カルマンの渦列を解説した本やHPはたくさんあるのですが、渦列の配置を導く動的安定性の計算過程を詳しく紹介したものは少ない。若い頃読んだ文献2.にそれが説明されていたのを記憶していましたので、いつかこれを解りやすく説明するHPを作りたいと思っていました。しかし渦とその周りの流れをカルマンが行ったようなやり方で取り扱っても良いのだと言う確信がどうしても持てなかったのです。
そのため長い間棚上げ状態でしたが、退職して時間が取れましたので、2ヶ月間かけて若い頃に読んだ流体力学の教科書を読み直してみました。そしてやっとそのようにしても良い、いやそれ以外にやりようがないのだと納得できましたので作ることができました。その当たりは別稿「二次元・非圧縮性・完全流体の力学(ラグランジュの渦定理とは何か)」で説明しておりますのでそちらも併せて御覧下さい。
- Horace Lamb 著「Hydrodynamics」sixth edition、Cambridge University Press(1932年刊、初版は1879年刊)P224-229
Lambによるとカルマンの源論文は簡潔にしか書いてないので、彼はこの本で途中の式をかなり補ったと言うことですから、おそらくカルマンはこのように展開したのだろう。この本の内容のそのままが下記URLのpdfファイルで紹介されていますので参考にされてください。
http://www.phys.chuo-u.ac.jp/labs/nakano/tokuron1/sec8(tokuron1).pdf 「8カルマン渦列の不安定性}
- 友近晋 著「流体力学」共立出版(1940年)の文献社による復刻版(1972年刊)P224-244
私が探した限りでは、動的安定性の計算過程が日本語で読める唯一の本です。このHPの内容はこの本の記述に従っています。微小攪乱の置き方がLambの本と少し違っていますので方程式の形は少し違いますが結論は同じです。
- Arnold Sommerfeld 著「理論物理学講座 Ⅱ変形体の力学」(昭和44年刊)講談社 P253-263
ベクトル解析の基本定理[ヘルムホルツの定理]や渦列の安定性の静的な議論の所はかなり参考にしました。
- テオドール・フォン・カルマン著(谷一郎訳)「飛行の理論」岩波書店(1971年) P65-71
- テオドール・フォン・カルマン(リー・エドソン)著「大空への挑戦 航空学の父 カルマン自伝」森北出版 P65-68、230-234
これはカルマンの最晩年にライターの協力を得て書かれた本です。
ラグランジュの渦定理、グリーンの定理から始まってベクトル解析のヘルムホルツの定理、複素関数論と沢山の準備をして、得られた結果はγ=b/a=0.2806だけかと思われるかも知れません。しかし、はるばる議論して得られた結果が実際の現象をうまく説明するということは、ここまでに利用した様々な考え方や手法が、おそらく大筋に於いて間違っていないことを示している。
そう考えれば、ここに至る途中の過程で得られた成果こそが価値あるものだと言っても良いでしょう。
[2012年1月追記]
ある読者の方が、カルマン渦列の第一論文のpdfファイルを送ってくださいました。有名な論文なのでその内容を紹介します。これはカルマンが「飛行の理論」の中で解説している二つの論文の最初の方です。