�@���̃y�[�W�������������������̃o�[�W�����������p�������B�u���E�U�[�ł͌��ɂ����̂ł�������͑N���ł��B
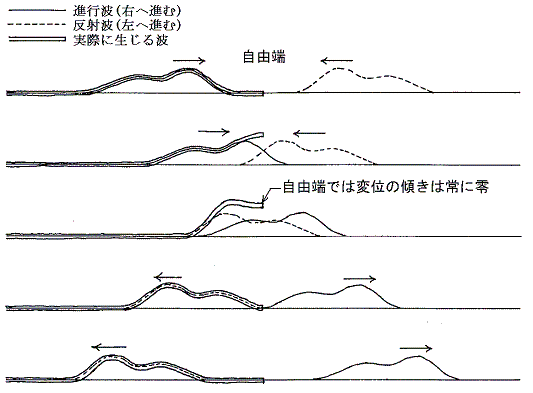
�@���U���N���邽�߂ɂ͔��˕ǂň͂܂ꂽ�̈�֘A���I�ɔg�����荞�܂�˂Ȃ�Ȃ��B�����āA���̂Ƃ����[�ł̔g�̔��˂��{���I�Ȗ�����������B�����ōŏ��ɍ��Z�����ŏK���g�̔��˂K����B
�@���R�[�ł͏㉺�����̗͓͂����Ȃ��B���̂��߁A�������̎��R�[�ɉ������̗͂���������A���͂��傤�lj�����ꂽ�����̗͂�ł������l�ɓ����B�����ė͕͂K����ɂȂ�A���˒[�͐����̂܂܂ł���B���̂悤�ɂȂ邽�߂ɂ͓��˔g�ɏd�ˍ��킳�锽�˔g�͓��˔g�̏㉺�͂��̂܂܂ŁA���E���Ђ�����Ԃ������̂����˂��ꂽ�ƍl���Ȃ���Ȃ�Ȃ��B

�@
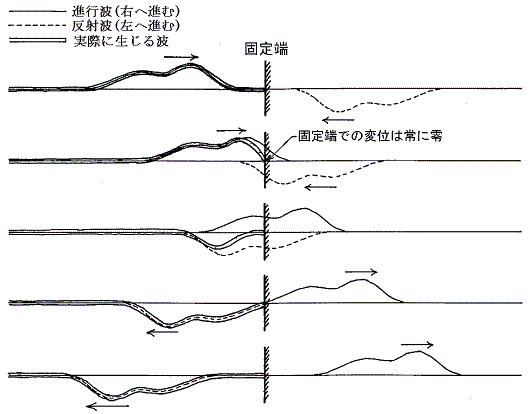
�@�Œ�[�ł͏�����̕ψʂ͗��ł���B���̂��߂ɂ́A���˔g�͓��˔g�̍��E���Ђ�����Ԃ��āA�㉺���Ђ�����Ԃ������̂ƍl���Ȃ���Ȃ�Ȃ��B���̂悤�Ȕ��˔g�����˔g�Əd�ˍ��킳���ď��߂ČŒ�[�ł̕ψʗ낪�����ł���B
�@
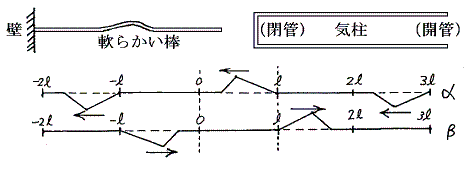
�@���[�����˕ǂň͂܂ꂽ�ꍇ�̔��˂̗l�q��m��ɂ́A���}�̗l�ȓ��˔g�Ɣ��˔g������ďd�ˍ��킹��悢�B�ȉ���Max Planck���u���_�����w�Ę_�@��Q���@�ό`���镨�̗̂͊w�v�R�V�߂̐����𗘗p����B
�@���[�ŌJ��Ԃ����˂���g�̗l�q��\�����߂ɂ͔g�`���Q���@�̒P�ʂō��E�ɃR�s�[���J��Ԃ����g�����������ɁA�܂����Ƃ͂����O�̌��_�ɑ��ē_�Ώ�(���E�ɂЂ�����Ԃ��āA����ɏ㉺�ɂЂ�����Ԃ�)�̔g�����E�����֔g�̓`�d���x�ňړ������āA���ꂿ���킹�悢�B�����ĂO���������̊Ԃɂ��ďd�ˍ��킹��A���ꂪ���߂���ł���B
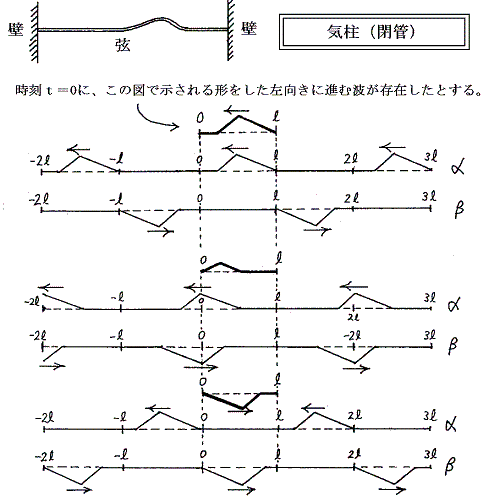
�@���̏ꍇ�͗��[�����R�[���˂ɂȂ�̂ŁA�g���͔g���������O�ō��E�ɂЂ�����Ԃ����`�ɂ���悢�B�g���������ցA�g�����E�����ֈړ������āA�O���������̊Ԃɂ��ďd�ˍ��킹��悢�B
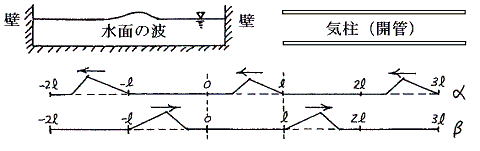
�@���̏ꍇ�͌Œ�[�Ǝ��R�[�Ȃ̂ŁA�g�������Ƃ��A�����Q���@�̒P�ʂō��E�ɃR�s�[���J��Ԃ��Ƃ��A�㉺���Ђ�����Ԃ��Ȃ���R�s�[����悢�B�����Ĕg���͂����O�̌��_�œ_�Ώ̂ɂȂ�悤�Ȍ`�ɂ���悢�B�g�����������ցA�g�����E�����ֈړ������āA�O���������̊Ԃɂ��ďd�ˍ��킹����ꂪ���߂���ł���B
�@
�@�g�͂ق��Ă����ƁA�ǂ�ǂ�`�d���ē����Ă��܂��B�����狤�U���N���邽�߂ɂ́A�������g���͂��Ă����˂�Ȃ炢�B����ɂ����[���g�˂��������������Ȃ���Ȃ�Ȃ��B����Ɠ����ɁA���U���N���邽�߂ɂ́A�g��A���I�ɋ�������@�\���K�v�ł���B
�@�g���A���I�ɋ��������ꍇ�A�d�ˍ��킹��g���ǂ̗l�ɍ������悢���낤���B�O�߁i�C�j�Œ�[�|�Œ�[�@�̏ꍇ���Ɏ���Đ�������B�O�߁i�C�j�̏ꍇ�ƈقȂ��āA����ǂ͎����Q���œ]�ʂ��ׂ��g�̒��������ԂƋ��ɂ�����ł������Ȃ�B���������ׂďd�ˍ��킹�����i�s����g���ƁA�������E�ɐi�ޓ]�ʔg�����ׂďd�ˍ��킹���g�����O�`���̋�Ԃŏd�ˍ��킹�����̂���ԂO�`���Ŏ��ۂɐ�����g�ł���B
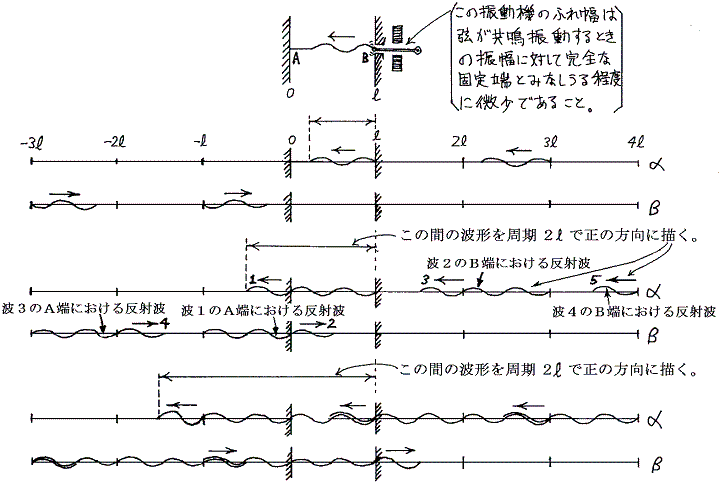
�@���ƃ��̔g���d�ˍ��킹�Č���Ή��邱�Ƃł��邪�A�}���̒����@���@���g���ɂ̔������{(���g���̐����{�̂���)�̏ꍇ�݂̂��ׂĂ̔��˔g�݂͌��ɋ��ߍ����}�����傫���U������B��������U�i����)�����Ƃ����B����ȊO�̏ꍇ�݂͌��ɑł����������Ă��܂��A�U���͏����Ă��܂��B
�@
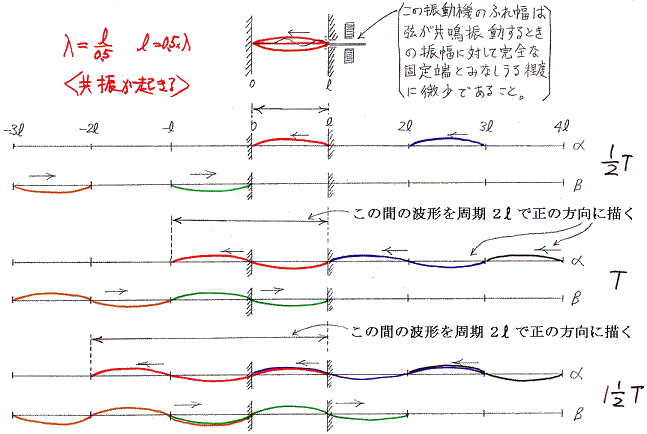
���̗�ł͑��荞�܂ꂽ�g�����˂��J��Ԃ����ɂ��݂��őł����������Ă��܂��ċ��U�͋N����Ȃ��B
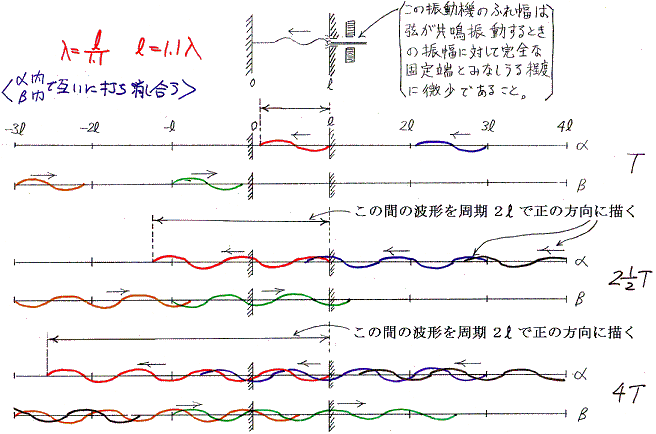
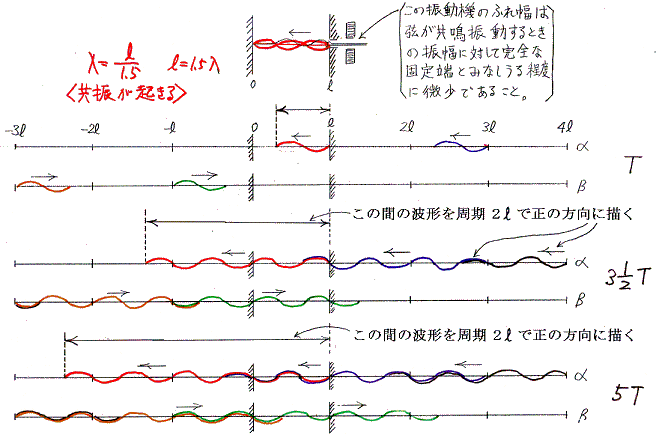
���̗�ł����U�͋N����Ȃ��B
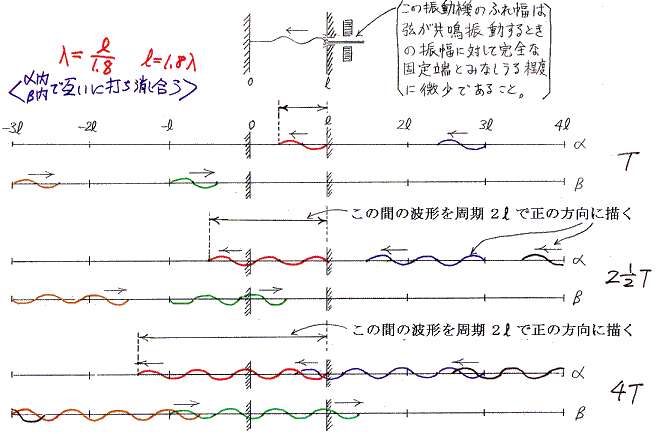
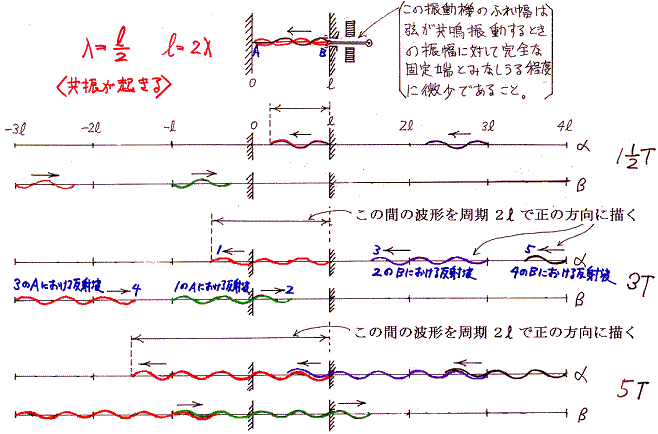
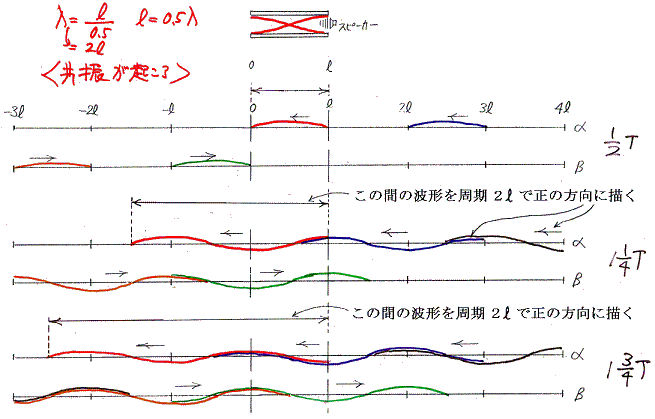
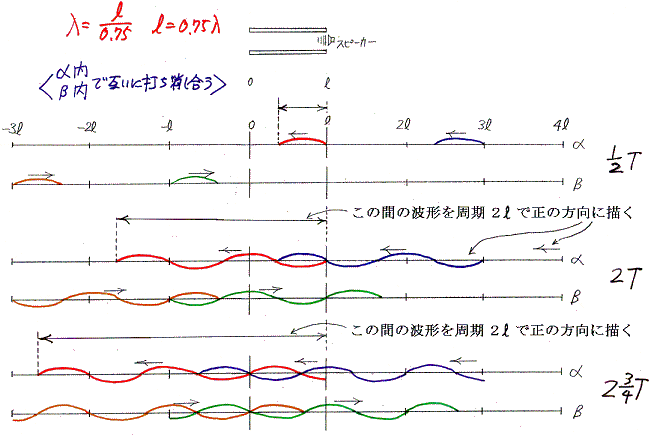
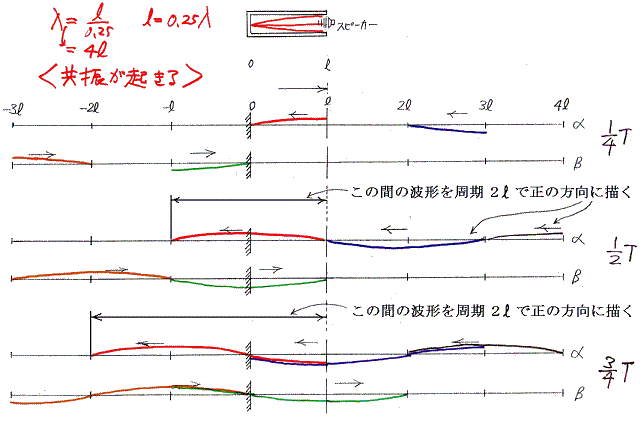

�@���˒[�ň͂܂ꂽ�����@���@�̔}�����ɑ��荞�܂��i�s�g�̔g�����@�Ɂ@�Ƃ���ƁA�O���Q�D�i�P�j�i�Q�j����������Ή���悤�ɁA���ƃɂ��ȉ��̊W�����Ƃ��̂��U���������Ē��g�������}���͑傫���U������B
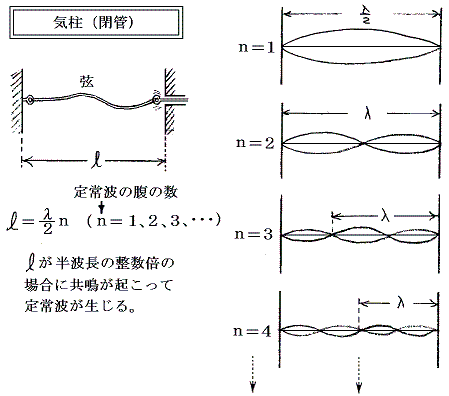
�@
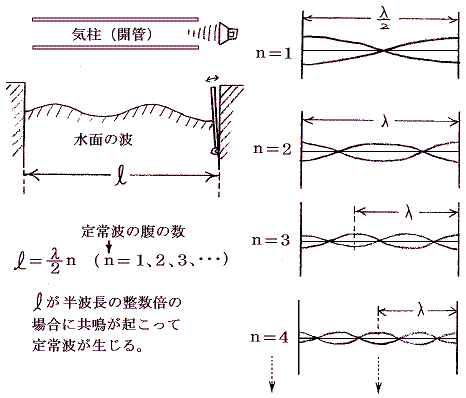
�@
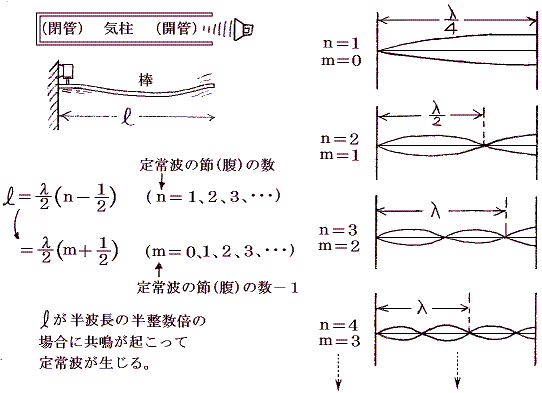
�@�����̌������o����ɂ́A�܂��Œ�[�͐߁A���R�[�͕��ɂȂ���g�̌`��}�Ŋo����B���Ɂi�C�j�i���j�̏ꍇ�A�}���̒����@���@���m�i�s�g�̔��g���n�́m�����{�n�ŋ��U���A�i�n�j�̏ꍇ�A�����@���@���m�i�s�g�̔��g���n�́m�������{�n�ŋ��U���鎖��}����ǂݎ��B���ꂳ������A��́@�����Ɂ^�s�������@�̊W����p���ā@���@�Ɓ@���A���A�s�@�Ƃ̊W�������Ƃ��ł���B
�@
�i�s�g�̔g�����ɁA�`�d���x�����A�U���������s�A�U���������Ƃ����
![]()
�̊W�������藧�B����͍��Z�����ŏK���g�g�ōł��d�v�ȊW���h�ł��B
�@���̎��̒����g�̓`�d���x�@���@�͔}���̏E�����ɂ�茈�܂��B�Ⴆ��
�����̌����̓��o�͕ʍe�u�g���������ƈ�ʉ��v2�D���Q�Ƃ��ꂽ���B
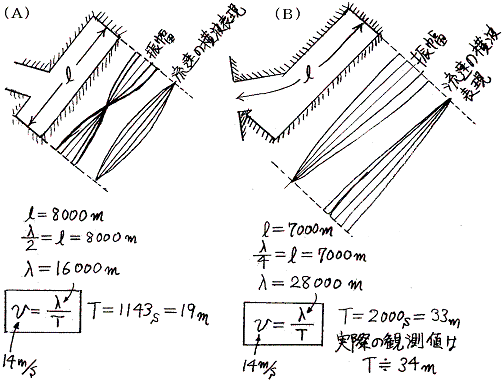
�@�`�d���x���������I�ɂ�茈�܂�A�R�D�i�C�j�i���j�i�n�j�����U�����������g�����̔g�𑗂�o���U���@�\���U�������s�́A�s���Ɂ^���@���狁�܂�B
�@
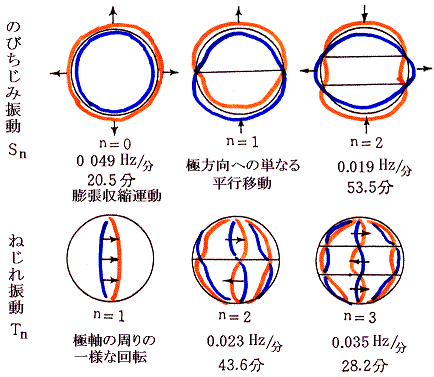
�@���܂����ג����p�͒��g�̐N���ɔ����A���̌ŗL�U�����ŐU������B���ɒ���p�͗L���ŁA����n���̕����Łu���т��v�Ƃ����B���g�Ƃ͔g���ɂ����[�����ꡂ��ɒ����g�̂����ŕʍe�u�g���������ƈ�ʉ��v�Q�D�i�S�j���g�@�Ő����B���̓`�d���x��
![]()
�ŕ\�����B����p�̕��ϐ��[�͖�Q�O���ł��邩�礒��g�́@����(�X�D�W�~�Q�O)1/2���P�S���^���@���x�Řp����i�s����B�V���L���Ⓑ��C�m�C�ۑ�̕��ɂ��Ƌ��U�̐U�������͖�R�S�����x�ł���B����p�̌`�͈ȉ��̖͎��}�̂悤�Ȃ��̂ŋߎ��ł���B�i�`�j�^�C�v�̋��U�Ɓi�a�j�^�C�v�̋��U�i�p�����߂Řp�������j���l������B���U�������炻�ꂼ�����{�U���̎��������߂Ă݂�B�i�`�j�^�C�v�͖�P�X���A�i�a�j�^�C�v�͖�R�R���ɂȂ�̂ŁA�����炭�u���т��v�́i�a�j�^�C�v�̐U������ɂȂ�Ǝv����B
�@
�@�J�i�_�̃m���@�E�X�R�V�A�ɂ���t�@���f�B�p�ł͒��ʍ������E�ōł��傫���B���ɑ傫�����ʍ��𗘗p���āA�����̂Ƃ��ɑ傫�ȖԂ𗧂āA�����̊Ԃɂ������������A���̊����̂Ƃ��ɏE���W�߂鋙�@�����邭�炢�ł��B
�@�p�̓����ł̒��ʍ��͂��܂�傫���Ȃ��A�咪�̂Ƃ��ł��R�������Ȃ����A�p���̃Z���g�W�����ł͒��ʍ��͂V�`�W���ɂȂ�A�ł����̃W�O�l�X�g�̓��]�ł͂P�S���ɁA�܂��}�C�i�X���]�ł͍ł��傫���A�P�T���ɂ��B����B��������ƒ��ʍ��͂���ɂQ���قǑ傫���Ȃ�B
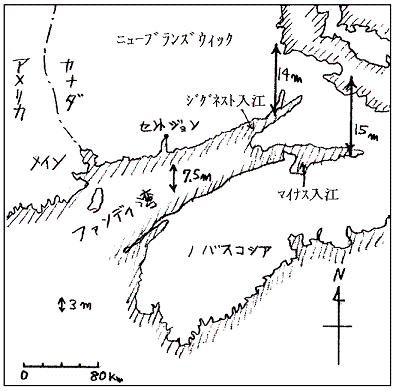
�@�t�@���f�B�p�̕��ϐ��[�͖�T�O���ł���B���s�����Q�T�O�����ƌ��Ȃ�����{�U���̎��������߂Ă݂�B�����g�́i�P�j����p�́u���т��v�̏ꍇ�Ɠ��l�����g�Ƃ݂Ȃ���̂ŁA���̓`�d���x���́@
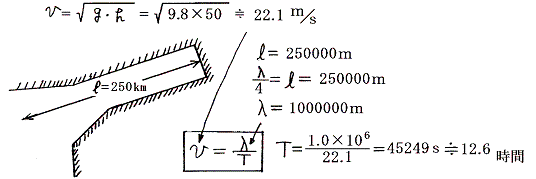
�@���Ȃ肨�������ςȌv�Z�œ����s���P�Q�D�U���Ԃ����A�����̎����P�Q�D�S�Q�����ɋ߂��B���̂��߂ɋ��U���N����傫�Ȓ��ʍ�����̂ł��낤�B�����̐����郁�J�j�Y���ɂ��Ă��u�����͂ɂ��āv���Q�ƁB
�@
�@�I�����_���{�̓]�C�f���C�̎��ӂ̊����i�߂�ɓ������āA����n��k�C����P���Ă��鍂�������邽�߂ɁA�]�C�f���C�̓������R�O�����̒���ȃ_���łӂ�������v��𗧂Ă��B�������]�C�f���C�̓������ӂ����ƃ��b�f�������ƃ_���̊Ԃɂ͂��܂ꂽ�����̒������傫���Ȃ�A���b�f���C���݂̒�h�͍X�ɍ������̂ɂ��Ȃ���Ȃ�Ȃ��B������ǂꂭ�炢�Ɍ��ς���ׂ����ꗶ�����B
�@�����ŃI�����_���{�͍����ȕ����w�ҁ@H.A.Lorentz�@���ψ����Ƃ���ψ�����P�X�P�W�N�ɍ��A���̒����������s�����ɂȂ����B�W�N�Ԃɂ킽�钲���ƌ������d�˂����ʓ���ꂽ���̂́A�]�C�f���C���d��ƃ��b�f���C�̊����̐U������Q�{�ɂȂ�A���b�f�������̓��X�̓����Ԃ̗��ʂ��_������邱�Ƃɂ���Ă������đ����Ƃ����ӊO�Ȃ��̂ł������B����͂��傤���k�C���痬�ꍞ�ޒ����̔g�ƁA�_���ɂ���Ĕ��˂��ꂽ�g�������Ē��g��������A���傤�ǃ��b�f�������̏��ŁA���̐U���͋ɏ��ƂȂ�A���ʂ��ɑ�ɂȂ����Ƃ��Ӗ����Ă����B
�@�I�����_���{�́A���̕��ĂP�X�Q�V�N�`�P�X�R�Q�N�A���ɂ��̑�H���������������B����͐����A�Ȋw�A�Z�p�̍ł����������̗͂�ł���A�܂������قǂ݂��Ƃɐ���������ł���B���̊Ԃ̎���ɂ��Ă�
�@���i�U��Y���@�u�]�C�f���C�̐��h�ƃ��[�����c�v�@�������_�Ђ̎G���u���R�v�i�P�X�U�O�N�P�����j
�ɏڂ����Љ��Ă���B�̓ǂ�Ŋ����[�������̂ŁA�����ɑS�������p����B
�@
�@��ؖ����̎�s�\�E���̌��֍`�C���`�����i�m��j�̑咪�����L���ŁA�咪�̎��ɂ͂P�O�����z����B�����͒��N�푈�̋A�����������m��㗤����̕���ƂȂ����ꏊ�ł���B
�@���N�푈�͂P�X�T�O�N�U���Q�T�������A���N�l���R�̖k��38�x�����z����N�U���Ŏn�܂����B�ŏ��̂V�O���Ԃ͒��N�l���R�̈��|�I�D���̂����ɐi�W���A�N�U���Q�W���̊؍��̎�s�\�E���ח���A���A�E�؍��R�͂X�����߂ɂ͑��(�e�O)�A���R(�v�T��)���܂ޔ�����[�̋�����p�ɒǂ��l�߂�ꂽ�B�����ō��A�R���i�ߊ��̃}�b�J�[�T�[�͒��N�l���R�̔w���˂��A�N���̐m��i���C���`�����j�㗤�����P�X�T�O�N�X���P�T���Ɋ��s�����B
�m�g����n
�@�m���͏㗤���ɂނ��Ȃ��n�`�ł���B���̊����Ŋ������ɂ͊C�݂��琔�L�����̓D�y�n�т����܂�㗤�ł��Ȃ��B�㗤�ł���̂͑咪�̐����ԁA�������P���Q��̖������̂Q�`�R���Ԃ̊Ԃ������B�܂��C�ݐ��ɕl�ӂ��Ȃ��A�h�g�炩�V���Ƀn�V�S�œo�邵�����@���Ȃ������B���̏㗤�̍���䂦�Ɉӕ\������킾�����B
�@�P�X�T�O�N�X���P�T������������͂R�D�V��(�ג����O����)�ŁA�咪���璆���ֈڍs���̊�����������A���̓��̖����͑����Ɨ[���ł������B��ʂɒ������ۂ͘p�̌`�i�����ł݊͟C�Ɖ��C)�⒪���g�̓`�d���x�i���[�ɊW�j�ɊW����̂ŁA�������������̕����ƈ�v����Ƃ͌���Ȃ��B�ʍe�u���͊w�I�������_�ɂ�����P���r���g�v�T�D�i�Q�j�Q�D������P�T���ɂ������g���������h�̐m��ʉߎ����i�S���ƂP�U�����j����l����ƁA����R�D�V���̏ꍇ�����Ɨ[���ɖ����ƂȂ�̂�����B
�@�X���P�T���ߑO�T���A���A�R�͍ŏ��̏㗤�n�_�ł��錎�����i�m��`�ɗאڂ��鏬��)�Ɋ͖C�ˌ����J�n���A���̓����ŏ��̖����ɏ悶���U���R�P���ɐ攭�������㗤���J�n����B�����̒�R�͎U���I�ŌߑO�V���T�O���ɂ͑|������������B�����Ă��̓����Q��ڂ̖����ɍ��킹���ߌ�T���R�R���Ɏ�͕������㗤���A��R��r�����^�钆�ɂ͐m��̖k���Ɠ암�ŖڕW���ɓ��B����B���P�U���[���ɂ͐m�삩��10�L���̉~��Ɏw�肳�ꂽ�C�݂��m�ۂ����B
�@���̊�P�㗤���̐����ɂ��m��A�\�E����D�҂������A�E�؍��R�͂P�O�����߂ɂR�W�x����˔j���A�����P�X��������́A�ꕔ�̕����͊��](������傭����)�݂܂œ��B�����B�������P�O���Q�T���A�����l���R�̑啔�������]���z���ĎQ�킵�A���N�l���R�ƂƂ��ɔ������A�P�Q���S���ɂ͕����D��A���T�P�N�P���S���\�E�����Đ�̂����B���̌�A���A�E�؍��R�͂R���P�S���\�E�����ĒD�����A�R�W�x���t�߂ł̐퓬�͌�����ɂߑ����̐l�X���펀���A������P����ԂƂȂ�B�����ĂT�R�N�V���Q�V���A�悤�₭��X(�͂����Ă�)�ł̋x�틦�蒲��ƂȂ����B���̋x�틦�肢�炢��k���N���f�̔ߌ��͍����܂ő����Ă���B
�@
�@�����w�r���̊�{�U���̎����́m�����̊K���n�~�O�D�P�b���x�ŁA�Ⴆ�R�U�K���ĉ����փr���́@�s�`�S�b���x�ł���B�r���������Ă����Ղ̌ŗL�U�������i�`�O�D�R�b���x�j�ƁA�r���̌ŗL�U����������v���Ȃ��悤�Ƀr����v���Ȃ���Ȃ�Ȃ��B
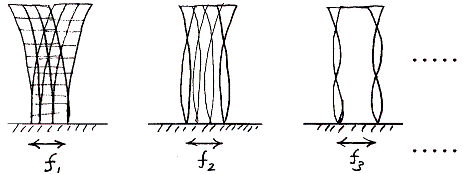
�@�����̉����̒n�Ղ͓�炩���ŗL�U�������͂O�D�V�`�P�b���x�A�R�̎�̒n�Ղ͌ł��O�D�R�b���x�ł���B�֓���k�Ёi�P�X�Q�R�N�j�̂Ƃ������ł͖ؑ���K���ĉƉ��i�ŗL�U���������O�D�V�`�P�b���x�j�̓|�����A�y���̔�Q�͏��Ȃ������B����A�R�̎�ł͓y���i�ŗL�U���������O�D�R�b���x�j�̓|��̔�Q�������ؑ���K���Ă̔�Q�͏��Ȃ������B��������U���������B�i�|���ρu�n�k�̉Ȋw�v���{�����o�ŋ���P224���j
�@
�@�n���\�ʂ���l�ɕ����Ă����C�̒����^������������Ƃ���ł���B���ۂɐԓ��n�тő�C�̋C���ω��𑪒肷��Ɖ��L�̗l�ɂȂ�B
�@���̌��ʂ�����邱�Ƃ́A��C���̐U���͊C�̒����ƈقȂ�A���X�̓V��ω��ɔ����C���ω�(���C�����C���̈ړ�)�����Ȃ�e������B�������A����ɂ�������炸�A24���Ԏ�����12���Ԏ����̌����ȐU�����������Ƃ��ǂݎ���B
�@����ɐ��E�e�n�̓��l�Ȋϑ����r���Ă݂�ƁA�����U���͐ԓ��t�߂ōő�U���������A���ɕt�߂ł͏����Ă��܂��B�܂��U���͌o�x�����ɂ͂قƂ�Ǖω����Ȃ����Ƃ��������B�����Ă���ɏd�v�Ȏ��Ƃ��āA���ׂĂ̒n�_�ŁA�ō��C���͂������n�����̓�������(�ߑO�X���R�O�����ƁA�ߌ�X���R�O����)�ɋN�����Ă��邱�Ƃ��������B(���}�Q��)
�@��������ɕs�v�c�Ȃ����ł���B�ʍe�u�������v��u���������v�Œ��ӂ����悤�ɊC�m�̒������P�Q�D�S�Q����(��P�Q���ԂQ�T��)�����ŋN����B����ɑ�����C�̒����͐��m�ɂQ�S���Ԃ��邢�͂P�Q���Ԏ����ŋN�����悤�Ɍ�����B
�@�P�W�O�O�N�̑������t�����X�̑吔�w�҃��v���X�����łɂ��̂��ƂɋC�t���Ă���A��C�̒����͑�C�̑��z���˂ɂ����M���傫�Ȍ����ł���A���z�⌎�̈��͂ɂ���ċN������̂ł͂Ȃ��ƌ��_���Ă���B
�@�Ƃ��낪�A���������Ȃ������V���ȋ^�₪�������B���z���˂������Ȃ�P�Q���Ԏ��������Q�S���Ԏ�������z����͂��ł���B�������ϑ����ʂ͂Q�S���Ԏ��������P�Q���Ԏ����̕������炩�ɑ�z���Ă���B����͑傢�Ȃ�^��ł��������P���r�����͂��̗��R�����̂悤�ɐ��������B
�@�u�C���̔��������ω��̌����́A���z�̏d�͂ɂ�钪���������ʂł͂��蓾�Ȃ��B�Ȃ����Ƃ����ƁA�����d�͂ɂ��Ƃ���Ȃ�ρA�����Ƒ傫�Ȍ��̉e�����łȂ���Ȃ�Ȃ��̂ɁA���ۂ͑��A���C���ω��͑S�R�����Ă��Ȃ����A���邢�͂قƂ�nj����Ă��Ȃ��B������A�C���̔��������ω������x�ɂ�邱�Ƃ͊m���̂悤�Ɍ�����B�Ƃ��낪�A�C���̓��ω��̒��a��͂ɂ������������̍��́A�^�����Ȃ����ׂĂ̒n�_�A���邢�͂قƂ�ǂ��ׂĂ̒n�_�ŁA���������̍������͂邩�ɑ傫���B�Ƃ��낪���x�ω��̋C�����ʂ̔��������̍��̉e�����A��������̂��̂��͂邩�ɑ傫���Ƃ������Ƃ́A���Ɍ����Ȃ��Ƃł���B�v�E�E�E�E�E�E�E�E�E�E�E�E�E(�傢�Ȃ閵��)�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�u���̂��Ƃ̐����́A��C�S�̂Ƃ��Ă̐U�����A���v���X�̂��̌������g���čl���邱�Ƃɂ���āA�������t���邱�Ƃ��ł���ł��낤�B���̃��v���X�̌����Ƃ����̂́A�ނ̒����w�V�̗͊w�x�̒��ŁA�C�̒����ɑ��ė^���A���ꂪ��C�̏ꍇ�ɂ��K�p�ł��邾�낤�ƌ��������̂ł���B�N���͂Ƃ��ďd�͂ɂ��͂̂����ɔM�̉e���ő�p���A�܂��M�I�e���̈�������A���������̍��̂��ꂼ��ɑ���U���̗l���ׂ�A�������̗l�Ȃ��Ƃ����o�����ł��낤�B���Ȃ킿��C�̎��R�R�U���̎����́A���������̕��ɋ߂��̂ł���A�܂����ꂾ����A���������̕����A�N���͂������������ɂ�������炸�A���ꂪ���Ƃł����钪�����傫���̂ł���B�v(�G�W�\�p���̉�������̉�����P�W�W�Q�N)
Lord Kelvin(W. Thomson), �gOn the thermodynamic acceleration of the earht's rotation�h, Proc. Roy. Soc. Edinb., Vol.11, p396�`405, 1882�N ����̓l�b�g����_�E�����[�h�ł��܂��B�܂��ނ̘_���W�V��p341�`350�ɂ�����B
�@�܂�A��C���g���U���̌ŗL�����������Ă���A���̎����͂P�Q���Ԃɋ߂����ɂ���Q�S���Ԃ���͊O��Ă����B���̂��߂Q�S���Ԏ����̑��z���M�ɂ�鋭���U�����P�Q���Ԏ����̐U�������Ă���ƌ����킯�ł���B
�@�������Ȃ���A�ŋ߂̒m���ɂ��ƁA�P���r���̗\�z�͊Ԉ���Ă����悤�ł��B���w��C�܂Ŋ܂߂��ߔN�̐��m�ȑ�C���x���z�̊ϑ�����A�ŗL�U�����Q�S���Ԏ��������P�Q���Ԏ����ɋ߂����Ƃ����������͖������Ƃ����������B�ǂ����P���r���������悤�ȒP���Șb�ł͖����悤�ł��B
�@�A�c�E���u�n�����߂��镗�v�����V���i1983�N���j��X�͂ɁA1966�N�ɂ��̓���𖾂��������i����c�F���̎d�����ȒP�ɏЉ��Ă��܂��B���̐����ɂ��ƂP�Q���Ԏ�������z����̂���C�d�͔g�̐��������`�d�̐U�����ˑ����ɂ���悤�ł��B���z���˂����w���I�]�������M�����Ƃ��A�������̂ق��͑�C�𐂒��ɓ`��邱�Ƃ��ł��āA��C�̉��M����C�S�w�ɓ`���A�n��̋C���v�ł͂�����Ɗϑ������B����ɑ��Ĉ�����̂ق��͐����ɓ`���Ȃ��g���̂��߂ɉ��M���I�]���w�ɂƂǂ܂��C�S�̂̏d���Ƃ��Č����n��C���͂���قǕϓ����Ȃ������̂ł���B
�@���̉���L�����Q�Ƃ��ꂽ���B
��c���g���A�g�G�l���M�[�̔g���B�d�ɂ������C�\���̖����h�A�u�V�C�v1955�N4����
http://www.metsoc.jp/tenki/pdf/1955/1955_04_0090.pdf
��c���g���A�g�C���̔��������̌���闝�R�h�A�u�V�C�v1975�N6����
http://www.metsoc.jp/tenki/pdf/1975/1975_06_0315.pdf
��c���g���A�u�����w��Ԃ̓�v�u�k�Ѓu���[�o�b�N�X�i1979�N���j��13�͎Q�ƁB����ȊO���ʔ����{�ł��B
�@�P�W�W�R�N�ɃN���J�g�A�ΎR�i�C���h�l�V�A)���唚�����ē��̔�������������ꂽ�B��C���ł��̂������������N�������̂ŁA��C�̌ŗL�U���̎����𑪒肷�邱�Ƃ��ł����B�l�X�ȐU�������̂Ȃ��ŁA�P�Q���Ԃɍł��߂��ŗL�U���̎����͂P�O�D�T���Ԃł������B�i�������A����̓g���|�|�[�Y�̔��˓����Ɉ��邽�߂�������Ȃ��B�j
�@���̂P�Q���Ԏ����̋C���ϓ������������͂��ł���B�n�\�t�߂ł͂���͋ɒ[�ɏ������قƂ�NJϑ��Ɋ|����Ȃ���������Ȃ����A���w��C�ł͂��̕ω��͔��ɑ傫�Ȃ��̂łȂ���Ȃ�Ȃ��ƍl�����Ă����B�P�X�T�O�N��ɂȂ��đ�C���w�̕����������ł���悤�ɂȂ��āA���̂��Ƃ��^���ł��邱�Ƃ��m���߂�ꂽ�B���x100�����t�߂̒������͕������\���^���ɒB���A�U���Ԃ��Ƃɕ��������t�]���Ă����̂ł���B(���}�Q��)
�@���̊ϑ����ʂ́A�����̔������[�_�[�ŒǐՂ���u�d�g�����@�v�ƌĂ����@�œ���ꂽ���̂ł���B�����������́A�������ɂ������w��C�ɍ~�蒍���ł���B���̒��̂����傫�����̂��u�����v�Ƃ��Đl��̖ڂŌ��邱�Ƃ��ł���B�������ڂɌ����Ȃ��������A�ʂ�H�̋�C��d�����ăC�I���̒�(��)���c���B�������c�������̒��̎��R�d�q�ƃC�I���́A���g���R�O���K�w���c�t�߂̓d�g�M����ǂ����˂���B�����̔��ːM���̈ړ����x�̑��肩��A���w�œd�����������̔��𐁂������Ă��镗�̕����Ƒ��x��m�邱�Ƃ��ł���B����͒n�ォ��A������������킸�A���I�ɍs�Ȃ���̂Ŕ��ɕ֗��ȕ��@�ł���B�������A�W�O�����ȉ��ł͏\���Ȑ��̗����̔����Ȃ����A�P�O�T�����ȏ�ł́A�����̔������܂�ɑ��������Ă��܂��̂ő���ɂ�����Ȃ��B���̂��߂��̕��@�ő���ł���̂́A���x��W�O�`�P�O�T�����̊Ԃ̕������ł���B
�@�C���O�����h�̃W��h�����E�o���N�ƁA�I�[�X�g�����A�̃A�f���[�h�ɂ���d�g�{�݂ɂ�钷���Ԃ̑��茋�ʂƁA��ɑ嗤�̃��[�\���̓�A�O�̑���Ƃ��A��C�����̌����Ɏg��ꂽ�B�������p�ɂɌ�����悤�ȓ��ɂ́A�Q�O�����Ƃɕ��ϕ��̑��肪�s�Ȃ�ꂽ�B��}�́A�W���h�����E�o���N�̏��W�O�`�P�O�T�����Ԃ́A�P�X�T�S�N�X���P�U�����߂���P�V�����߂܂ł̕��̕ω��̗l�q�ł���B�}�ɂ͓삩��k�������̐����������Ă���A�e�_�͂��̕����̈ꎞ�Ԃ�����̕��ϕ����ł���B�ߌ�S�����ɂ͕��͖k�������ĂQ�O���^���̑����Ő����Ă��邪�A�U���Ԍo�����ߌ�P�O�����ɂ́A�قƂ�Ǔ��������œ�������Đ����Ă���B�����Ă���ɂU���Ԍo�����ߑO�S�����ɂ́A�Ăіk�������Đ����Ă���B�����ׂ����ɁA�P�Q���Ԏ����ł̕����ω��͂S�O���^���ɒB����B(���`���[�h�E�`�E�N���[�O���@����̉Ȋw26�u�F����Ԃ̉Ȋw�v�͏o���[�V�Ё@���)
�@
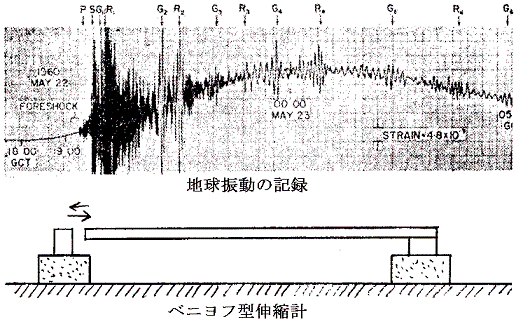
�P�X�U�O�N�T���Q�Q���ɋN�������`���n�k�i���[�����g�}�O�j�`���[�h9.5�̊ϑ��j��ő�̒n�k�j�̋L�^�i�J���t�H���j�A�H�ȑ�w�@�x�j���t�^�L�k�v�ɂ��j�i�|���ρu�n�k�̉Ȋw�v���{�����o�ŋ���P50���j
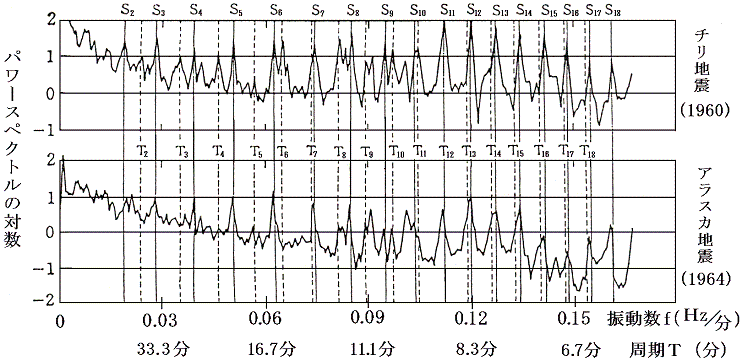
��L�n�k�L�^���狁�߂��A�e�U�������̐U�����ǂꂭ�炢�̋��x�Ŋ܂܂�Ă��邩��\���}�B
�@
�@NPO�@�l�Ȋw�f���ق����J���Ă���f��t�B�����u�U���̐��E�v�ɍH�w�ɉ����鋻���[���Ⴊ��������Ă��܂��̂ł����������B���̒��ɁA�݂苴�̃^�R�}������̋L�^�f��������܂��B
�@