剛体の静力学

　ここの内容の大半は、参考文献１．に依存しています。また、文章中でベクトルを記述する必要が生じたら、太字のアルファベット文字でもって表すことにします。

１．剛体に働く力

（１）剛体

　物理学に於いて実際に取り扱う物は、単なる質点ではなくて、有限の広がりを持つ物体です。そのとき、物体は非常に多くの質点が集まって構成されると考えることができるので、物体の運動の法則も質点系の力学に帰する。その見解に立てば、自然界には質点相互の間に生じるもの以外の力は存在しない。つまり各質点は宇宙にある他の全ての質点から受ける合成力に依って運動する。
　ある物体の全体が他に一つの力をおよぼすとか、また他から力を受けると言い方は、説明を簡単にするための方便にすぎない。実際、物体の各質点のみが力の源であり、一方では着力点となる。つまり定まった質点Ａが他の定まった質点Ｂに作用する。その時、自然界にある全ての力は対を無し“作用反作用の原理”を満たしている。

　質点系の各点の相互距離が一定であるものを“剛体”と名付ける。剛体は、その全ての部分に於いて不変の形を保っており、任意の力により全体として運動することができる。この稿の目的は剛体について以下の問に答えることです。

　静止している任意の大きさの剛体の中の様々な“着力点”（高校物理では“作用点”と言うが、この稿ではこの言葉はモーメントの働く点に用いる）に定まった大きさと方向を持つ多くの力が作用すると仮定する。
　このときに、これらの力が平衡を保つ（つまり剛体が静止し続ける）為の条件は何か？また、平衡が満たされていないときに、平衡を保つためにはいかなる力を付加する必要があるか？
　正確には、“平衡を保つ”と言う言葉の中には、等速度運動を続ける場合や、一定の角速度で回転を続ける場合も含ませるべきです。しかし、ここでは簡単に静止し続けることとしておきます。

（２）力の着力点

　これらの問いに答えるために、与えられた力をできるだけ簡単な形になおし、特別な場合から一般の場合に進んでいく。最も簡単な場合は、ただ二つの力が作用するときです。二力が一つの剛体に作用して平衡を保つためには、その二力の大きさは等しく方向が反対であることが必要です。さらに着力点Ａ、Ｂを結ぶ直線が力の方向と一致していることが必要です。例えば下図の二力の作用点がＡとＢではなくて、ＡとＢ’ならば剛体は回転してしまいます。

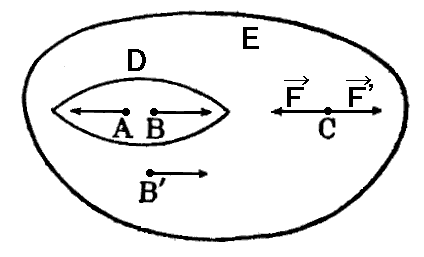
ＡＢの方向が二力の作用する方向に一致していれば、ＡＢの間隔や剛体の形によらず平衡は維持される。このことは、直線ＡＢの垂直二等分面に対して対照的な剛体Ｄに対しては明らかであり、この剛体に全然力の働かない任意の物体Ｅを加えて大きくしてもその平衡が乱されないことから明らかです。
　上に述べた法則から、剛体に作用する力の着力点をその方向に任意の距離移動しても物理的意味に変化を起こさないことが解る。たとえば、物体内で直線ＡＢの延長線上の一点Ｃに二つの大きさ等しく、方向が反対の力ＦとＦ’を置く。このとき、Ｃに於いて右の方に作用する力Ｆ’とＡに於いてその左の方に作用する力は互いに平衡しているから、この二力は同時に取り除ける。そうするとＡに於いて左の方に作用している力の代わりにＣにおいで左の方に作用する力Ｆに置き換えることができる。
　このとき、力Ｆの着力点Ｃは必ず線分ＡＢの延長線上に無ければならないのだから、“力を完全に言い表すためには、その“大きさ”、“作用線の方向”と共に“着力点”が与えられなければならない”ことが解る。
　その着力点の移動は物体内のみならず、その点が物体と固く連結されている条件さえ満たせば、物体外に及んでも差し支えない。

２．力の合成

（１）力が平行でなく、しかも作用線が１点で交わる力の合力

１．平行でない二力の合成

　最初に最も簡単な二力の場合を考える。剛体に作用する二力が、平行でなく、しかも同一平面上にあって、その作用線が１点で交わるとする。この場合は下図の様に、それぞれの力を作用線の交点に於ける力に置き換えて、“力の平行四辺形合成法則”により合成すればよい。

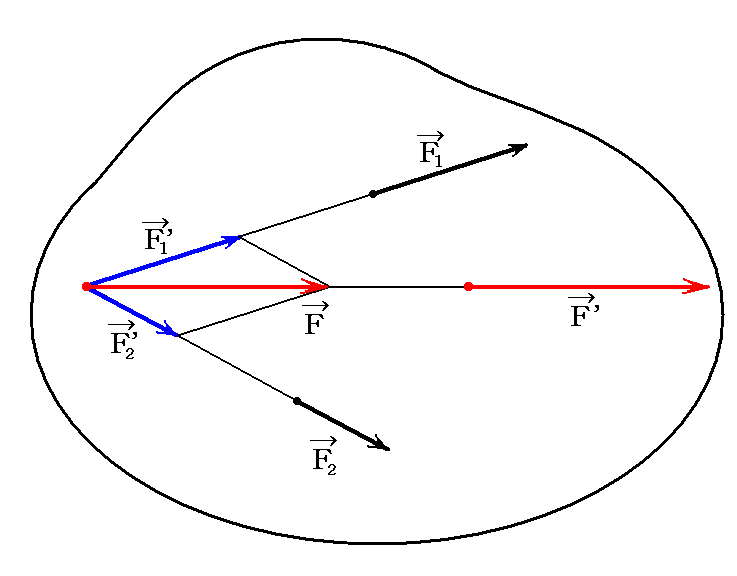
そのとき、合力Ｆはその作用線上を移動させてＦ’としても良い。力が三つ以上ある場合には、まず二つの合力を求め、それに第三、第四、・・・の力を順番に加えてゆけばよい。

［補足説明］
　ここで二つの力が平行ではないが、さりとてその作用線が一点で交わることがない（つまり作用線が三次元空間内で同一平面上になくて、すれ違っている）場合については、ここでは説明しない。もう少し準備をした後に第４章で説明します。

２．１点で交わる多数の力が働く場合

　この重要な例が、別稿「万有引力の法則への補足」で説明した質点Ｐが万有引力の法則に従って剛体物体に引力をおよぼす現象です。

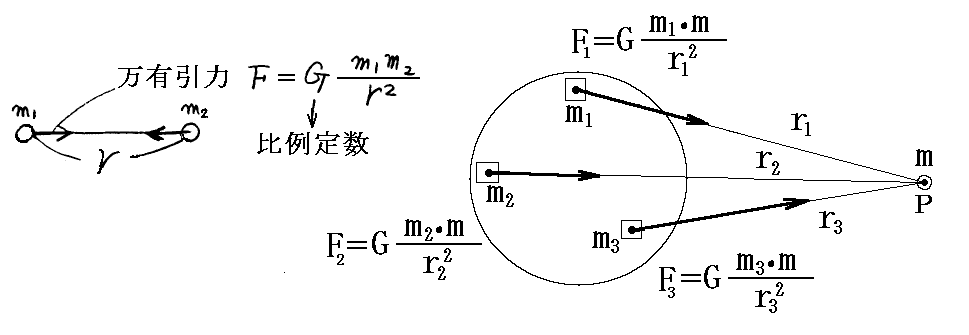
　その引力は一点Ｐが、物体の全ての質量の微小部分に作用するそれぞれの力の合力です。その合力を求めるにはそれらの力を全てＰ点に移動させてそこで合力Ｆにする。そのとき剛体が等密度の球体の場合には、別稿「万有引力の法則への補足」で証明したように、合力Ｆは球の中心と質点Ｐを結ぶ線に沿った力となり、球の中心から質点Ｐに向かう力になる。その合力の作用点を球の中心に移動させれば、あたかも球の全質量が球の中心に存在すると考えたとき、その質量に働く万有引力と同じになる。
　このとき“物体が作用する力”と、“物体が作用される力”の違いに注意しなければならない。質点Ｐは作用反作用の法則に従って上記の力と大きさ等しく方向が反対の力を物体から受ける。

（２）平行な力の合力

１．二力が平行で同一平面上にある場合

　剛体に作用する平行な二力Ｆ₁とＦ₂の合力を求める。この二力は平行でしかも同一平面上にある。この場合には、下図の様に、それぞれの力に仮想的な二力Ｋと−Ｋを付け加えて考えればよい。Ｋと−Ｋは互いに反対方向を向いた同じ大きさの力なので、互いに打ち消し合って、このような力を付け加えても力学的効果は変わらない。
　ＫとＦ₁、−ＫとＦ₂のそれぞれの合力をＧ₁とＧ₂として、それらを交点Ｃに移動して、前節と同様な方法に従って“力の平行四辺形合成法則”により合成する。

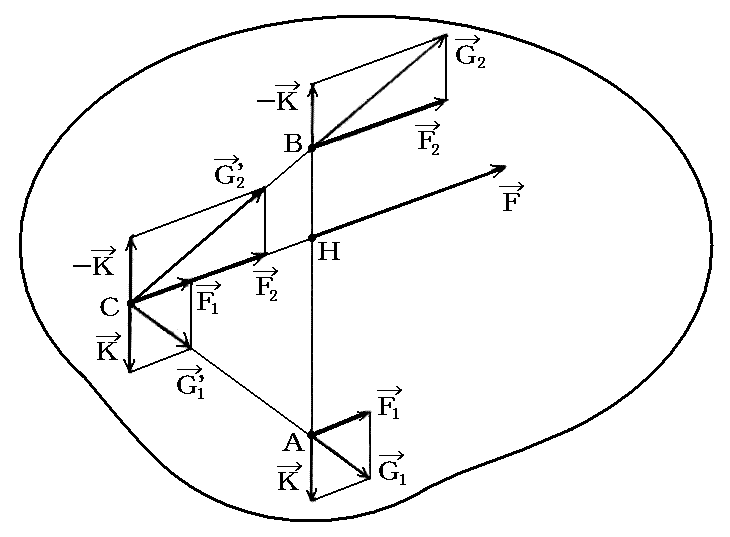
　合成に際して、Ｇ₁’とＧ₂’をもう一度ＫとＦ₁、−ＫとＦ₂に分ければ二つの力Ｋと−Ｋは消えるので、結局合力の大きさはＦ＝Ｆ₁＋Ｆ₂となり、その方向は線分ＣＨの方向を向くことになる。そのとき、合力の着力点は線分ＣＨ上にあればどこに移動しても良いのであるが、普通線分ＡＢとの交点Ｈを着力点に取ると良い。
　この点ＨはＣＨ直線上の他の点とは異なり特別な性質を持っている。すなわち、この点Ｈは二力Ｆ₁とＦ₂との大きさと、その着力点のみによって定まり、二力の方向とは無関係になる。着力点Ｈは、重心の計算などで重要になる。

２．着力点Ｈの性質

　図中の三角形の相似性により、以下の関係式が直ちに導かれる。

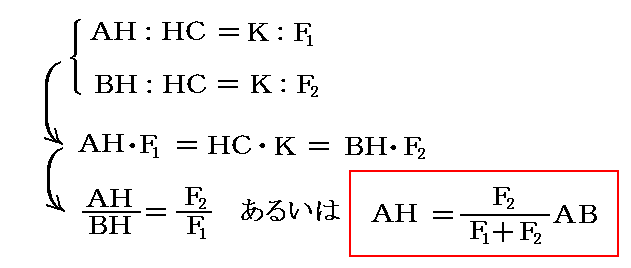
つまり、点Ｈは線分ＡＢを力の大きさに逆比例して内分する点で、必ずＡとＢの間にある。そして、Ｆ₂＝0のときはＨはＡに一致し、Ｆ₂＝Ｆ₁のときにはＨはＡとＢの中点となる。
　そのとき、Ｆ₁とＦ₂との二つの平行力を、大きさを変えることなくＡ及びＢなる着力点のまわりをある角度だけ回転させると、その合力Ｆは、その大きさを変えずに着力点Ｈのまわりを同じ角度だけ回る。

３．着力点Ｈの解析的表現

　平行な力が沢山ある場合を論じるには、着力点Ｈを座標によって表すのが便利です。高校生向きに解りやすくするために二次元座標で説明する。
　力Ｆ₁とＦ₂の着力点であるＡとＢの座標をそれぞれ（ｘ₁，ｙ₁）と（ｘ₂，ｙ₂）とし、合力の着力点Ｈの座標を（ｘ₀，ｙ₀）とすると、下図の様になる。Ｆ₁とＦ₂は互いに平行な関係にある任意の力です。

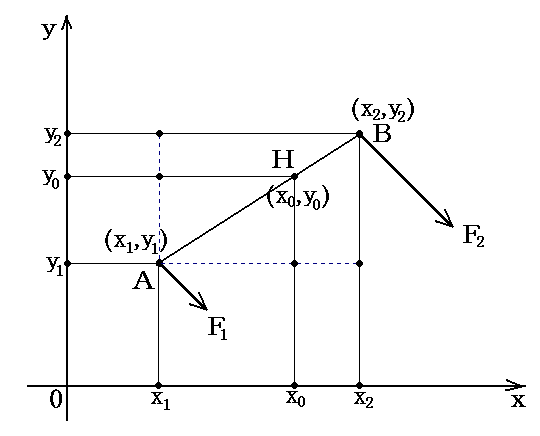
　図中の三角形の相似性に着目すると、直ちに

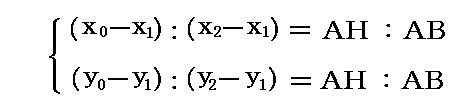
が得られる。ここで、さらにＡＨとＡＢに関する前節の結論を用いると

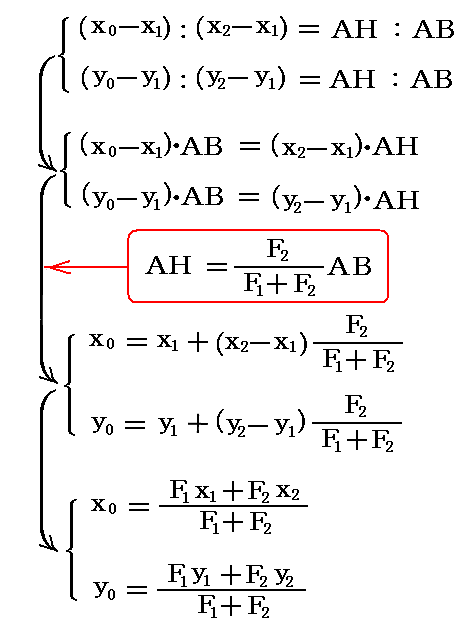
となる。このとき、前節の結論から明らかなように、着力点Ｈに作用する合力Ｆの大きさはＦ₁＋Ｆ₂となる。

　これにさらに三番目の平行力Ｆ₃が存在する場合を考察しよう。Ｆ₃の着力点Ｃの座標を（ｘ₃，ｙ₃）とする。このとき三力Ｆ₁、Ｆ₂、Ｆ₃の合力Ｆ’と、その着力点Ｈ’（ｘ₀’，ｙ₀’）を求めるには、上記表式におけるＦ₁をＦ₁とＦ₂の合力の大きさＦに、Ｆ₂をＦ₃に置き換え、ｘ₁を合力Ｆ＝Ｆ₁＋Ｆ₂の着力点のｘ座標ｘ₀に、ｘ₂をｘ₃に置き換えれば、ＦとＦ₃の二力の合力に対して成り立つ表式となる。つまり、上記の結論がそのまま利用できる。
　すなわち

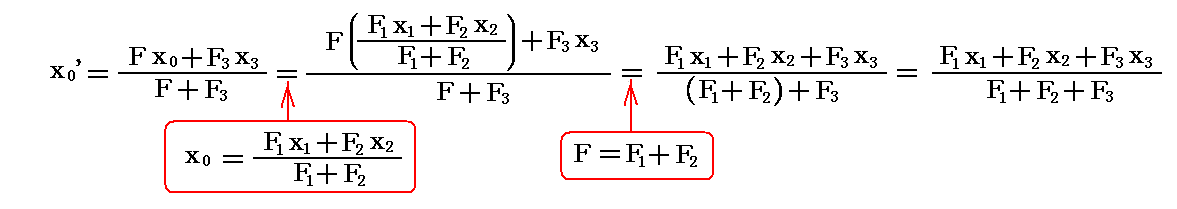
となる。
　ｙ成分についても、全く同様に考えれば

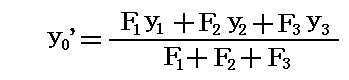
が得られる。このとき、合力の大きさはもちろんＦ’＝Ｆ₁＋Ｆ₂＋Ｆ₃となる。
　平行力が多数ある場合には、上記の手順を順番に繰り返して、次々に加え合わせてゆけば良い。三次元の場合も同様です。

　一般的に、一つの剛体に、互いに平行な多数の力Ｆ₁、Ｆ₂、Ｆ₃、・・・・が着力点（ｘ₁，ｙ₁，ｚ₁）、（ｘ₂，ｙ₂，ｚ₂）、（ｘ₃，ｙ₃，ｚ₃）、・・・・に働いているとき、合力の大きさはＦ＝Ｆ₁＋Ｆ₂＋Ｆ₃＋・・・・となる。
　また、合力Ｆの着力点の座標（ｘ₀，ｙ₀，ｚ₀）は

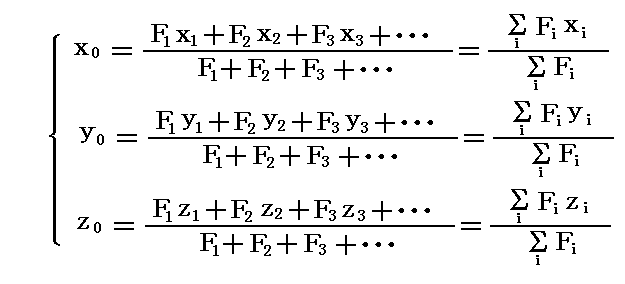
となる。

４．重力への応用

　上記法則の重要な応用が、剛体に地球の重力が働く場合です。剛体に作用する全ての力（重力）の合力Ｆを求める。剛体質量の微小部分ｍ_iに地球がおよぼす力はｍ_iｇで、その方向は地球の中心に向かっている。剛体の大きさは地球の中心からの距離に比較して小さいので、剛体の個々の微小部分ｍ₁、ｍ₂、ｍ₃、・・・に作用する引力は全て平行な力であると見なせる。そのため前項の結論が利用できる。Ｆ_ｉ＝ｍ_iｇを前記の式に適用すれば、剛体に働く重力の大きさは

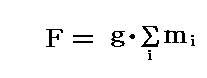
である。
　また、合力の着力点の座標（ｘ₀，ｙ₀，ｚ₀）は、重力加速度が一定なのでΣの外に出せて分母分子で約分でき、

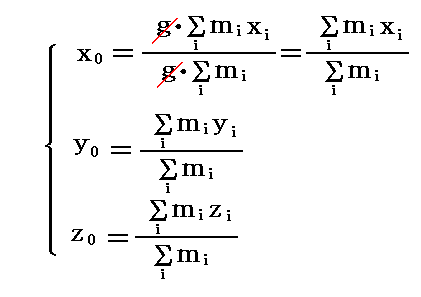
となる。この式によって定められる点（ｘ₀，ｙ₀，ｚ₀）をその剛体の“重心”と言う。
　その位置は、重力の方向及びそれに関わる加速度ｇの大きさには無関係で、ただ剛体内の質量の微小部分の配置のみに因る。そのため、この点は重力の合力の着力点と言うよりも“質量の中心”と言った方が良い。

　質量の微小部分の各部分が固く結ばれていない場合でも、“重心”を定義できる。すなわち、質点ｍ₁、ｍ₂、ｍ₃、・・・が自由に動き得る“質点系の重心”は、各瞬間毎に上記の式にしたがって定義される点であるとする。その時には、重心は重力の合力の着力点としての意義を失い単なる“質量の中心”を意味する。

　物体の質量が連続的に分布している場合には、前記のΣは体積積分に置き換えればよい。すなわち、場所（ｘ，ｙ，ｚ）に於ける密度をρ（ｘ，ｙ，ｚ）とすると

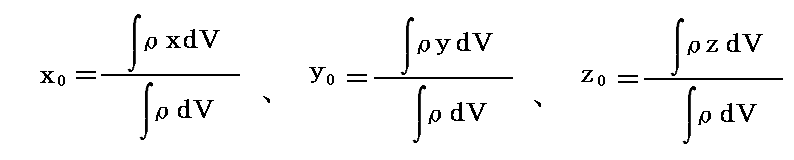
となる。
　特に密度ρが場所によらず一定の場合には、密度ρは積分記号の前に出せて分母分子で約される。そのため

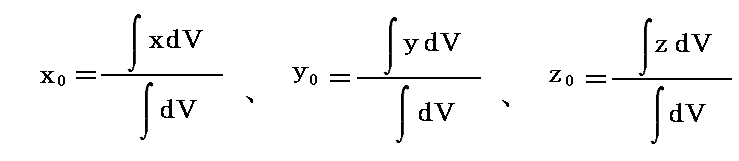
となる。
　立体の重心と同じく、平板状物体や線状物体の重心についても同様に計算すればよい。

［例題１］
　平板状物体の重心の例として、半径ａ、開き角αの扇形の重心を計算してみる。
　ｘ，ｙ座標を下図の様に取り、ｒ、θの極座標を用いる。

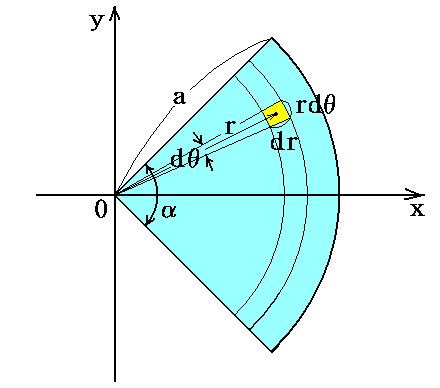
ここで積分はｒについては0→ａ、θについては−α／2→α／2まで行う。
　そうすると、重心座標（ｘ₀、ｙ₀）は

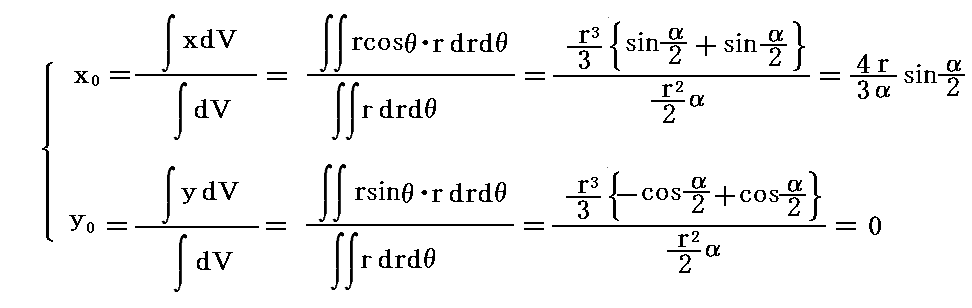
となる。
　α＝2πの場合には全円となり、重心座標は（ｘ₀、ｙ₀）＝（0，0）となる。またα→0の無限に狭い三角形の場合は、（ｘ₀、ｙ₀）＝（2ｒ／3，0）となる。

（３）平行で向きが反対の二力の合力

１．二力の大きさが異なる場合

　二力が平行かつ反対向きで、しかもその大きさが異なる場合の合力を求める。下図の様に着力点ＡとＢに働く二力Ｆ₁とＦ₂（ただしＦ₁＞Ｆ₂とする）の合力を求める。

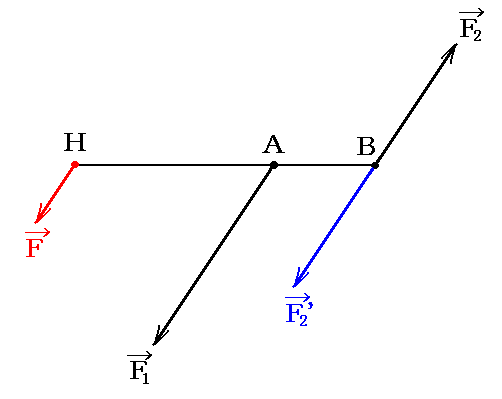
　大きい方の力Ｆ₁を、２．（２）１．の手順を逆に適用して、二つの平行かつ同じ向きの力に分解する。その内の一つは点Ｂに作用し、Ｆ₂と大きさ等しく向きが反対のＦ₂’とする。他方はＡから見てＢの反対側のある点Ｈに作用するＦとなる。このときＦの大きさはＦ＝Ｆ₁−Ｆ₂となる。
　二力Ｆ、Ｆ₂’とＦ1の着力点間距離には２．（２）２．で証明した関係が成り立たねばならないので

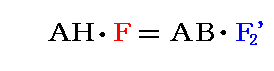
となる。
　今、力Ｆ₁の代わりにこの二つに分解した力を用いれば、Ｂ点にある二つの力Ｆ₂とＦ₂’は互いに消えてしまう。そのため、結局のところＦ₁とＦ₂の合力としてはＨ点に働く力Ｆのみが得られる。その大きさはＦ＝Ｆ₁−Ｆ₂であり、その方向はＦ₁の方向と一致する。またその着力点ＨはＡＢ間にはなくて、Ｆ₁の側外にある。すなわち

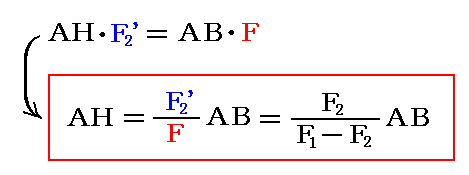
である。
　これは２．（２）２．で証明した関係

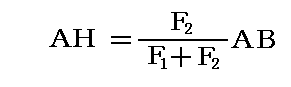
を一般化したもので、このＦ₂を負（つまりＦ₁の反対向き）に取ればよいのである。そうするとＡＨは負になるが、それはＨがＡから見てＢと反対側にあることを示している。
　高校物理では点ＨをＡＢの“外分点”であると説明するが、プランクのこの説明の方が解りやすい。また、この表現の方が多数の力の合力を求める場合には都合がよい。［次章３．（１）１．参照］。

［例題２］
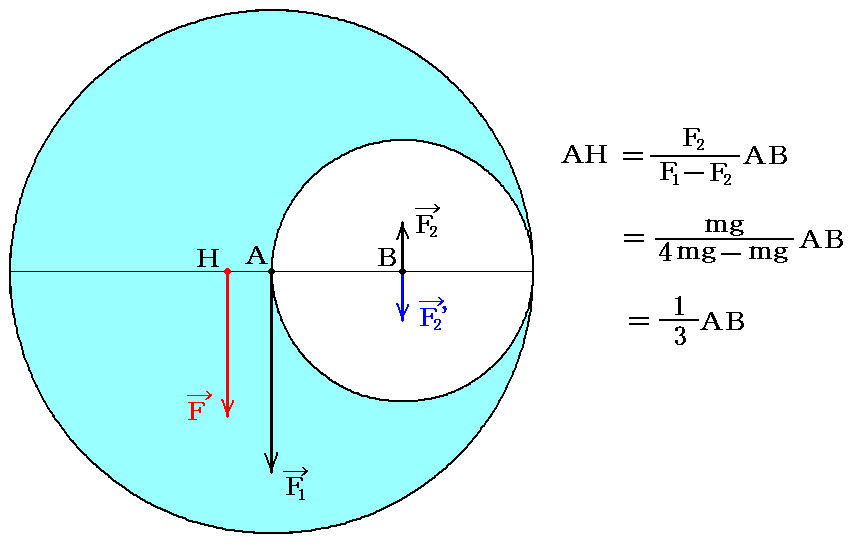
　ここの結論を用いると、下図の様なくり抜かれた円盤の重心は簡単に求まる。
　もし円板がくり抜かれていないとすると、その円板とくり抜かれた部分を構成する小円盤の質量比は、４対１となる。それは円の半径比が２対１であり、円盤の面積がπｒ²で計算できるからです。そのため、くり抜かれた部分の質量をｍとすると、問題の図形の質量は３ｍとなる。
　くり抜かれた状態の円盤の重心の位置をＨとするとそこに働く重力はＦ＝３ｍｇであり、くり抜かれた部分が元の位置にそのまま存在するとすると、それの重心はＢ点であり、重力はＦ₂’＝ｍｇとなる。
　この二つの重力の合力は、円盤の対称性より、Ａ点に働くＦ₁＝４ｍｇの重力となるはずです。これらの関係を、上記の説明と比較すると明らかなように、くり抜かれた円盤に働く重力の合力Ｆと、その着力点Ｈは、図中のＡ点に作用する力Ｆ₁＝４ｍｇとＢ点に作用する上向きの力Ｆ₂＝ｍｇの合力を求めれば求まる。
　

２．二力の大きさが等しい場合

　前項のＦ₂の大きさがＦ₁の大きさに近付くと、点Ｈは点Ａから次第に遠ざかって行く。そして、両者の大きさが等しくＦ₁＝Ｆ₂になると、合力の作用点は無限の彼方となり、その合力を定めることはできなくなる。一般に二つの大きさ等しく反対向きを持つ平行な力は、一つの合力にすることができない。この特別な形の力を“偶力”（あるいは“力対”）と言う。
　その性質はかなり込み入っているので、章を改めて詳しく考察する。

３．偶力のモーメント

（１）平行な多力の系

　前章で述べたように、平行であって、その向きが同じ、あるいは反対向きの多くの力が一つの剛体に作用するときには、一般にただ一つの力に合成することができる。
　もし剛体の各部分に働く力が互いに平行でない場合には、それぞれの力を三次元直交成分に分解すれば、それぞれの成分に対応する力の集合体は、全て平行な力と見なすことができる。そのため、互いの力が平行でない多力系については、三方向のそれぞれの成分に分解して、互いに平行となった一方向の力の系について考察すればよい。そして最後にそれら三方向の力の合力を合成すればよい。
　ただし、それら三方向の成分を持つ力系の合力については後ほど４．（１）で考察する事として、ここでは平行な多数の力からなる系の性質をもう少し調べてみる。

１．ΣＦ_i≠0　の場合

　前章で証明したように、互いに平行であってその向きが同じもの、または反対のものの多くの力が一つの剛体に働くとき、ΣＦ≠0ならば、それらの力をただ一つの力にすることができる。
　２．（２）と（３）で説明した平行な力の合成法則を利用して、２．（２）３．で行った様に個々の力を順番に加え合わせてゆけば良い。そのとき反対向きの力についてはΣの中の符号を負に変えて和を取る。そうすると、合力の着力点の位置座標は

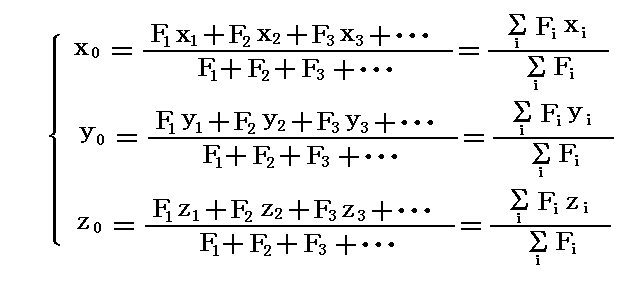
となる。
　また、合力の大きさは、各力の大きさの総和となり

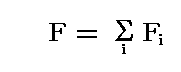
となる。
　この様に、ΣＦ_i≠0である限り合力の大きさと合力の着力点を求めることができる。静力学の問題としてはこれでお仕舞いで、後はこの合力が剛体にどの様な運動を引き起こすかという動力学の問題となる。

２．ΣＦ_i＝0　の場合

　前項の式に於いて

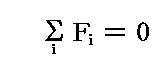
の場合には、合力の着力点（ｘ₀，ｙ₀，ｚ₀）を定める前記の公式が使えない。分母がゼロになって着力点の座標は無限遠となり、公式は意味を失ってしまう。
　この場合の多力は“平衡状態にある”か“一つの偶力（力対）”になる。

　ΣＦ_i＝0の場合、全ての力を二つに分ける。その一方はある同じ向きに作用する力で、これらをＦ₁’、Ｆ₂’、Ｆ₃’、・・・で表し、その合力をＦ’とする。他方はそれと反対の向きに作用する力でこれらをＦ₁”、Ｆ₂”、Ｆ₃”、・・・（これらを正にとる）で表し、その合力をＦ”とする。
　そのようにすれば、仮定により

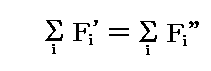
となる。
　そして、それぞれのグループの合力の着力点の座標は

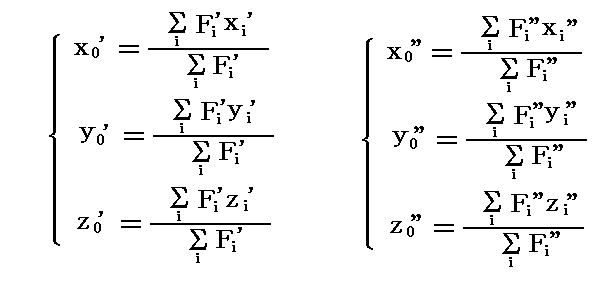
となる。

　このとき、大きさ等しくて方向が反対である二つの合力Ｆ’とＦ”の着力点を結ぶ直線がその力の方向と一致している場合には、当然のことながら二つの合力Ｆ’とＦ”は互いに打ち消し合って“平衡状態”となる。
　その時には、互いに反対向きの合力Ｆ’とＦ”の着力点である（ｘ₀’，ｙ₀’，ｚ₀’）と（ｘ₀”，ｙ₀”，ｚ₀”）を結ぶ線分と合力Ｆ’とＦ”の作用線が一致しているので、力の方向余弦を（α，β，γ）とすると

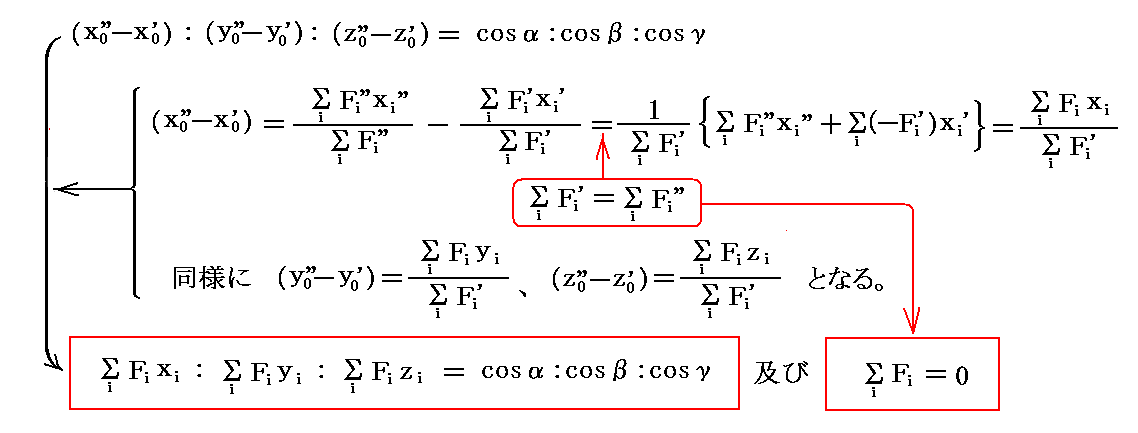
となる。
　これが平行にして方向が同じ、あるいは反対向きの多数の力が作用している力系が平衡になるための必要・充分条件です。
　例えば、力がｚ軸に平行又は反平行なときはα＝π／2、β＝π／2、γ＝0であるから、平衡条件は

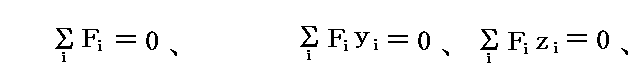
となる。

　大きさ等しくて方向が反対である二つの合力Ｆ’とＦ”（Ｆ’とＦ”の大きさは等しい）の着力点を結ぶ直線が合力の作用線と一致していないときには２．（３）２．で導入・定義した“偶力（力対）”となる。
　この場合にはさらに詳しい考察が必要なので節を改めて説明する。　

（２）偶力（力対）の性質

　大きさ等しくて方向が反対である二つの合力Ｆ’とＦ”の着力点を結ぶ直線がその合力の方向と一致していないときには“偶力（力対）”となる。
　互いに平行にして方向が反対な二力Ｆよりなる偶力の平面を図の面とする。このとき、二つの力のベクトルと、それらの力の着力点を結ぶ線分が直交していないときには、１．（２）で述べた法則にしたがつて、一つの力Ｆの着力点をその力の方向に移動させて、二つの着力点Ａ、Ｂを結ぶ直線がＦと直角を成すようにする。その様にすることは常に可能なので、今後はこのタイプの偶力について考察する。このとき線分ＡＢを“偶力のアーム”と言う。

１．着力点の移動

　一つの偶力は、その物理的意義を変化することなく力の方向に移動（例えばＡ’Ｂ’へ）させることができる。

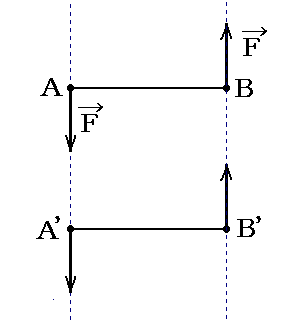
［証明］
　下図のようにＡ’点に新たな力の対ＦとＦ’を考える。このときＦとＦ’の大きさは等しく向きは反対に取る。この両者は互いに打ち消し合うのでその様にすることは常に可能です。

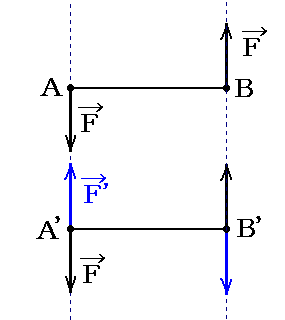
　そのとき、１．（２）で注意した理由により、Ａ点のＦとＡ’点のＦ’は互いに打ち消し合うので、結局Ａ’点の力Ｆのみが残る。Ｂ点とＢ’点についても同様に考えればＢ点に働く力ＦをＢ’点に働く力Ｆに置き換えることができる。
［終わり］　

２．アームの移動

　一つの偶力は、その物理的意義を変化することなく、アームＡＢの方向に移動（例えばＡ’Ｂ’へ）させることができる。

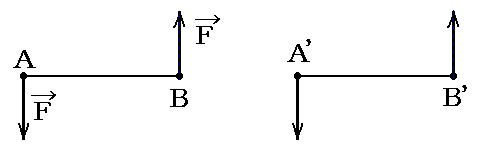
［証明］
　下図のようにＡ’、Ｂ’点に新たにＦとＦ’の力の対を考える。この両者は互いに打ち消し合うのでその様にすることは常に可能です。

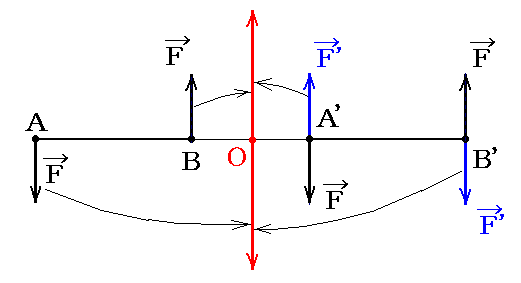
　次にＡ点のＦとＢ’点のＦ’、またＢ点のＦとＡ’点のＦ’を２．（２）で証明した法則により合成する。それら合力はＯ点に於いて互いに打ち消し合う反対向きの二つの力となる。そのため、Ａ点のＦ、Ｂ’点のＦ’、Ｂ点のＦ、Ａ’点のＦ’の四つの力は互いに打ち消しあって消えてしまい、Ａ’点のＦとＢ’点のＦのみが残る。つまりＡＢに於ける偶力をＡ’Ｂ’に於ける偶力に置き換える事ができる。
［終わり］　

３．アームの回転

　一つの偶力は、その物理的意義を変化することなく、アームＡＢの方向を偶力の面内に於いて任意に回転”（例えばＡ’Ｂ’へ）させることができる。

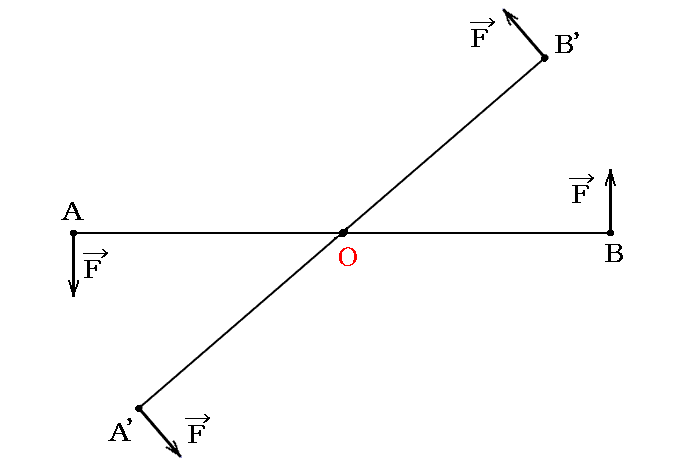
このとき、証明を読めば明らかなように、アームの回転は偶力面内に制限されねばならない。

［証明］
　下図のようにＡ’、Ｂ’点に新たにＦとＦ’の力の対を考える。この両者は互いに打ち消し合うのでその様にすることは常に可能です。

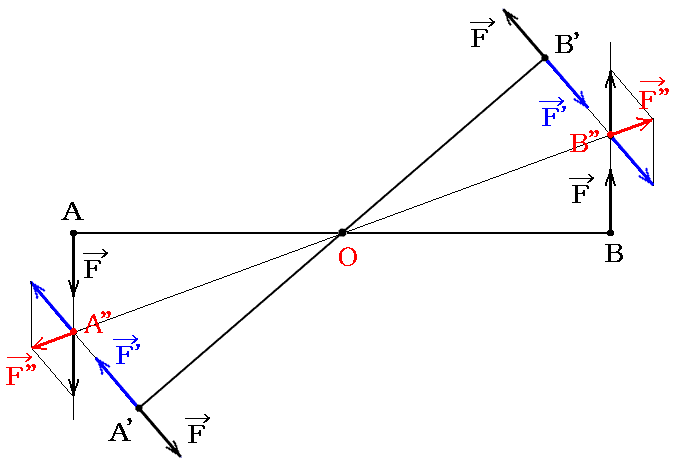
　次にＡ点のＦとＡ’点のＦ’を合成するとＡ”点に於ける合力Ｆ”となる。またＢ点のＦとＢ’点のＦ’を合成するとＢ”点に於ける合力Ｆ”となる。Ａ”点とＢ”点の二力Ｆ”は互いに同じ大きさで方向が反対なので打ち消し合う。そのためＡ点のＦ、Ａ’点のＦ’、Ｂ点のＦ、Ｂ’点のＦ’の四つの力は互いに打ち消しあって消えてしまい、Ａ’点のＦとＢ’点のＦのみが残る。すなわち、ＡＢに於ける偶力をＡ’Ｂ’に於ける偶力に置き換える事ができる。
［終わり］　

４．平行な平面への移動

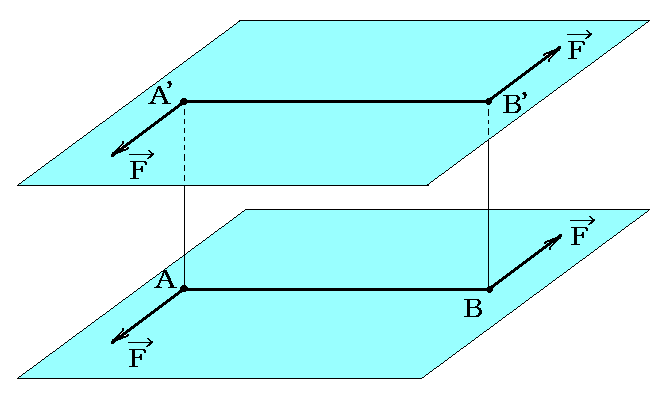
　一つの偶力は、その物理的意義を変化することなく、元の偶力が存在する面に平行な他の平面に移動（例えばＡ’Ｂ’へ）させることができる。

［証明］
　下図のようにＡ’、Ｂ’点に新たにＦとＦ’の力の対を考える。この両者は互いに打ち消し合うのでその様にすることは常に可能です。

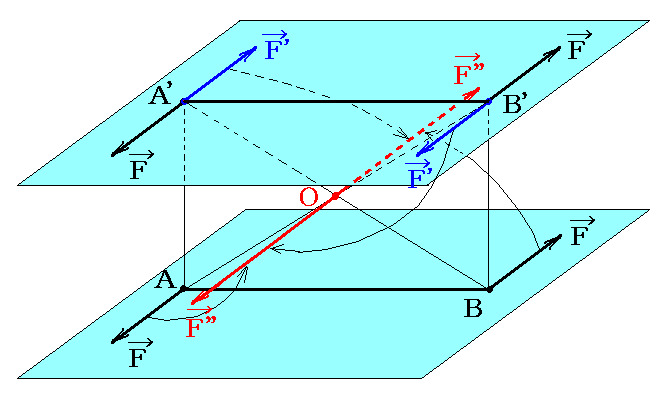
　次に、Ａ点のＦとＢ’点のＦ’を合成するとＯ点に於ける合力Ｆ”となる。またＢ点のＦとＡ’点のＦ’を合成するとＯ点に於ける合力Ｆ”となる。Ｏ点の二力Ｆ”は互いに同じ大きさで方向が反対なので打ち消し合う。そのためＡ点のＦ、Ｂ’点のＦ’、Ｂ点のＦ、Ａ’点のＦ’の四つの力は互いに打ち消しあって消えてしまい、Ａ’点のＦとＢ’点のＦのみが残る。すなわちＡＢに於ける偶力をＡ’Ｂ’に於ける偶力に置き換える事ができる。
［終わり］　

５．アームの長さの変更

　一つの偶力は、その物理的意義を変化することなく、アームＡＢの長さをアームの方向に変化（例えばＡＢ’へ）させることができる。ただし、このときアームの両端に働く力の大きさは変更を受ける。

［証明］
　今Ｂに作用する力ＦをＡとＢ’に作用する二つの平行な力に分解する。

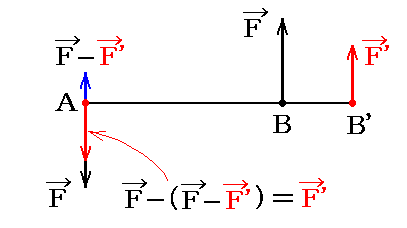
このとき、２．（２）２．の法則から、Ｂ’点に働く分力Ｆ’とＡに働く分力（Ｆ−Ｆ’）について

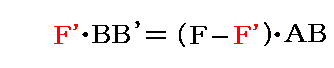
の関係が成り立つ用にすればよい。そのとき、Ｂ点の力Ｆは消えて、Ａ点にＦ−（Ｆ−Ｆ’）＝Ｆ’の力があり、Ｂ’点にはそれと大きさ等しく方向が反対の力Ｆ’が存在することになる。その二つで偶力（力対）をなし、そのアームはＡＢ’である。
　ここで、上記の式を用いると

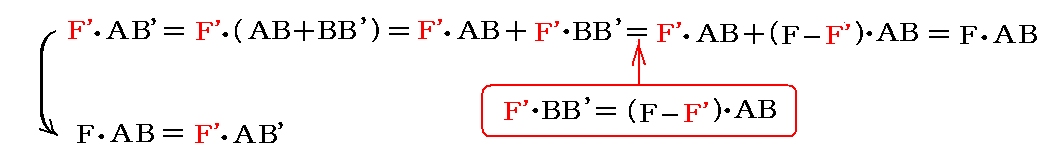
となる。すなわち力とアームの長さとの積が常に一定になるようにすれば、アームの長さは任意の長さに変化できる。
　ここで［力］×［アームの長さ］を“偶力（力対）のモーメント”と言う。つまり、モーメントが等しければ、同じ平面内あるいは互いに平行な平面内に在る二つの偶力（力対）は等しい。
［終わり］　

（３）偶力のモーメント

　前節で明らかになった偶力（力対）の性質から、偶力は下記の三つの量で定められると言える。

1. 偶力はその［モーメントの大きさ］＝［力の大きさ］×［アームの長さ］に依って定められる。
2. 偶力は力とアームが存在する平面の方向に依って定められる。
3. 偶力には向きが付随する。これは
   
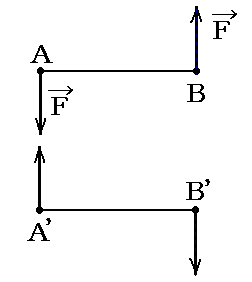
   の二つの偶力（力対）が同じ平面内にあり同じモーメントであっても、互いに平衡することから、両者が異なるとしなければならないからです。
   　普通、偶力の向きは、偶力が存在する平面に立てた垂線の向きで区別する。偶力の方向に右ネジを回転したときネジが進む方向を“偶力の向き”とする。

　以上の特徴から“偶力のモーメント”は下図の様な一つの矢印Ｍで表される。

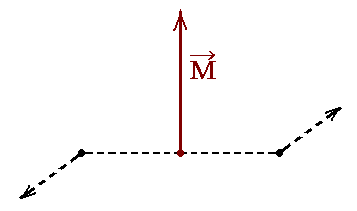
　矢印の長さはモーメントの大きさに等しく、その方向は偶力を構成するアームと力対が作る平面に垂直で、右ネジが進む方向です。このとき矢印Ｍの出発点を偶力の“作用点”と呼ぶことにする。
　この表示法による矢印は、前項の考察から明らかなように、長さと方向を変えなければどの場所へも移動させることができる。
　つまり、“偶力（力対）の“作用点”は、力の“着力点”と異なって、物理的な意味を持っていない”。これは究めて重要な性質です。

（４）偶力（力対）の合成

１．偶力のモーメントＭ₁、Ｍ₂、Ｍ₃、・・・が互いに平行な軸を持つ場合

　全ての偶力モーメントが平行な場合、３．（２）で述べた偶力の性質により、全ての偶力を唯一つの平面上に移し、しかも共通なアームを持つようにできる。

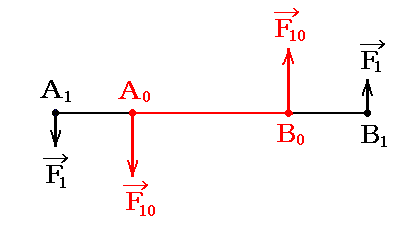
　そのとき共通アームＡ₀Ｂ₀の両端に働く力の大きさは、３．（２）５．で述べたように、以下の関係式を満たすように決めればよい。

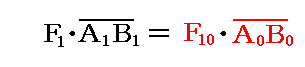
つまり、上式を満たす大きさＦ₁₀にすればよい。
　同様にＭ₂、Ｍ₃、・・・を同じアームＡ₀Ｂ₀に移すと、それらの力Ｆ₂、Ｆ₃、・・・は

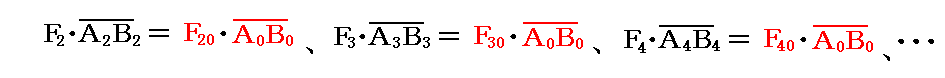
の関係を満たすＦ₂₀、Ｆ₃₀、・・・に変換すればよい。
　そのため合成された偶力のモーメントは、Ａ₀端又はＢ₀端で加え合わされた力　Ｆ₁₀＋Ｆ₂₀＋Ｆ₃₀＋・・・にアームの長さＡ₀Ｂ₀を乗じたものになる。
　これは結局

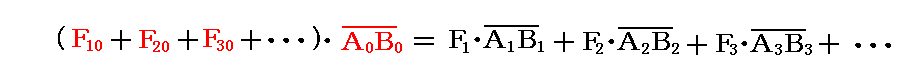
と同じ事を言っているので、合成されたモーメントＭの大きさは、各モーメントＭ₁、Ｍ₂、Ｍ₃、・・・の大きさの和で表されると言っても良い。
　つまり合成モーメントは、個々のモーメントの軸と同じ方向を向き、その長さが個々のモーメントの長さの和になる矢印で表される。

２．偶力のモーメントＭ₁、Ｍ₂が任意の角をなし、かつ交わらない場合

　この場合でも二つのモーメントＭ₁とＭ₂の矢印に垂直な平面は必ず互いに交わる。そのため３．（２）に説明した性質に従い、二面の交線上に共通のアームＡ₀Ｂ₀を取ることができる。

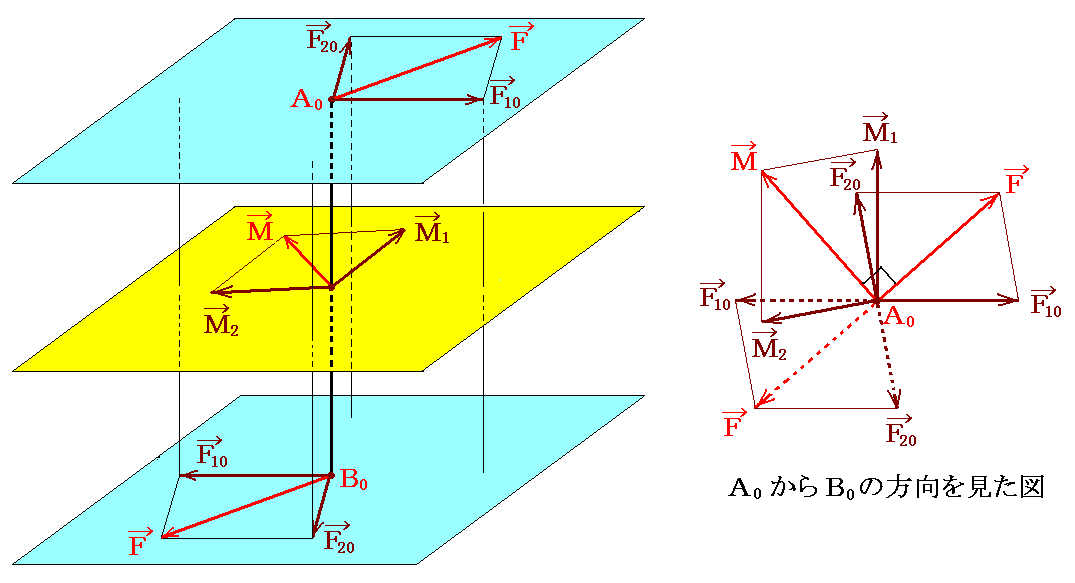
　ここで、アームの長さを共通にするために、前項と同じように、それぞれの偶力を表す力は調整される必要がある。つまり

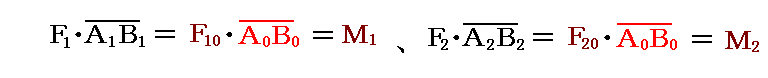
としてある。そのとき［モーメントの大きさ］＝［力］×［アームの長さ］は、たとえ［力］と［アームの長さ］が変わっても不変であることに注意。
　このときＦ₁₀とＦ₂₀はＡ₀及びＢ₀点に於いて力の平行四辺形の法則によって合成できる。このときそれぞれの偶力のモーメントを表すＭ₁もＭ₂はそれぞれの力が存在する面に垂直であって、かつ

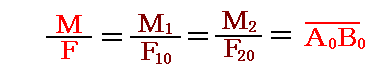
となるので、Ｍ₁とＭ₂に依って描かれた四辺形も平行四辺形となる。さらに、その平行四辺形は力Ｆの平行四辺形に相似であって、唯その位置を90°だけ回転したものになる。
　それゆえに、“偶力（力対）”を表すのに前に述べた“矢印Ｍ”を用ることにすれば、“偶力は“ベクトル”であって、力と同じように“平行四辺形の法則”によって合成または分解できる。”

３．偶力ベクトルの合成

前項１．と２．の結論から以下のことが言える。

　剛体に様々な偶力Ｍ₁、Ｍ₂、Ｍ₃、・・・が働く場合には、ベクトルの加法に依って一つの合成偶力Ｍとする事ができる。それぞれの偶力の作用点が異なる場合には、３．（３）の法則に従って、それらを全て同一の点に移動させてベクトル合成する。
　すなわち

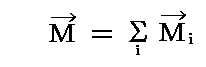
となる。
　その作用点を原点にとり、それぞれの偶力ベクトルの方向角を（λ₁，μ₁，ν₁）、（λ₂，μ₂，ν₂）、・・・・、及び（λ，μ，ν）とすると、偶力ベクトルの成分表示は

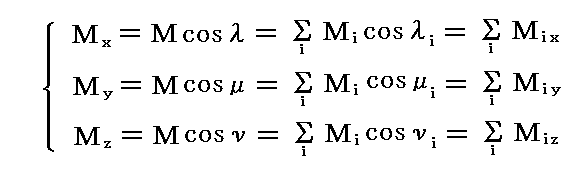
となる。

４．任意の力の合成

（１）任意の多力系の合成

１．力の着力点の移動とモーメント

　任意の力（二つの力が平行ではないが、さりとてその作用線が一点で交わることがない、つまり作用線が三次元空間内で同一平面上になくて、すれ違っている場合を含む）については、２．（１）１．で後で説明することを予告しておいた。ここでその約束を果たします。
　その作用線が互いにすれ違っている二力を合成するとき必要なのは以下の法則です。

　剛体中の着力点Ｐに働く一つの力Ｆは、Ｐ以外の任意の点Ｏに於ける力Ｆと偶力（力対）Ｍに置き換えることができる。

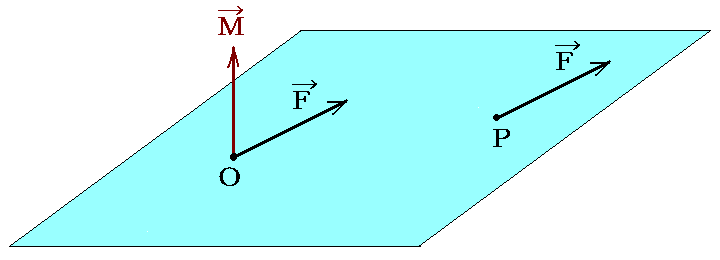
　そのとき、モーメントＭの軸は、必ずＯＰＦ面に垂直となり、線分ＯＰからベクトルＦの方向に右ネジを回したときネジの進む方向を向いたベクトルとなる。

［証明］
　Ｏ点に於いて力Ｆと、それと大きさ等しく向きが逆の力−Ｆの対になる力を考える。両者は互いに打ち消し合うのでその様にすることは常に可能です。

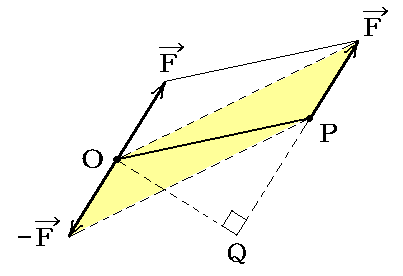
　その様にすればＰ点に働く力ＦはＯ点に働く力Ｆと偶力Ｍで置き換えることができる。［偶力Ｍのモーメントの大きさ］＝［Ｆの大きさ］×［Ｏから初めの力Ｆの作用線に至る垂直距離ＯＱ］であって、それは図中で黄色に着色した平行四辺形の面積です。
　今後、この大きさＭ＝［Ｆ］×［ＯＱ］の事を“点Ｐに作用する力Ｆの点Ｏ関するモーメント”と言うことにする。そのとき、モーメントＭの軸は、必ずＯＰＦ面に垂直となり、線分ＯＰからベクトルＦの方向に右ネジを回したときネジの進む方向を向いたベクトルとなる。もし点Ｏを力のＦの作用線上に取ると、そのモーメントは0となる。
［終わり］

２．任意の多くの力の合成

　前項の法則を用いれば、一つの剛体に働く任意の方向を向いた任意の数の力Ｆ_iを合成することができる。
　すなわち、全ての力を前項４．（１）１．の方法で一つの共通な着力点（例えば座標原点）に移して、そこでそれらの力の合成力Ｆ＝ΣＦ_iを作る。
　そのときなお、それぞれの力の移動に伴って前項で説明した偶力（力対）Ｍ_iが生ずるが、それも“合力の着力点（例えば座標原点）”を“作用点”とする偶力（力対）とすることができる。それらの偶力を３．（４）３．の方法でベクトル的に合成して１つの偶力（力対）Ｍ＝ΣＭ_iとすればよい。
　結局、一つの剛体に働く任意の力系は、在る一つの着力点に働く合成力Ｆと合成偶力（力対）Ｍにすることができる。　

（２）ベクトル表示

前節の合成力、合成偶力（力対）を具体的に求めるには、ベクトルの成分表示を利用して計算するのが便利です。

１．座標成分表示

　原点から距離ｒの点Ｐ（ｘ，ｙ，ｚ）に於ける力Ｆ＝（Ｆx，Ｆy，Ｆz）を座標原点に於ける力Ｆと偶力（力対）Ｍ＝（Ｍx，Ｍy，Ｍz）で表してみる。

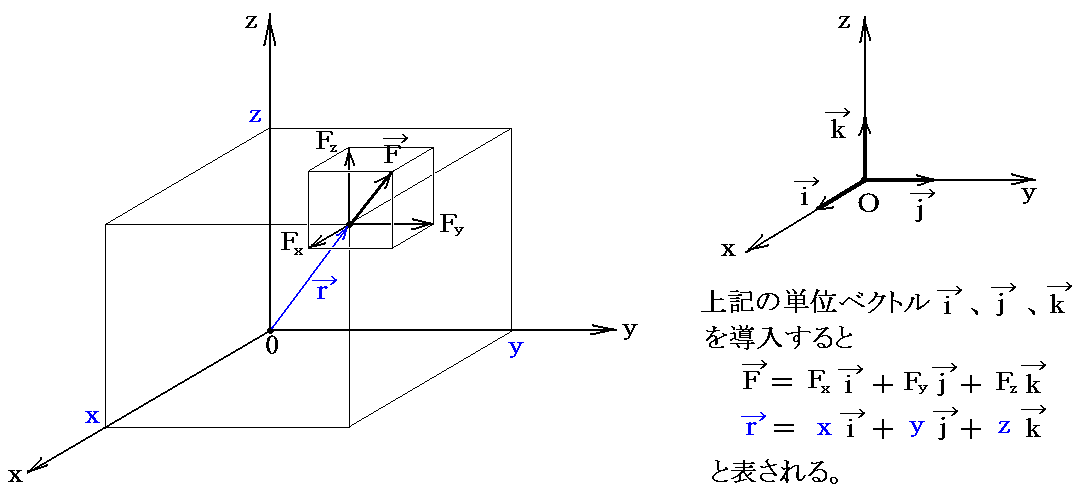
　まず、上図に於いて着力点ｒの力Ｆ_ｚを原点Ｏに移すときに発生する偶力（力対）を考えてみる。図のようにＦ_ｚをＢ点に移動し、Ａ点とＯ点にＦ_ｚの大きさで互いに反対向きのペアの力を考える。それらの力は互いに打ち消し合うので、その様にすることは常に可能です。

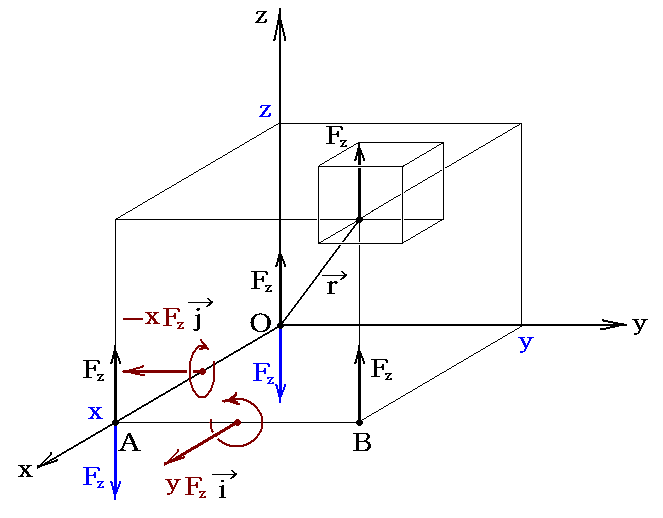
　このときＡ点の力Ｆ_zとＢ点の力Ｆ_zはｘ軸の正方向を向く偶力（力対）を生じる。そのモーメントはＡＢ・Ｆ_z＝ｙＦ_zとなる。全く同様にして、Ｏ点の力Ｆ_zとＡ点の力Ｆ_zはｙ軸の負方向を向く偶力（力対）を生じる。そのモーメントはＯＡ・Ｆ_z＝ｘＦ_zとなる。つまり、Ｐ点のＦzをＯ点に移すとｘ成分がｙＦ_z、ｙ成分が−ｘＦ_zの二つの偶力（力対）モーメントベクトルを生じる。
　全く同様な議論をＰ点に働く力Ｆx、Ｆｙについて行えば、結局Ｐ点に働く“力のベクトルＦ”をＯ点に移すと、それに伴ってｘ，ｙ，ｚ成分が

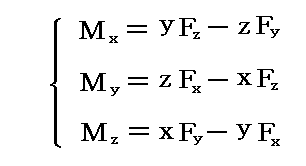
となる“偶力（力対）のモーメントベクトルＭ”が生じることになる。このとき、３．（３）で述べた“偶力（力対）の作用点は任意の場所に移動できる”という法則を利用した。

　このとき、上記の成分表示で表されるベクトルＭは、位置ベクトルｒと力のベクトルＦが作る平面に対して垂直で、しかもｒからＦへ右ネジを回したときにネジの進む方向を向いたものになる。
　また、ベクトルＭの大きさは、ベクトルｒとベクトルＦが作る平行四辺形の面積［ ｒＦsinθ (ここでθはベクトルｒとベクトルＦの成す角)］となる。

［証明］
　証明は別稿「ベクトルの内積(スカラー積)と外積(ベクトル積)の成分表示」２．(４)を参照。
［終わり］

　ｒとＦの二つのベクトルの成分より構成される上記のベクトルＭをベクトルｒとベクトルＦの“外積（ベクトル積）”と言い

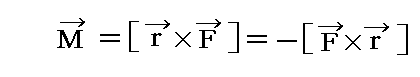
で表す。ただし、普通の掛け算と混同する恐れが無いときには鉤括弧［　］を省略して単に　Ｍ＝ｒ×Ｆ＝−Ｆ×ｒ　と表すことにする。

２．外積ベクトルを用いた表現

　外積ベクトルを用いれば、一つの剛体の着力点ｒ₁、ｒ₂、ｒ₃、・・・に任意の方向を向いた力Ｆ₁、Ｆ₂、Ｆ₃、・・・が働くとき、それらの力系は座標原点に作用する唯一つの力Ｆと唯一つの偶力(力対)Ｍとすることができる。すなわち

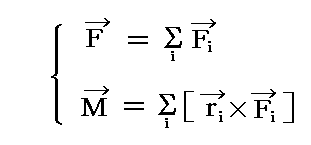
である。このとき、Ｆ＝ΣＦ_iは、それぞれのベクトルを座標原点に移動させて加え合わせたものであり、Ｍの外積表現中のベクトルｒ_iは、（力のベクトルＦ_iを移動・集約した点を座標原点とする）移動前の力のベクトルＦ_iの着力点の“位置ベクトル”です。

　また、この表現を用いれば

　一つの剛体に作用する力系が平衡を成すための必要充分条件は、その合成力Ｆと合成偶力(力対)Ｍが共に0となることです。すなわち

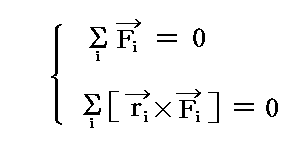
である。これは各力のｘ，ｙ，ｚ成分と、力の着力点の座標成分で表される６つの条件式となる。
　このときＦ＝ΣＦ_i＝0で在ってもＭ＝ΣM_i＝Σ［ｒ_i×Ｆ_i］＝0と成ることは保証されない事に注意。平衡であるためには両方の条件が必要です。

　普通これらは、“力のつり合いの法則”と“力のモーメントのつり合いの法則”と言われる。

（３）合力の着力点の移動

　前節では、力のベクトルＦ_iを移動・集約した点を座標原点として論じたが、その移動・集約点を別の点に移すとどの様な事が生じるか考察する。

１．予備的考察

　全力系の合成力Ｆと合成偶力（力対）Ｍが点Ｏに働いているとする。これをＯ以外の任意の点Ｏ₀に移すと、それぞれのベクトルはどの様になるかを考察する。４．（１）の考察から明らかなように、合力ＦはそのままＯ₀点へ移動できる。その時Ｆの移動に伴って新しい偶力（力対）Ｍ’が生じる。この軸はベクトルＦと線分ＯＯ₀がなす平面に垂直で、それは元々存在するＭと合成されて偶力（力対）ベクトルＭ＋Ｍ’≡Ｍ₀となる。
　このようにしてＯ点の合力Ｆと偶力ＭはＯ₀点での合力Ｆと偶力Ｍ₀になるのであるが、このとき元々在るＭと新しく生じるＭ’が互いに打ち消し合ってＭ₀＝０となる様なＯ₀点は存在するであろうか？

　残念ながら一般的にＭ₀＝０となる様な点は存在しない。ただし、Ｍ＋Ｍ’≡Ｍ₀の軸が常に合力Ｆの方向に一致する様にできる点Ｏ₀は存在する。それは次のようにすればよいのである。
　下図のように偶力Ｍを合力Ｆに平行な成分Ｍ_ｐ（parallel　平行の）とそれに垂直な成分Ｍ_ｒ（rectangular　直交の）に分解する。そしてベクトルＦとベクトルＭ_ｒに垂直な方向にＯから距離Ｍ_ｒ／Ｆ　離れた点をＯ₀とする。その方向はＭ_pからＭ_ｒの方向に右ネジを回したときにネジの進む方向にとる。そのときＯ₀点にＦと−Ｆの対になる力を考える。両者は互いに打ち消し合うので、その様な力の対を置くことは常に可能です。

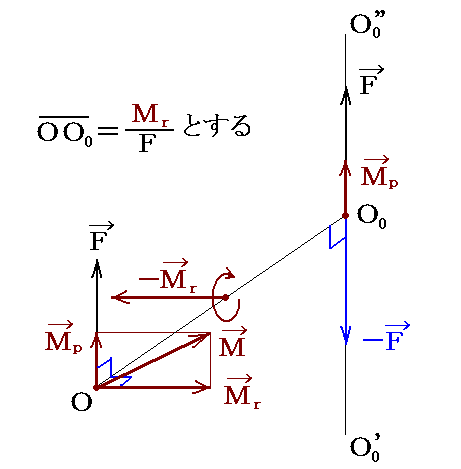
　そうすると、Ｏ点の力ＦとＯ₀点の力−Ｆが一つの偶力ベクトル−Ｍ_rとなる。なぜなら線分ＯＯ₀の長さをＭ_ｒ／Ｆ　としているので、［偶力のモーメントの大きさ］＝Ｆ・（Ｍ_ｒ／Ｆ）＝Ｍ_ｒ　となるからです。このようにして新たに生じた−Ｍ_rと元々在ったＭ_rは互いに打ち消し合うので、結局Ｏ₀点の力Ｆと偶力Ｍ_ｐのみとなる。
　このときＯ₀を図中の直線Ｏ₀’Ｏ₀”上のどこに取っても力や偶力は同じなので、直線Ｏ₀’Ｏ₀”上ならどこに移動しても同じ状況が実現できることに注意。

　４．（２）２．で証明したように、一つの剛体に作用するいかなる力系も一つの合力と一つの合成偶力（力対）となるのだが、このときさらに合力の“着力点”を適切に選べば、合成偶力（力対）Ｍ＝ΣM_i＝Σ［ｒ_i×Ｆ_i］の軸が合力Ｆ＝ΣＦ_iの方向に一致するようにできる。

２．一般的考察

　点Ｏ₀を前項で説明した点とする。すなわち、その点に於いて合力Ｆの方向と合成偶力Ｍ₀の軸が一致している。今度はこの点の力Ｆを他の任意の点Ｏに移すことを考える。その点Ｏは、取りあえずＯ₀を通り力Ｆや偶力Ｍ₀に垂直な平面πの上に取るとする。
　そのとき新たな点ＯにＦと−Ｆの対になる力を考える。両者は互いに打ち消し合うので、その様な力の対を置くことは常に可能です。

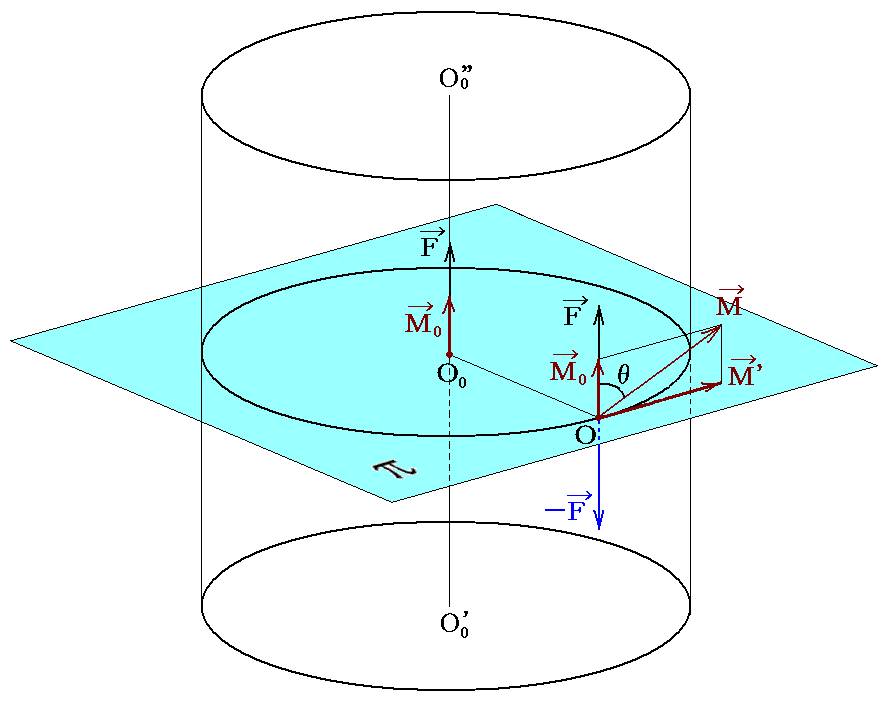
　そうすると、４．（１）の考察と同様にして、Ｏ₀の力ＦとＯ点の力−Ｆは一つの偶力となる。それをＭ’とする。そのとき、元々存在する偶力Ｍ₀も新たに生じた偶力Ｍ’も、３．（３）で説明したように、その“作用点”を自由に移動できるので新たな点Ｏに移動する。そうするとＯ点に合力Ｆと合成偶力Ｍ₀＋Ｍ’≡Ｍが存在することになる。
　このときＯ点に現れた合成偶力モーメントＭの大きさは

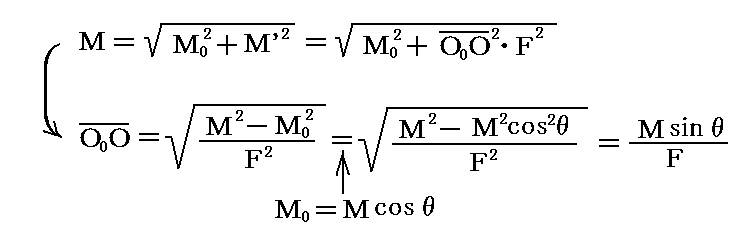
となり、この軸は線分Ｏ₀Ｏに垂直な面内に在って合力Ｆと角θをなす。そのとき、θは

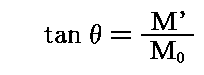
なる関係を満足する。
　さらに、Ｏ点をＯ₀を中心とする円周上の点とすれば、Ｏがその円周上の何処にあっても、Ｍ’、Ｍ、θは一定である。このとき円周の半径であるＯ₀Ｏ間の距離を大きくすれば、それに従ってＭ’、Ｍは限りなく大きくなりθは限りなくπ/2に近付く。
　以上の事情はπ平面上の円周上での話しに限らない。Ｏ点を図中に示したＯ₀’Ｏ₀”を中心線とする円柱面上の任意の点に移動しても同様な事が言える。合力Ｆも合成偶力Ｍも“合成力Ｆの作用線”上を移動させても物理的な意味は変わらないからです。このとき、Ｏ₀点を通り、上記円柱の中心線を構成する線分Ｏ₀’Ｏ₀”の事を力系の“中心軸”という。
　これらの事実から、結局

　剛体に働く任意の力系の合成力Ｆ＝ΣＦ_iと合成偶力Ｍ＝ΣM_i＝Σ［ｒ_i×Ｆ_i］は４．（２）２．の方法で求める事ができるのだが、このとき合力の“着力点”Ｏをさらに移動（Ｏ₀へ）させて適切に選べば、その移動に依って生じる合成偶力（力対）Ｍ₀の軸が合力Ｆの方向に一致するようにできる。このとき合成偶力（力対）の大きさは最小値となる。
　その位置での合力Ｆの作用線を“中心軸”というが、その向きは元の合力Ｆの方向と一致し、その場所は元の合力ベクトルＦと合成偶力ベクトルＭが作る面に垂直で、ＦからＭへ右ネジを回したときにネジの進む方向に、点Ｏから距離

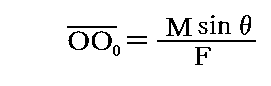
だけ離れた場所となる。ここでのθは元の合成ベクトルＦと合成偶力ベクトルＭが成す角度です。その中心軸に現れる新しい偶力（力対）ベクトルの大きさはＭ₀＝Ｍcosθとなる。

３．特別な場合の例

［例１．Ｍ₀＝ΣM_i＝0の場合］
　この場合には中心軸上の偶力は常に0であって、力系の合力は中心軸上の一点に作用する力Ｆ＝ΣＦ_iのみになる。
　そのとき、力Ｆの作用点を前項で説明した任意の半径の円筒面上に移動すると、新しく発生する偶力Ｍ＝ΣM_iはＭ’のみとなり、合成力Ｆと合成偶力Ｍ＝Ｍ’は常に直交する。
　このことを逆に解釈すれば、力系が唯一つの力のみに合成できるための必要充分条件は合成力ΣＦ_iと合成偶力ΣM_iが互いに垂直であることが解る。つまり

　合成力ΣＦ_iと合成偶力ΣM_iが互いに垂直である場合、すなわち

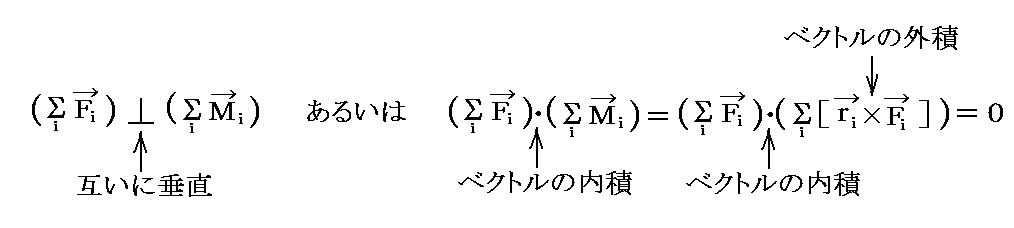
が成り立てば、合力Ｆの“着力点”を適切に選ぶことによって合成偶力（力対）Ｍを0にすることができる。
　別稿「ベクトルの内積(スカラー積)、外積(ベクトル積)の成分表示」１．(５)で証明したように、二つのベクトルが直交すれば、二つのベクトルの内積がゼロとなることに注意。

［例２．Ｆ＝ΣＦ_i＝0の場合］
　この場合には、中心軸は意味を成さない。力系は唯一つの定まった合成偶力Ｍのみとなり、その“作用点”は任意に取ることができる。

［例３．Ｆ＝ΣＦ_i＝0かつＭ₀＝ΣM_i＝0の場合］
　このときには平衡する場合であり、“座標原点”の選び方は全く考えなくて良い。

（４）制限された運動自由度を持つ剛体

　４．（２）２．で述べた平衡の為の条件は自由に運動する剛体に関するものです。もし剛体の運動が外部からの束縛力に依ってある制限を受けているときには４．（２）２．で述べた条件は平衡の為の充分条件ではあるが必要条件ではない。幾つかの重要な例について、平衡のために如何なる条件が必要なのか調べてみる。

１．剛体内の一つの直線が固定しているとき。

　このときは固定されている直線をｚ軸にとり、その力系を原点に作用する合成力Ｆとそれに対応する偶力（力対）Ｍとにする。今それが平衡であるためにはＦ＝0である必要はない。なぜならば原点に於いてｚ軸上の各点に作用するのと同じく、束縛力が作用していて、その束縛力はそれらの点に於いて作用する動力と全ての状態のもとで消し合っているからである。
　次に偶力（力対）について考えるに、例えば偶力の成分の一つＭ_xはｙ軸の方向を持っている互いに反対な二つの力から成り立っていて、その二つの力はｚ軸上の点に作用しているから外からの束縛力に依って打ち消されている。同様にＭ_yの力はｘ軸の方向を持っていてｚ軸上の点に作用する様にすることができるから、これも又束縛力と消し合っている。唯Ｍ_zのみがｚ軸上の束縛力による影響を受けない。
　そのため平衡であるための必要充分条件は

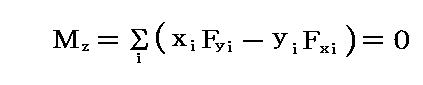
となる。これが、剛体が平衡であるために、動力の成分とその作用点の座標との間に成り立つ事が必要な唯一つの式である。Ｍ_z≠0のときには、剛体はｚ軸の回りに回転する。

　この場合には、４．（２）２．で述べた条件の残りの５つの式は、固定している軸が作用しているはずの抵抗力を見いだすのに必要な式となる。この抵抗力は自由に運動することのできる軸を静止させる為に外から作用すべき束縛力である。この束縛力は条件式に従って、動力の影響をちょうど打ち消す様に作用する。つまり、この束縛力は原点に於いて作用する力−Ｆと、−Ｍ_x及び−Ｍ_yとより成る一つの偶力（力対）と等しい。
　ｚ軸を固定するには、その上の二点を固定すれば充分であるから、束縛力は常にこの二点に作用する二つの力に帰す事ができる。

２．剛体がｚ軸の回りに回転できるが、この軸に沿って滑る事ができる場合。

　この場合には平衡であるためには前項の条件に付け加えて

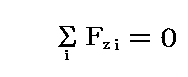
なる条件が必要である。なぜなら、このとき束縛力はｚ軸の方向には働かないからです。
　物体が自由に運動し得る程度が多いほど、まはたその束縛が少なければ少ないほど、平衡が実現するために動力が満足しなければならない条件の式が多くなる。

３．剛体が固定した一点の回りに自由に回転できる場合

　この点を座標原点Ｏに取る。このときはＯに作用する合力Ｆ＝ΣＦ_iと束縛力とが互いに消し合う。そのため剛体が平衡であるための必要充分条件は

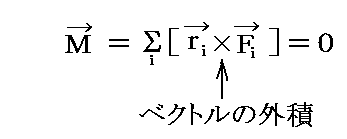
となる。これは動力の成分と、その着力点の座標との間の三つの関係式である。
　このような物体は三つの自由度を持っている。もしＭ≠0ならば動力に依ってＯ点の回りの回転運動を起こす。

５．参考文献

　剛体に働く力の合成・分解は高校生に取って解りにくい所です。
　高校物理の教科書では、最初に“力のモーメントの定義”を教えて、“力のモーメントのつり合いの法則”（梃子の原理はその特別な場合）を導入します。そして、“力のモーメントのつり合いの法則（力のつり合いの法則に対応）”を使って
　（１）二力が平行でない場合。
　（２）二力が平行で同じ方向を向いている場合。
　（３）二力が平行で反対を向きしかも大きさが異なる場合。
　（４）二力が平行で反対向きでしかも大きさが同じ場合（偶力）。
に分けて剛体に働く力の合成・分解を説明します。
　しかし、多くの教科書の論理展開はかなりいい加減です。
　
　この稿では参考文献１．に従って“力のつり合いの法則”から始めて剛体に働く力を一般化しました。その一般化の過程で“偶力”や“力のモーメント”を導入し、最後に“力のモーメントのつり合いの法則”を導きました。このやり方なら、互いにすれ違う力の合成も容易に理解することができます。
　
　上記のやり方のどちらが良いのか意見が分かれる所ですが、私自身はプランクの説明の方がより厳密な論理展開がやりやすいように思います。
　なぜなら、高校物理教科書のやり方では力のモーメントの作用点が何を意味するのか全く不明ですが、プランクのやり方では合力Ｆ＝ΣＦ_iの着力点を決めることで合成偶力（力対）Ｍ＝ΣＭ_i＝Σ［ｒ_ｉ×Ｆ_i］やその作用点に明確な意味を持たせることができるからです。

1. マックス・プランク著、寺沢寛一、久末啓一郎訳　理論物理学汎論第一巻「一般力学」裳華房(1926年刊)原本初版は1916年の発刊
   　ここでは、第�U篇第１章§76〜§91の内容をほぼそのまま紹介しています。
2. エルンスト・マッハ著「マッハ力学−力学の批判的発展史」講談社（1969年刊）第�T章