マックス・プランク(河井徳治訳)「現代物理学の思想(上)」−講演と回想− 法律文化社(1971年刊)P169〜187 より引用
これはとても難解な文章で、原論文とつきあわせながら読まないと理解は難しいのですが、熟読する価値があります。前半は自らの作用量子の導入についての説明であり、後半は量子論の当時の成果と課題の説明です。1918年度のノーベル賞ですが、受賞の決定は1919年11月13日で、講演がなされたのは1920年6月2日です。量子力学の全体が明らかになる1926年以前の、1920年であることを考慮すると、その内容はとても興味深い。
この中の輻射公式の内挿式の解釈についての説明は別稿「作用量子発見の歴史によせて」の方がより詳しい。また内挿式へ至るエントロピーに関する考察は両方で強調されている。両方を合わせて読まれることを奨めます。
[段落分、題目、文字の着色・強調等は、読みやすくするために当方が適当に行いました。また文中の(古典論文叢書No)は物理学史研究刊行会編「物理学古典論文叢書1 熱輻射と量子」東海大学出版会(1970年刊) の中の論文番号を意味します。]
マックス・プランク ノーベル賞講演 1920年6月2日
量子理論の起源と今日までの発展
私の著述に関連した公開講演をおこなうという義務が、本日私に課せられた思召しを正しく汲むなら、本財団の高潔な創設者に対する恩義というその意義を深く心に銘じながら、皆さんに量子論の成立史をかいつまんで述べるとともに、この理論の今日までの発展と、それが現に物理学に寄与している意義について簡単にスケッチする以外にはないと思う。
物理的作用量子の概念とその重要性が、はじめて現存する経験的事実の領域から明らかにされだして、すでにもう20年になるが、今日その歳月をふり返り、ついにはその発見に導いた永い、多岐にわたる錯綜した道程をかえり見るとき、私には時おり、この発展の全体が、人間は努力する限り誤るものであるという、あの真実を語ったゲーテの言葉の新たな例証のように思えるのである。
実際、勤勉な研究者の張りつめた精神労働は、彼がさまざまの試行錯誤の後に、ついにはやはり真理に向って、少なくともたしかに一歩を進めたのだということが、明白な事実によって時には動かしがたい仕方で証明されるのでなければ、結局はすべてが無駄で空しいものに思えるであろう。
もちろんその際一定の目標を追求しながら、当初の失敗によってもその照明力が曇らされないような、一定の目標を追求することは、それだけではまだ成果を保証するとは言えないまでも、その不可欠の前提であるに違いない。
1.量子の導入
(1)黒体輻射
私にとって、このような目標は、ながい間、輻射熱の正常スペクトルにおける、エネルギー分布の問題を解くことであった。グスタフ・キルヒホフが、熱の放出と吸収をおこないながら温度を一様に保っている、任意の物体によって境界づけられた空洞の中での熱輻射の性質は、その物体の性質にまったく無関係である[G.Kirchhoff, U¨ber das Verha¨ltnis zwischen dem Emissionsvermo¨gen und
dem Absorptionsvermo¨gen der Ko¨rper fu¨r Wa¨rme und Licht. Gesammelte
Abhandlungen, p597(§17). Leipzig: J. A. Barth 1882(古典論文叢書2)]ということを示して以来、温度と波長にのみ関わって、どの物質のいかなる特別の性質にもまったく関わることのない、ある普遍関数の存在が証示されていた。
そして、この注目すべき関数を発見することが、まさに熱力学と、従ってまた分子物理学全体の第一の課題を形成しており、エネルギーと温度との連関に対して、より深い洞察を約束していたのである。
その関数をうるための道すじとしては、自然界に見いだされるかぎりのさまざまな物体の中から、既知の放出能と吸収能をもっているものを選びだし、その物体と定常のエネルギー交換をするような熱輻射の性質を算定するという方法しかなかった。こうしてこの熱輻射の性質は、キルヒホフの命題どおりに、物体の性質には関係しないことが証明されなければならなかったのである。
この目的に、とりわけふさわしい物体のように私に思えたのは、ハインリヒ・ヘルツの線型振動子であるが、一定の振動数を与えた場合にそれが従う放出の法則は、ヘルツによってすこし前に、完ぺきに明らかにされていた[H. Hertz, Ann. d. Physik, Bd.36, p1, 1889]。
一定数のこのようなヘルツの振動子が、反射する壁にとり囲まれた空洞の中にあるとすれば、それはちょうど起音体と共鳴体とのように、電磁波の放出と吸収とによって、相互にエネルギーを交換するであろう。そしてついにはその空洞内に、キルヒホフの法則に一致する、定常の、いわゆる黒体輻射が生ずるに違いあるまい。
当時、私は古典的な電気力学の諸法則が、それを十分に一般的にとり扱って、あまりに特異な仮説を遠ざけてさえいれば、予想される事象の本質を把握し、それによって努力の目標を達成するのに十分だろうとの期待に、たしかに今からすれば、いささか無邪気に思えるほど頼りきっていた。
それゆえ私は、さしあたって線型共振子の放出と吸収に関する法則を、できるかぎり一般的な基盤の上で明らかにしてみたが、これは当時すでに基本的には仕上っていたH・A.ローレンツの電子理論を利用すれば省けたはずの、事実上の回り道であった。
しかし私は、電子の仮説にはまだ全幅の信頼を寄せていなかったので、共振子から適当な間隔をおいて、それを囲む球面上に出入りするエネルギーを考察するというやり方を選んだのである。その際、ただ真空中での事象だけを考察したが、共振子のエネルギー変化への必要な推論を導くためには、その知識で十分にこと足りた。
このかなりにわたる一連の研究は、それぞれが現今の諸観測、とりわけ、V・ビェルクネスの減衰測定との比較によって吟味され、またそのことによって確証された[Sitz.-Ber. d. PreuB. Akad. d. Wiss. vom 20. Februar 1896; Ann. d. Physik, Bd. 60, p577, 1897 に再録]のだが、その成果は、一定の固有周期をもった共振子のエネルギーと、周囲の場にあってそれに対応するスペクトル範囲のエネルギー輻射との、定常のエネルギー交換における一般的な関係を定めた[Sitz.-Ber. d. PreuB. Akad. d. Wiss. vom 18. Mai 1899, p455; Ann. d. Physik,
(4)1, p69〜122, 1900 に再録(古典論文叢書10)、これはSitzungsber. Berl. Akad. Wiss. に発表した一連の5編の論文1897(2/4、7/8、12/16)、1898(7/7)、1899(5/18)の最後のもので総まとめの論文です]ことであった。
その際、明らかになったのば、この関係が共振子の性質にまったく依存せず、とりわけ、その減衰定数にも依存しないという、まことに注目すべき結果であるが、これは私にとって非常に喜ばしい、好都合な事情であった。
なぜなら、そのことによって、輻射のエネルギーの代りに共振子のエネルギーをとることができ、こうしてまた多くの自由度からなる錯綜した系の代りに、唯一の自由度をもつ単純な系を当てうるということで、問題全体が簡単になったからである。
もちろん、この成果の意味するところは、今やまったく見当もつかない高さで、いっそうけわしくそびえたつことになった本来の課題に着手すべく、ほんの準備的な一歩を印したものにすぎない。
これを征服しようとする最初の試みは失敗に帰した。なぜなら、私がもともとひそかに期待していたのは、共振子から放出される輻射が何らかの特徴において吸収される輻射とは区別され、そのことからある微分方程式が立てられて、これを積分すれば定常の輻射の性質をきめる特殊な条件が得られるだろう、ということであったが、これは見事に裏切られたのである。
共振子は、自ら放出するのと同じ輻射にだけ反応して、近接するスペクトル範囲に対しては少しも感応しなかった。
そのうえ、共振子が、一方的な、それゆえ不可逆の作用を、周囲の輻射の場のエネルギーに及ぼしうるだろうとする私の臆測は、ルドヴィヒ・ボルツマンの激しい反駁をひき起す[L.Boltzmann, Sitz.-Ber. d. PreuB. Akad. d. Wiss. vom 3. Ma¨rz 1898, p182]ことになり、彼は自分のより豊富な経騒をもって、この問題に関し次のことを証明してみせた。
すなわち、古典力学の法則によれば、私の考察した事象のすべてはまさに反対の方向にも生じうるもので、つまり、共振子からいったん放出された球面波は、逆に外から内へと、絶えず縮小してゆく同心の球面となって共振子にまで収縮しつづけ、それによってふたたび吸収され、そのことによって他方また、以前に吸収したエネルギーを、それがやってきた同じ方向へと、共振子をしてふたたび空間内に送り出させるというのである。
私はこの内部に向う球面波という特異な事象を、自然輻射の仮説という特殊な制限的規定の導入によって排除することはできたものの、やはり、問題全体の中心点を完全に把握するには、なお本質的な連環項が欠けているに違いないことが、分析を進めるにつれてだんだんと明らかになった。
(2)内挿式の導出
かくして私は、問題を一度反対側から、つまり、そうでなくても最初からそのほうが確実な基盤だと感じていた、熱力学から手がけてみるほかはなかった。共振子の温度ではなくて、エントロピーをそのエネルギーと関係させよう、しかも、エントロピーそのものをではなく、エントロピーのエネルギーに関する第二次微係数を関係させよう、なぜなら、これこそが共振子と輻射の間のエネルギー交換の不可逆性に対して、直接の物理的な意味をもつのだからと、ためらわずにすぐ思いついたことによって、事実、ここで熱理論の第二主法則についての私の初期の研究が役立つことになった。
それにもかかわらず、私はその頃まだあまりにも現象論的な傾向にあり、エントロピーと確率の関連をつきつめて問うことができなかったので、当座はただ、現にある経験の成果だけを頼りにしているありさまであった。
さて、1899年の時期に最も注目をあつめていたのは、すこし前にW・ヴィーンによって立てられたエネルギー分布法則[W. Wien, Ann. d. Physik, Bd. 58, p662〜669, 1896(古典論文叢書6)]であったが、これを実験的に吟味する仕事は、一方ではハノーファー工科大学のF・パーシェンによって、また他方ではシャルロッテンブルク国立研究所のO・ルンマーとE・プリングスハイムによって着手されていた。
この法則は輻射強度の温度に対する関係を、一つの指数関数によって定めたものである。
共振子のエントロピーとエネルギーの間の関係をそれに従って計算してみると、先に述べた微係数の逆数、それを一応ここではRと呼ぶことにするが、これがエネルギーに比例するという、注目すべき結果が明らかになる。
[ヴィーンのエネルギー分布法則によれば、共振子のエネルギーUの温度に対する関係は
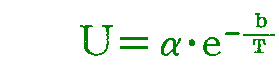
である。従って共振子のエントロピーをSとすれば、
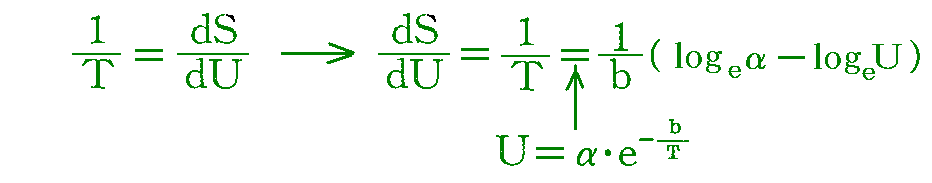
であるから、量Rの値は
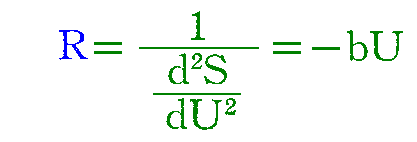
となる。]
このきわめて簡単な関係は、ヴィーンのエネルギー分布法則の完ぺきな表現とみなすことができる。というのは、エネルギーに対する関係とともに、波長に対する関係までが、一般に保証されているヴィーンの変位則によって、いつでも直ちに与えられるからである。
[ヴィーソの変位則によると、固有振動数νをもった共振子のエネルギーUは、
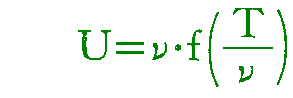
となる]
問題は要するに普遍的な自然法則を求めることであり、また当時私は、今もってそうであるように、自然法則というものが、一般的であればあるほどより簡単に表現されると考えていた。
もちろんその場合、いかなる公式化がより簡単なものとみなされるべきかは、必ずしも明確にかつ決定的に断ぜられうる問題ではないにしても、とにかく、そういう見解をかたく抱いていたので、一時私は、Rの量がエネルギーに比例するというこの命題に、エネルギー分布法則全体の基礎を認めるべきだと信じていた。[Ann. d. Physik, (4)1, p719〜737, 1900(古典論文叢書11)]
しかし、この考えは、やがてより新たな測定の結果と対立して、根拠のないものだということが判ったのである。
というのは、小さな値のエネルギーについて、つまり短い波についてなら、ヴィーン法則はどこまでも見事に実証されたのであるが、比較的長い波については著しい偏差が、O・ルンマーとE・プリングスハイムによってはじめて確認され[O.Lummer und E. Pringsheim, Verhandl. d. Dtsch. Physik. Ges. Bd. 2, p163, 1900]、さらにまた、H・ルーベンスとF・クールパウムが螢石と岩塩の残留赤外線でもっておこなった測定[H.Rubens und F. Kurlbaum, Sitz.-Ber. d. PreuB. Akad. d. Wiss. vom 25.
Oktober 1900, p929]は、この二つの量の間にまったく異なった、しかも同じようにふたたびきわめて簡単にもなる関係を明らかにした。
それは、Rの量がエネルギーにではなく、エネルギーの平方に比例し、しかもエネルギーと波長を大きくとるほど、その比例の精度は高くなるという関係である。
[何となれば、H・ルーベンスとF・クールバウムの実験では、大きいTに対しては U=cT であり、従って従って共振子のエントロピーをSとすれば、
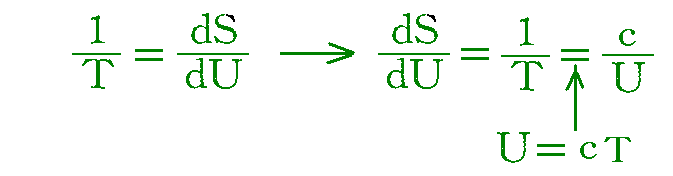
であるから、量Rの値は
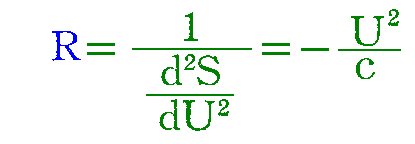
となる]
さて、このように直接的な経験をとおして、関数Rには、比較的小さいエネルギーに対する比例関係と、大きいエネルギーに対するその平方についての比例関係という、二つの簡単な極限が定められた。それゆえ、まったく自明のことながら、これを一般化するには、Rの量を、エネルギーの一乗をもつ項と二乗をもつ項との和に等置し、小さいエネルギーには第一項が、大きいエネルギーには第二項が決定的となるようにすればよく、それによって新たな輻射公式が得られたが、
[つまり、
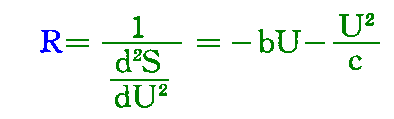
とおけば、積分して
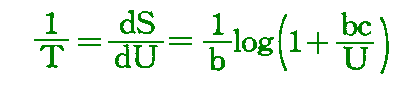
となる。それゆえ輻射公式は
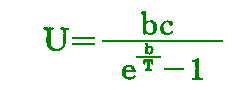
となる。Verhandl. d. Dtsch. Physik. Ges. vom 19. Oktober 1900, p202 を参照(古典論文叢書12)]
これは今日に至るまで、かなり十分にその実験的吟味に耐えている。経験を通じての、究極的で厳密な実証については、もちろん今でもまだ云々することはできないが、新たな吟味はむしろ切望されるところでもあろう[W. Nernst und Th. Wulf, Verhandl. d. Dtsch. Physik. Ges., Bd. 21, p294, 1919]。
(3)内挿式の物理的意味
しかしながら、たとえこの輻射公式が絶対に正確だと保証されるにしても、それはただうまくあたった内挿式だという意味で、あくまでもまったく制限された価値をもつにすぎないだろう。従って私は、この式を立てたその日から、それにほんとうの物理学的な意義を付与するという課題に没頭したのであり、そしてこの問題は、私をおのずからエントロピーと確率の関係についての考察に、こうしてまた、ボルツマンの思考過程へと導くことになった。私の生涯で最も緊張した研究作業の数週間がたって、ついに暗闇はしらじらと明け、新しい、思いもかけなかった遠景が姿を見せはじめた。
ここに、ちょっとした注釈をはさませていただきたい。エントロピーは、ボルツマンによれば、物理的な確率に関する一尺度であり、従って、熱理論の第二主法則の本質は、ある状態の確率が高ければ高いほど、それはよりひんぱんに自然界に生起する、ということにある。
ところで、直接に測定されるのは、いつもただエントロピーの差であって、けっしてエントロピーそのものではないから、その限りでは、ある種の専断をもってでなければ、ある状態の絶対的なエントロピーについて語るわけにはゆかない。しかしながら、適当に定義されたエントロピーの絶対的な値は、それによっていくつかの一般的な命題が特に簡単に公式化されることがある以上、その導入はむしろ当をえていよう。
私の見る限り、この事情はエネルギーについてもまったく同様である。エネルギーも、それ自身が測定されるのではなく、その差が測定されるにすぎない。
だから、以前はエネルギーで計算せず、仕事で計算したし、またエネルギー保存の法則をさまざまにとり扱っていながら、観測の領域を越えるいっさいの思弁には原則として立ち入らなかったエルンスト・マッハは、エネルギーそのものを論ずることを常にまた避けていた。
同様に熱化学においても、特にヴィルヘルム・オストヴァルトが、熱量計の数値の代りに、エネルギーそのもので計算すれば、かなりの煩雑な考察が本質的に省かれることを強調するまでは、はじめはいつでも、実熱量に、従ってエネルギーの差にとらわれつづけていた。
エネルギーそのものを表わすについても、はじめはまだ不確定の付加定数が残っていたが、エネルギーと慣性との比例関係についての相対論的な命題によって、のちにはこれが究極的に確定されるにいたった[何となれば、エネルギーの絶対値は、慣性質量と光速度の平方との積に等しい]。
エネルギーといっしょに(より適切にはむしろ、温度といっしょに)、同時にまたエントロピーも消去されるといったことで、この付加定数が定まるのだから、エネルギーに対してと同じように、いまやエントロピーにも、従ってまた物理的な確率にも、ある絶対的な値を定義することができるわけである。
そのような考え方にもとづいて、共振子の系内における一定のエネルギー分布の物理的な確率を計算するために、輻射法則によって条件づけられたエントロピーを正確に表現しうるような、ある一定の比較的簡単な組合せの扱い方が明らかになった[Verhandl. d. Dtsch. Physik. Ges. vom 14. Dezember 1900, p237(古典論文叢書13)]。
そしてルドヴィヒ・ボルツマンが、私の論文の送付にたいする返信の中で、私のうち出した考え方に興味と原則的な同意を打ち明けてくれたことは、さんざんに経験した幻減の代償としては特に価値あるものを私にもたらした。
(4)二つの普遍定数
そのような確率の考察を数量的に実行するためには、二つの普遍定数を知る必要があったのであるが、それらはいずれも独立の物理的な意味をもっているゆえ、輻射法則からそれらを補足的に算定するならば、こういった一連のやり方がたんなる計算上の技巧として評価されるべきか、それとも、そこには実際に物理学的な意義が含まれているのかという問題は、それによって検証の手がかりを与えられることになる。[Ann. d. Physik Bd. (4)4, p553〜563, 1901(古典論文叢書14)]
第一の定数kは、かなりフォーマルな性質のものであって、それは温度の定義と関連している。かりに、温度を理想気体中の一分子がもつ平均の運動エネルギーとして、従ってきわめて徴小な量のものと定義すれば、この定数は、2/3の値をもつことになろう[kを第一の輻射定数とすれば、気体分子の平均運動エネルギーは一般に、U=3/2kTであることから、T=Uとおけば、k=2/3となる。ところで通常の(ケルヴィンの絶対)温度目盛りでは、Tは沸騰するときと、氷結するときの水の温度差が100に等値されることで定義されている]。
ところが通常の温度目盛を用いれば、この定数の値は、ある極端に小さいものとなるが、それは当然ただ一つの分子のエネルギーと密接に結びついており、従ってその正確な知識は分子の質量と、またそれに連関するもろもろの量の算定に導くのである。
この定数は、しばしばボルツマンの定数とも呼ばれているが、私の知る限り彼自身がそれを導入したことはけっしてない。むしろ折にふれての彼の発言から推測されるように[たとえば L.Boltzmam, Zur Erinnerung an Josef Loschmidt. Popula¨re Schriften,
p245, 1905 を参照]、ボルツマンはその定数が正確に測定できるなどとは思ってもいなかったのだから、これはまことに奇妙なことであると言ってもよかろう。
それ以来、たった一つの分子の質量を天体のそれとほとんど同じ精度で測定する方法が、一、二にとどまることなく発見されたという事実は、この20年間における実験技術の大躍進を、たしかに最もよくもの語るものであろう。
私が輻射法則からのこの計算をおこなっていた時期には、得られた数値を精密に検証することはまったく不可能であり、たかだかその数位の正しさが確認できるくらいであったが、その後しばらくして、E・ラザフォードとH・ガイガー[E. Rutherford und H. Geiger, Proc. Roy. Soc. A. Vol. 81, p162〜173, 1908]は、α粒子を直接数えることによって電気素量の値を、4.65×10-10静電単位と規定することに成功し、それが私の計算した数値である4.69×10-10と符合したことは、私の理諭の有効性に対する決定的な証明とみなされえたのである。
その後さらにねり上げられた、E・レゲナー、R・A・ミリカン[R.A.Millikan, Phys. Ztschr., Bd.14, p796, 1913]などの方法によって、この値はもう少し大きく定められることになった。
輻射法射の第二の普遍定数hは、最初の計算では、6.55×10-27erg・secとなり、エネルギーと時間の積をあらわしたので、私はそれを要素的作用量子と名づけたが、これを解釈することは第一のそれに比べてはるかにやっかいであった。
それがエントロピーの正しい表現をうるためには絶対に欠かせないものであり、実際、ここに試みられた確率の考察は、その基準となる「基礎領域」、つまり確率の「演域」の大きさを、それによってはじめて定められる[何となれば、ある物理的な状態の確率を計算することは、当の状態が等しく実現しうる、有限数の個々の場合を数え上げることにもとづき、これらの個々の場合をはっきりと境界づけるには、あらゆる個々の場合の概念をはっきりと確定する必要がある]にもかかわらず、これをなんらかの適当な形で古典理論の枠に合わせようとするあらゆる試みは、どこまでも強くはばまれていることが明らかになった。
それが無限小のものとみなされうる限りでは、つまり大きいエネルギー、すなわち長い周期の場合には、すべてはきわめてうまく片づいたが、一般化すると、どこかに破綻が現われ、しかもそれは、より小さくより速い振動を問題にすれぼするほど、ますます目立つものとなった。この破綻をつくろおうとするいっさいの試みが失敗に帰したことは、やがてまったく疑いを残さぬところとなった。
作用量子は虚構の量にすぎず、輻射法則の演繹全体が原理的に錯覚であり、たんに無内容な公式のもてあそびを演じただけであったのか。
それとも、輻射法則が導かれたことの根底には、ひとつの真に物理学的な思想があり、作用量子のはたすべき役割りは、物理学の基礎にかかわるものであって、つまりそこには、ライプニツとニュートンが微積分を創始して以来、あらゆる因果連関の連続性という仮定の上に築かれてきたわれわれの物理学的な思考を、その根底からくつがえす使命を授かったかに見えるような、まったく新たなもの、今まで耳にしたこともないものが出現しているのだろうか。
経験は、この二者択一の後者をとった。しかし、その決定がこのようにはやく、またこのようにきっぱりと下されたことを、科学は熱輻射のエネルギー分布法則についての検証にではなく、いわんやこの法則に私が与えた特殊な演繹にでもなく、ひとえにただ作用量子を活用した研究者たちが、たゆみなくおし進めた仕事に負うているのである。
2.量子論の成果
この領域での先駆者となったのは、A・アインシュタインである。彼は一方では、光の作用に関する一連の注目すべき観察、つまりストークスの法則や電子の放出、気体のイオン化といった事柄について簡単な説明をうるためには、作用量子によって条件づけられたエネルギー量子の導入が適当であることを示唆し[A. Einstein, Ann. d. Physik, Bd.17, p132, 1905]、また他方では、共振子の系のエネルギーに対する表現を、そのまま固体のエネルギーにも当てはまるものとすることによって、固体の比熱の推移、とりわけ温度が下る際におけるその低下を、全体として正しくとらえた公式を導きだしている[A. Einstein, Ann. d. Physik, Bd.22, p180, 1907]。
それとともに、さまざまな方向でいくつかの問題が提起されたが、それらのより厳密で多面的な徹底した研究は、時がたつにつれて、数多くの貴重な資料を明るみにだしてきた。そこに示された数々の業績のすべてにわたって、ほんのひととおりの報告をすることも、ここでは私の課題でなかろうから、進歩してゆく認識の過程における、最も重要で特徴的な諸段階だけを問題にすればよいだろう。
まず熱および化学の事象をとりあける。固体の比熱に関しては、原子の唯一の固有振動を仮定することにもとづくアインシュタインの考察が、M・ボルンとTh・v・カールマンによって、異なった種類の固有振動という現実によりよく合致する場合にまで拡張された[M. Born und Th. v. Ka´rma´n, Phys. Ztschr. Bd.14, p15, 1913]。
またP・デパイは、固有振動の性質に関する前提を大胆に単純化することによって、固体の比熱について比較的簡単な公式をたてることに成功した[P. Debye, Ann. d. Physik, Bd.39, p789, 1912]が、それはとりわけ低い温度に対して、W・ネルンストとその弟子たちが測定した値と見事に一致するだけではなく、物体の弾性的および光学的な諸性質ともうまく調和するものである。[このことについては、別ページ引用のSommerfeldの解説も参照されたし]
ところで気体の比熱に関しても、作用量子は注目される。すでに早くからてW・ネルンストが、振動のエネルギー量子には、回転のエネルギー量子も対応するはずだと示唆していた[W. Nernst, Phys. Ztschr. Bd.13, p1064, 1912]ことから、気体分子の回転のエネルギーも、温度が下れば失われるものと期待されていた。水素の比熱についてのA・オイケンの測定は、この推論を実証した[A. Eucken, Sitz.-Ber. d. PreuB. Akad. d. Wiss. p141, 1912]ものであり、A・アインシュタインやO・シュテルン、P・エーレンフェストなどの計算が、これまで厳密には満足のできる一致を生みだしていないとしても、明らかにそれは水素分子の模型についての、われわれのまだ不完全な知識のせいである。
量子条件によって特徴づけられる気体分子の回転が、事実自然界に存在するということは、N・ビエルム、E・v・バール、H・ルーベンスおよびG・ヘットナーなどによる赤外線中の吸収帯についての仕事から、もはや疑うことはできない。もちろん、この注目すべき回転スペクトルを全面にわたって解明することは、今のところまだできてはいないのであるが。
また、物質の親和的な性質は、結局すべてそのエントロピーによって条件づけられているのだから、エントロピーの量子論的な計算は、化学結合論のあらゆる問題に対する入り口でもある。
気体のエントロピーの絶対値は、ネルンストの化学的定数によって特徴づけられており、O・ザックールはこれを直接に、私が振動子に用いたのと似たような組合せの扱い方によって計算した[O. Sackur, Ann. d. Physik Bd.36, p958, 1911]が、一方、O・シュテルンとH・テトローデは、測定から得られたデータにより密着して、気化過程に注目することにより、気状と固状におけるエントロピーの差を確定した[O. Stern, Phys. Ztschr. Bd.14, p629, 1913, H. Tetrode, Ber. d. Akad. d. Wiss. v. Amsterdam, 27. Februar und 27. Ma¨rz 1915]。
これまでみてきた場合に常に問題となっているのは、熱力学的な平衡状態であり、従って、計算はそれについて、多くの微粒子と比較的長い時間に関係する、たんに統計的な平均値を提示することができるにすぎなかった。
これに対して、電子の衝突を観察することは、探究される事象の力学的な明細へと直接にたち入るのであり、そのことによって、J・フランクおよびG・ヘルツは、電子が帯電しない原子に衝突するとき、これに光量子を放出させるために、少なくともそれが保有していなければならない臨界速度、つまりいわゆる共振ポテンシャルを確定することに成功しているが、これは作用量子を測定する上で、それ以上に直接的であることを望みえないような方法の一つである[J. Franck und G. Hertz, Verhandl. d. Dtsch. Phys. Ges. Bd.16, p512, 1914]。
C・G・パークラによって発見された、レントゲンスペクトルの特徴的な輻射を生ぜしめるのにも、D・L・ウェブスター、E・ヴァグナーなどの実験によれば、まったく一致する結果に至る同様の方法ができ上っている。
電子の衝突による光量子の発生に対して、光線、レントゲン線、ないしはガンマー線の照射による電子の放出は、これとは逆の過程である。ここでもやはり特徴的な役割りを演ずるのは、作用量子と振動の周波数とによって条件づけられるエネルギー量子であるが、そのことは、放出される電子の速度が、たとえば照射の強度にではなく[Ph. Lenard, Ann. d. Physik Bd.8, p149, 1902]、たんに当てられる光の色にのみ依存する[E. Ladenburg, Verhandl. d. Dtsch. Phys. Ges. Bd.9, p504, 1907]という特異な事実において、すでに早くから知られていた。
ところで、定量的な観点においても、先に触れたアインシュタインの光量子への示唆は、あらゆる角度から確証されており、とりわけR・A・ミリカンは、放出された電子の初速度の測定によってそれを確認した[R. A. Millikan, Phys. Ztschr. Bd.17, p217, 1916]し、また一方、光化学反応を導くために光量子がしめる意義については、E・ヴァールブルクがこれを明らかにした[E. Warburg, U¨ber den Energieumsatz bei photochemischen Vorga¨ngen in Gasen. Sitz.-Ber. d. PreuB. Akad. d. Wiss. von 1911 an.]。
たしかに、物理学のさまざまな領域から得られた以上の経験は、こぞって作用量子の存在のために、強力な証明材料を提供してはいるにしても、量子仮説がその最も堅固な基盤を獲得したのは、なんといっても二ールス・ポーアによる原子理論の基礎づけとその形成によってであった。というのは、この理論の役割りは、スペクトル分析が発見されて以来のあらゆる試みにもかかわらず、頑として開こうとしなかった分光学という不思議の国への扉に対し、久しく求られていたその鍵を、作用量子の中に見いだすという仕事であったが、それがひとたび道を通じてからは、この領域のすべてにわたって新しく得られた認識が、物理学と化学の隣接諸領域にまでも、大洪水のように流れこんだのである。
その最初の輝かしい成果は、水素とヘリウムに対するバルマー系列の公式をひき出したことであるが、それはまた、リュードベリの普遍定数を既知の数量だけに還元すること[N. Bohr, Phil. Mag. Bd.30, p394, 1915]をも含み、その際しかも、水素の場合とヘリウムの場合における僅かな相違は、重い原子核の微弱な運動によって必然的に生ずるものであることが認識された。
続いてはきわめて効果的でありながら、今はじめてその根本の意義が解明されたリッツの結合原理を用い、光学的スペクトルやレントゲンスペクトルにおける他の諸系列も探究されることとなった。
ところで、これらの分光学的な測定はとりわけ精密なものであったゆえ、このような数量的一致は特に決定的な証明力をもつと主張してもよかったわけだが、それにもかかわらず、なおも偶然のたわむれを信じたいと思ったかもしれない人にも、結局はやはり、最後の疑念を払いおとさざるを得ない時はきたのである。
それは、A・ゾンマーフェルトが、量子を分配する法則の解釈をいくつかの自由度をもった系にまで拡張し、かつまた慣性質量が相対性理論の要求するところに従って変化することを考慮すれば、水素スペクトルやヘリウムスペクトルについて、その徴細な構造の謎を明かさずにはおかない例の呪文(じゅもん)が得られることを示した[A. Sommerfeld, Ann. d. Physik Bd.51, p1, 125, 1916]時、しかもそのことが現在可能な限りでの最も精密な測定である、F・パーシェンの測定によって確認できた[F. Paschen, Ann. d. Physik Bd.50, p901, 1916]時であった。この業績は、海王星の存在と軌道要素を、だれもまだそれを見ない前に計算した、ルヴェリェの有名な発見にも十分に匹敵する。
同じ道をさらに進んで、P・エプスタインは、スペクトル線の電気的分岐という、かのシュタルク効果を完全に解明する[P. Epstein, Ann. d. Physik Bd.50, p489, 1916]ことに、P・デバィはまた、マンネ・ジーグバーンによって調べつくされた、レントゲンスペクトルのK系列を簡単に解釈することに成功した[P. Debye, Phys. Ztschr. Bd.18, p276, 1917]が、こうして、原子の構造の暗い秘密の内部を大なり小なり成功裡に照らし出した、一連の多くの研究がさらに進展したのである。
そのような成果を細大もらさず述べてゆくには、なおここで少なからぬ重要な名前を、どうしても引合いに出さねばならないだろうが、ともあれ、これらの成果をすべて見たあとでは、そうした事実のかたわらを素通りしようとする評者でない限り、あらゆる種類の多くの事象のどの一つにおいても、常に変らずほぼ6.54×10-27erg・secという同じ数値を示してきた作用量子[E. Wagner, Ann. d. Physik Bd.57, p467, 1918, R. Ladenburg, Jahrb. d. Radioaktivita¨t
u. Elektronik Bd.17, p144, 1920]が、物理的な普遍定数の体系への完全な市民権をもつと認める以外には、結論の出しようがない。
一般的相対性の思想が自由な軌道をうち開いて、思いもかけない成功にふみ出していたまさにその同じ頃に、またまさに最も期待のもてなかった当の場所で、自然がある絶対的なものを、つまりそれを用いれば、一つの時空成分の中に含まれる作用量が、完全に恣意を離れた一定の数値によって表わされ、それによって作用量のこれまでの性格が取り去られることになる、そういう実際に不変な単位尺度を開示したということは、おそらく不思議な符合のように思えるに違いない。
3.今後の課題
もちろん、作用量子を導入したからといって、まだ実際の量子理論が創られているわけではない。そこに至るまでに通過しなければならぬ研究の残った道程は、おそらくそれこそ、O・レーマーによる光速度の発見から、マクスウェルによる光の理論の基礎づけまでと、同じほどにも遠かろう。十分に保証された古典理論の中へ作用量子を導入することが、当初から出会ってきた困難については、すでに触れたとおりである。
それは、年とともに減るよりもかえって増したのであり、かりにその間に性急な研究の前進が、そのうちのいくつかをしばらくは無視したとしても、残されてあとからの補完をまっている欠陥は、誠実な体系家をそれだけいっそう苦しめるのである。
とりわけ、ボーアの理論において、作用法則を構成するための基礎となっているものは、一世代前ならどんな物理学者でも、疑いもなく直ちに拒否したであろうような、いくつかの仮説からなり立っている。原子の中では、ある完全に限定された、量子的に記述される軌道が特別の役割りを演ずる、といったことならまだしも、この軌道の中を一定の加速度で回っている電子が、全然エネルギーを放出しないということになると、とてもこれは考えうることとして受け入れられはしなかったであろう。
さらには、ある放出された光量子のはっきりと確定された周波数が、それを放出する電子の周波数とは異なるはずだということなどは、古典学派の中で育った理論家には、一見しただけで、奇怪な表象力にはほとんど耐えがたい期待であると感じられたに違いない。
しかしながら、数字が動かせぬ証拠を示した結果、今と以前とではしだいに立場が入れ替ってしまった。当初の問題は、確実なものとして一般に承認されている枠組の中に、新たな異種の要素を多少とも強制気味にあてはめることであったのに、その侵入者が一定の安全地点を略取してからというもの、今では逆に攻勢に転じて、それが古い枠組をなんらかの仕方で爆破するであろうことは、今やすでに明らかとなっている。どの点で、どの程度までそれができるかということだけが、まだ問題であるにすぎない。
もし、この激しい格闘の期待される結果を今から推測して語ることが許されるならば、古典理論の中からは熱力学の大原則が、量子論においても、その中心的な場所を不可侵と宣言するのみか、さらにはこれを適当に拡大するでもあろうことは間違いないようにみえる。
古典的熱力学の基礎づけに際して思考実験が演じた役割りを、量子論においては、P・工ーレンフェストの断熱仮説[P. Ehrenfest, Ann. d. Physik, Bd.51, p327, 1916]が当分ははたすだろうし、またR・クラウジウスが、エントロピー測定のための出発点として、物質系の任意の二つの状態は、適当に操作すれば可逆過程によって相互に移し変えられるという公理を導入したように、ボーアの新しい着想[対応原理]は、彼によって開示された不思議の国の内部に至る、まったく同様の道があることを明らかにした。
こまかく見れば、私の意見では、それに完全に解答を与えることによっていっそう進んだ解明が期待できそうな、ある特別の問題がある。放出され終ったあとの光量子のエネルギーは、いったいどうなるのかという問題である。
それは、ホイヘンスの波動理論の意味での伝播を続けるうちに、さまざまな方向へとひろがってしまい、たえずより大きな空間をしめることによって、無眼に希薄になってゆくのだろうか。それとも、ニュートンの流出理論の意味で、唯一の方向へと弾丸のように飛び続けるのだろうか。
最初の場合ならば、量子はそのエネルギーを唯一の空間点に強く凝集して、そこにある電子をその原子結合から解き放つことはもはやできないであろう。第二の場合ならば、静力学的な場と動力学的な場の連続性という、またそれとともに、きわめて明細に調べつくされた干渉の現象についての完全な理解という、マクスウェルの理論の重要な成果はなり立たなくなろう。
いずれにしてもこれは、今日の理論にとってきわめて面白くない帰結である。
ところで、いずれの場合になるにしても、科学がこの困難なディレンマをもいつかは克服して、今日われわれには不満に思われていることも、将来より高い見地からすれば、まさに特別に調和のとれた、単純なこととみなされるようになるだろうという期待については、どんな疑念も生じえないのである。
しかしながら、この目標の達成に至るまでは、作用量子の問題は、探究をたえず新たに鼓舞もし、実らせもすることをやめないだろうし、また、その解決を妨げる困難が大きければ大きいほど、結局はそれがわれわれの物理学的な認識全体の拡大と深化にとって、それだけより有意義であったこともわかるであろう。