
このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
電気回路の計算で利用するキルヒホッフの法則とは以下のようなものです。



位相幾何学にオイラーの多面体定理というものがある。
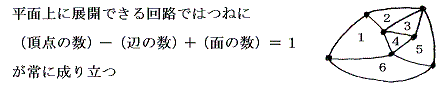
例えば上右図の例では(頂点の数)v=7、(辺の数)e=12、(面の数)f=6となり 7−12+6=1 は確かに成立している。

この定理を使えばキルヒホッフの法則の意味が明確になる。

[補足説明] 2019年4月追記
オイラーは多面体定理をもう少し一般的な形で論じています。そのとき“オイラーの特性数(標数)”が重要な意味を持ちます。そして、この位相幾何学における大定理は様々な応用があります。読者の方から教えて頂いたのですが、家政学における衣服の裁縫に応用できるとはビックリです。このことに関しては別稿「微分幾何学」3.(11)2.[補足説明]をご覧下さい。
以下の回路を流れる電流 I1〜I6 を求める問題を例にして独立なキルヒホッフの法則の数を説明する。
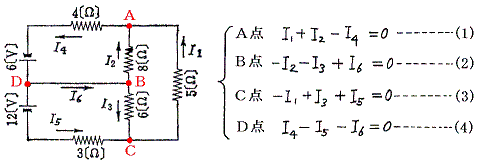
節点は4つあるので式は4つ得られるが、このうち独立なものは(節点数−1)=3個である。それは以下の理由による。各電流が流れる辺の両端が節点であるから(1)〜(4)式の中に I1〜I6 は+で1回、−で1回ずつ現れる。だから(1)〜(4)式の辺々を加えると
![]()
となり自明の式となる。故に(1)〜(4)式の内の任意の1個は残りの(節点数−1)個の式を加え合わせることにより表現することができる。ゆえに独立な第1法則の数は(節点数−1)個である。
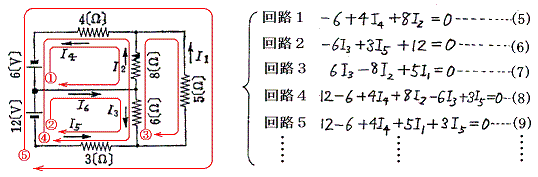
回路式は様々考えられるが独立なものは回路によって区切られる面の数と同じ3個である。それは以下の理由による。例えば回路5についての式(9)は(5)+(6)+(7)の3つの回路についての第2法則に分解できる。なぜなら各面についての回路式の電圧変化を見積もる方向をいっも時計回りの方向に定めると、回路1、2、3についての第2法則(5)(6)(7)において辺が重複する部分では+と−が逆で現れてくるので(5)〜(7)を加え合わせると重なる部分が互いに打ち消し合って(9)式になるからである。任意の回路は必ず(5)〜(7)の回路式の和で表される。故に独立な式の数は面の数に一致する。
以上の考察から明らかなように、以下の6個を連立させて解けば良い。
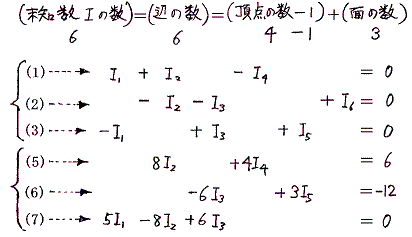
この連立方程式を解くと
![]()
が得られる。
ところで今日では、こういった連立1次方程式は、一般的に解く方法が確立しており、下記の様な行列方程式を解けば良い。
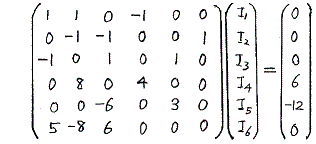
この行列方程式の解き方は、別稿「行列式と行列」1.(5)をご覧下さい。
ただし計算はかなり面倒なので、実際は電子計算機プログラムによって解きます。