�@���̃y�[�W�������������������̃o�[�W�����������p�������B�u���E�U�[�ł͌��ɂ����̂ł�������͑N���ł��B
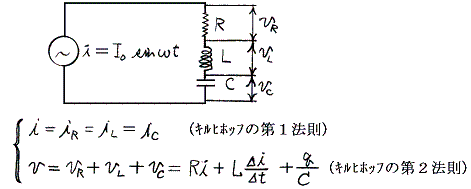
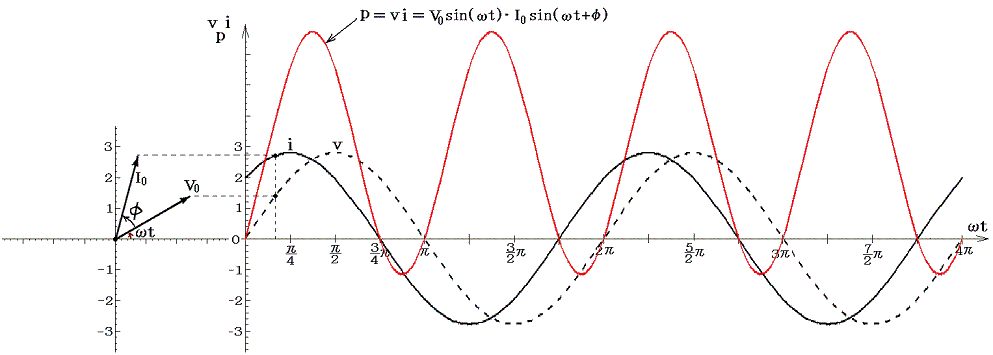
�@�d�C�H�w�̑啔���̖��͂��₩�ɕω������Ɋւ�����̂ł���B���₩�ɕω������Ƃ͐U���̈�����̊ԂɌ��肪�i�ދ������A���u�̑傫���ɔ�ׂ��ꡂ��ɑ傫���ƌ������Ƃł���B�܂��H�̂���Ƃ���ŋN�������ω��͏u���ɉ�H�S�̂ɋy�сA��H���\������e�����݂͌��ɗ͂̊W���������ē������ē����B
�@������𗬂ɂ���H�����E����������d�ׂ��A�e�u�ԏu�Ԃ�������͂͂荇���Ă���A�d�ׂɓ������͂͏�ɗ�ł���ƌ��Ȃ����B���ۂ͂����͂��̗͂̃o�����X�̕��ꂪ�d����d�ʂ�ϓ�������̂����A�e�u�Ԃ̂����̕ω����������邽�߂ɓ����d�C�ʂ́A��H�S�̂𗬂��d���̓d�C�ʂɔ�r�����疳���ł���قǏ����ł���A�܂��e�u�Ԃ̊e�����̓d�ʂ��������邽�߂̓d�ו��z�̂�蒼���ɗv���鎞�Ԃ́A�𗬂̕ϓ������ɔ�r�����疳���ł��邭�炢�ɒZ�������ɂ����Ȃ���B
�@�܂�𗬉�H�̒��ŋN�����Ă��鎖�́A�����玞�ԓI�ɕϓ����錻�ۂł��A�e�u�ԏu�Ԃɉ����Ă͗͂̒ނ荇�����������ꂽ����Ԃł���ƌ��Ȃ���B������𗬂��u���l�ɂ��āA�e��H�f�q�͔��d�@�ɓ������Ă���B���̂Ƃ��L���q�z�b�t�̖@�������̂܂ܐ��藧���A����𗘗p���Ę_���鎖���ł���B

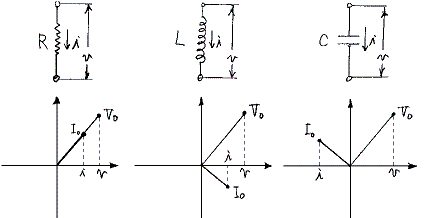
�@�e��H�f�q�ɂ́A���d�@�����������p�U�����ւ̎����I�d���������B���̂Ƃ��e��H�f�q�𗬂��d���Ƒf�q�Ɋ|����d���̊W�͕ʍe�u�𗬓d�C��H�v�Ő��������悤��
������

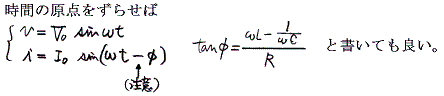
�@�e��H�f�q�͑O�q�̗l�ɔ��d�@�Əu���ɏ�������肵�āA���݂�������B���̂��߁A��H�f�q�q�A�k�A�b�ɂ́A���ׂē����p�U�����ւ������ŕ\�����d�����|����B�̂ɂ����̘a�͓����p�U�����ւ̈�̎O�p���ɓ��������B
�@���d�@���������ꂽ�`�̂��������ŋN�d�͂����Ă���Ƃ���ƁA���������Ƃ̎O�̂��������ɕ����ł���B�����������ꂼ��ɂ��āA�e�q�A�k�A�b���P�Ƃɑ��݂����Ƃ��ɐ��藧�������Ƃ��̊W�����̂܂ܐ��藧�B������e��H�f�q�ɉ��������d�͂ɂ��Ă��A���̂Ƃ��̌��_�����̂܂ܐ��藧�B
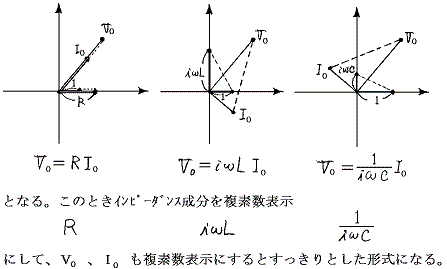
�d���Ɠd���̔��萔���C���s�[�_���X�ƌ����B�O�L���_���

�ƂȂ�B���̊W��}�������
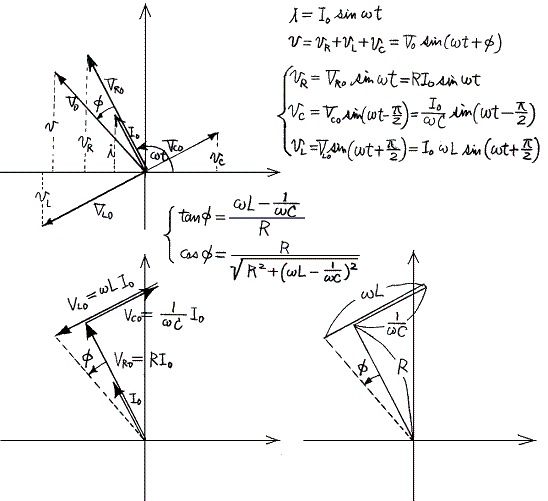
�@�ƂȂ�A���������̘a�́A��̂��������ɒu����������B����͊e��H�f�q�Ɋ|����d�����p���x�ւʼn�]����x�N�g���ŕ\���A���̃x�N�g���a���Ƃ�Ηǂ������Ӗ�����B�����āA�Ō�ɍ����x�N�g���̐������ւ̎ˉe�����������H�̗��[�Ɋ|����d���̏u���l�ł���B���̂��Ƃ��A��ŏq�ׂ����f���\���ɂ��戵�̒��z�ɔ��W����B
�d�����̏u���l���v�Z�����
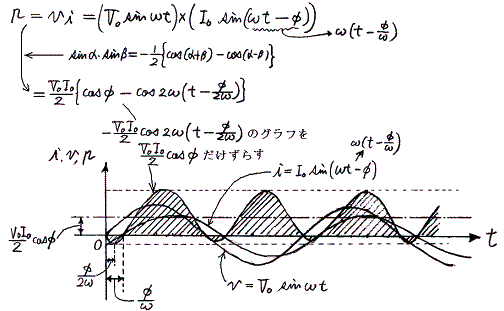

�d�����̎����l�o�͎d�����̏u���l���̎��ԓI���ς������L���̑�P���̂ݎc��

���̊W���͍ŏ��ɏq�ׂ����Ƃ����悶�Ď��ԕ��ς������̂ɁA�ʍe�u�𗬓d�C��H�v�̌��_��p���Ă����܂�B
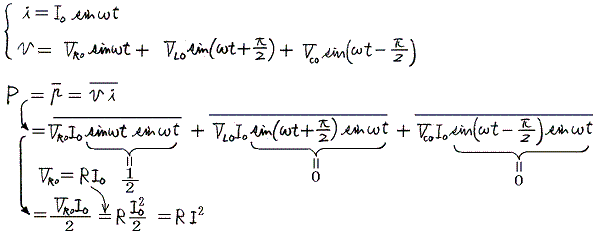
�@��H���쓮���锭�d�@�̓d���u�O�����Ƃ���ƁA��H�𗬂��d���͍����C���s�[�_���X�̒l�ɂ��ω�����̂͂������ł��邪�A����ɔ��d�@�̌𗬂̊p�U�����ւ̒l�ɂ��ω�����B
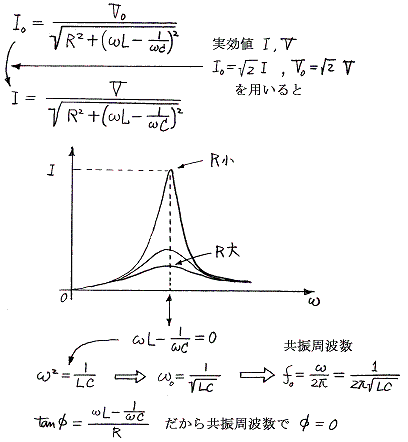
�܂�ց�1/�i�k�b�j1/2�̂Ƃ��ő�̓d���������B
�@����͂q�A�k�A�b�̒����H�̒�R�l�́A�����̊e�X�̒�R�l�i�C���s�[�_���X�j�q�A�ւk�A�i�P�^�ւb�j�̘a�ɂȂ邱�Ƃ���\�z�ł��邱�Ƃł���B�Ȃ��Ȃ�A�R�C���̒�R�͍����g�ő傫�������Ń[���i�Z���Ɠ����j�A�R���f���T�[�̒�R�͍����g�ŏ����������Ŗ�����i�f���Ɠ����j�Ȃ̂�����A���钆�Ԃ̎��g�������ց^�Q�ō�����R���ŏ��ɂȂ�ł��낤����B
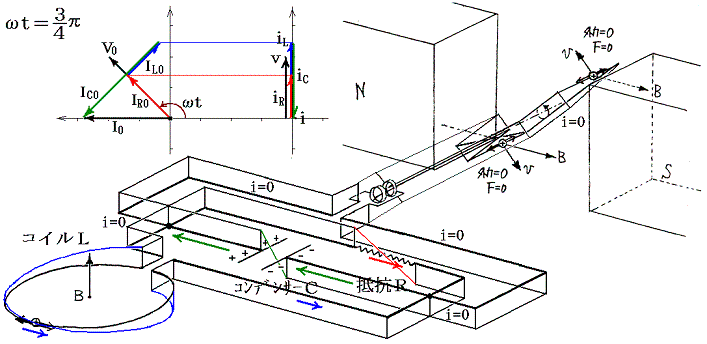
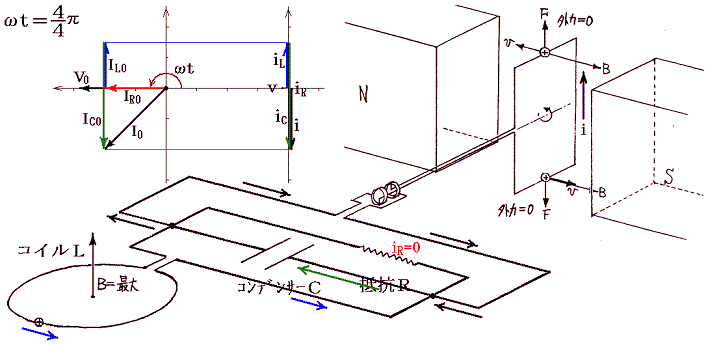
��Ƃ��Ĉȉ��̏ꍇ��}������B����₷���悤�Ɏ������𐂒��ɂ��āA���Ԃ̌��_�����炵�Ă���B
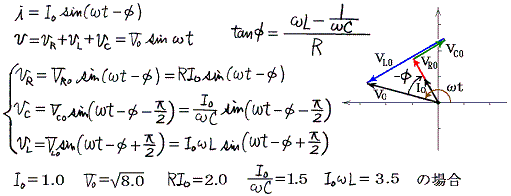
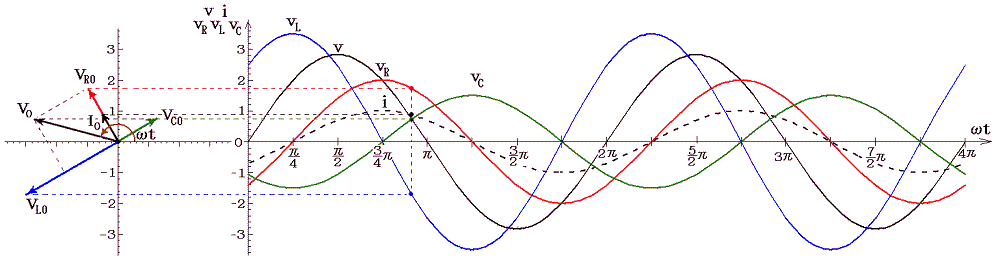
| �ւ� | 0 | (1/4)�� | (2/4)�� | (3/4)�� | (4/4)�� | (5/4)�� | (6/4)�� | (7/4)�� |
| �� | -0.71 | 0 | 0.71 | 1 | 0.71 | 0 | -0.71 | -1 |
| v | 0 | 2 | 2.83 | 2 | 0 | -2 | -2.83 | -2 |
| vR | -1.41 | 0 | 1.41 | 2 | 1.41 | 0 | -1.41 | -2 |
| vC | -1.06 | -1.5 | -1.06 | 0 | 1.06 | 1.5 | 1.06 | 0 |
| vL | 2.47 | 3.5 | 2.47 | 0 | -2.47 | -3.5 | -2.47 | 0 |
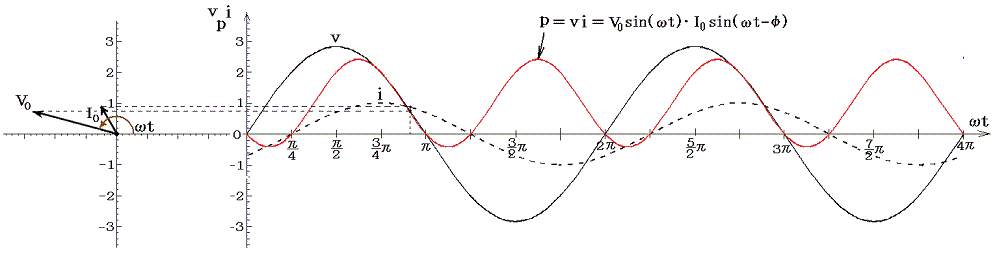
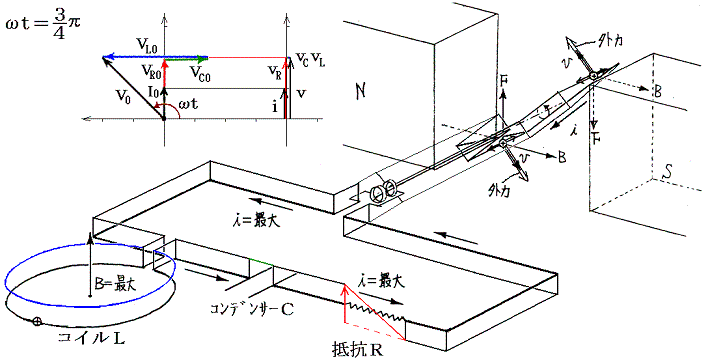
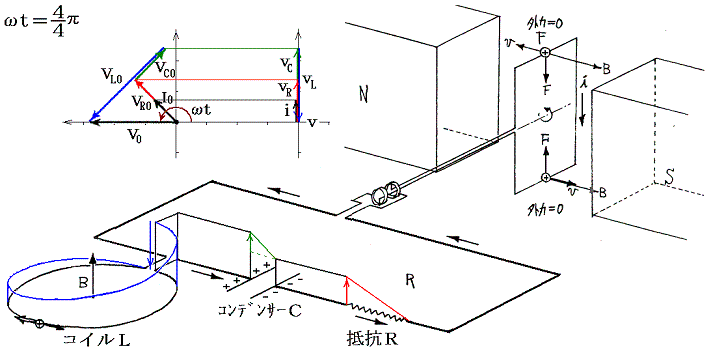
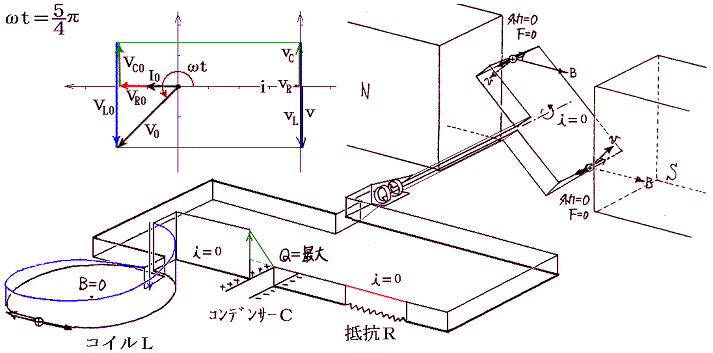
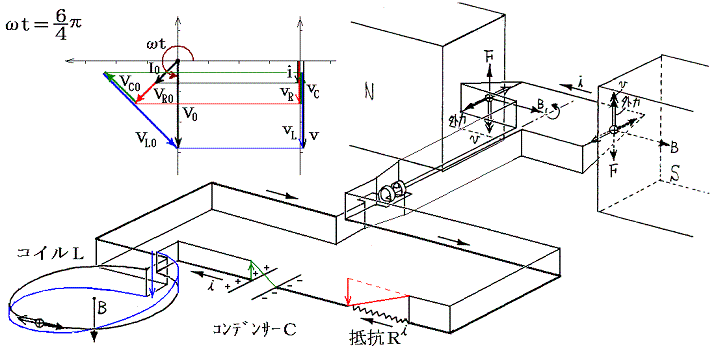
�@���d�@�R�C���𗬂��d�����R�C���ɋy�ڂ����e�ƁA����ɍR���ĉ�]�q����]�����邽�߂��O���̕����ɒ��ӁB�e���O���̉�]�����̐����́A�݂��ɋt��������ɂ荇���Ă����B
�@���}�ɂ͌���Ă��Ȃ���0���ւ����i1/4�j�A���ւ����i5�^4�j�ł��O���̕����͉�]�����Ƃ͋t�ɂȂ��Ă���A�d�����������ɂȂ�B����ȊO�̊��Ԃł��O���͉�]�����������Ă���A�O�͔͂��d�@�̉�]�q�����̎d��������B�����̎d���͈ꎞ�I�ɃR�C����R���f���T�[�̃G�l���M�[�Ƃ��Ē~����ꂽ����o���ꂽ�肷�邪�A�����̎d���̍������ŏI�I�ɒ�R�ł̃W���[���M�ƂȂ��ď�����B
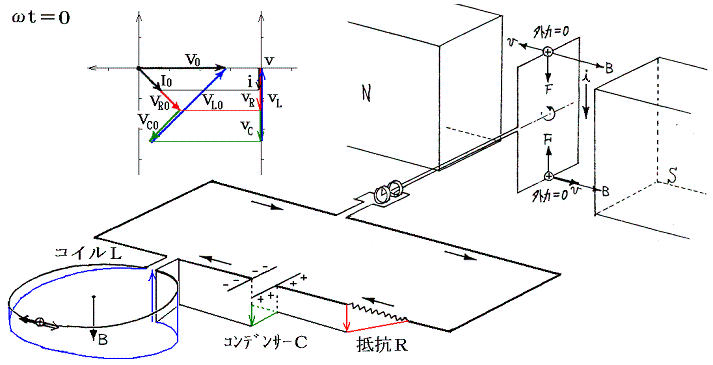
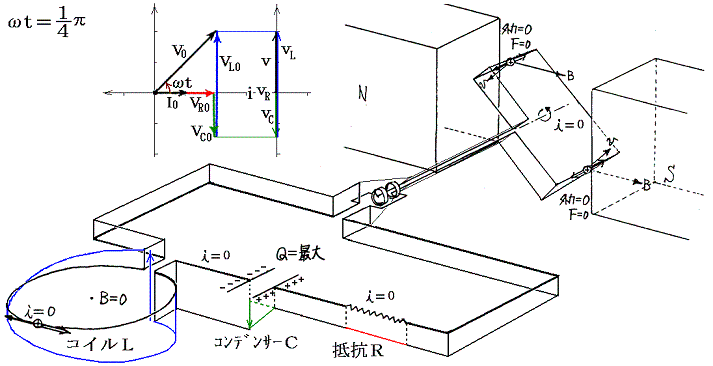
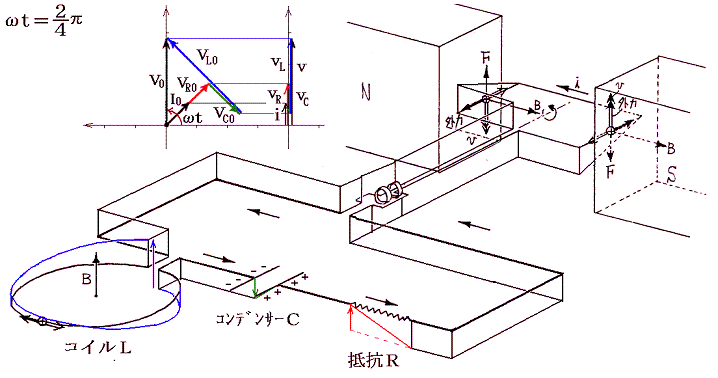
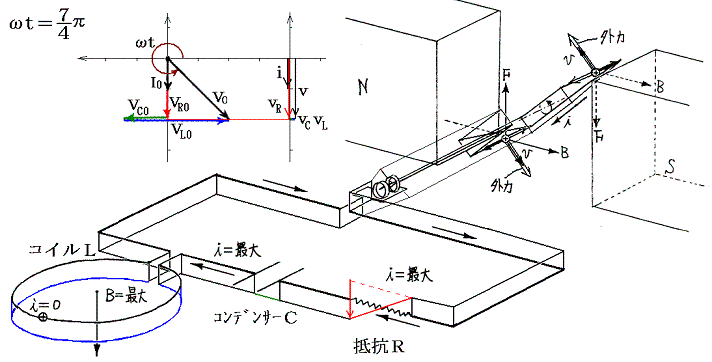
���P�D�̍ŏ��ɏq�ׂ����R�ɂ��A���̏ꍇ���𗬂��u���l�ɂ����L���q�z�b�t�̖@�������藧�B
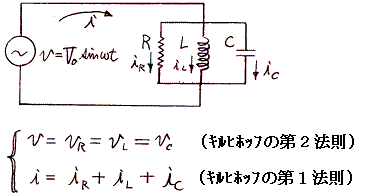
�@�e��H�f�q�̂��ׂĂɁA���d�@�����������p�U�����ւ̎����I�d�����|����B���̂Ƃ��e��H�f�q�ɂ�����d���Ƒf�q�𗬂��d���̊W�͕ʍe�u�𗬓d�C��H�v�Ő��������悤��
������

�@�e��H�f�q�͔��d�@�Əu���ɏ�������肵�āA���݂�������B���̂��߁A�e��H�f�q�ɂ͂��ׂē����p�U�����ւ������ŕ\�����d���������B�̂ɂ����̘a�͓����p�U�����ւ̈�̎O�p���ɓ��������B
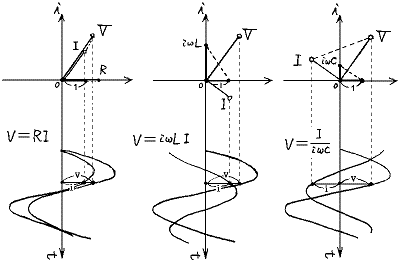
�d���Ɠd���̔��萔���C���s�[�_���X�ƌ����B�O�L�̊W���

�ƂȂ�B���̊W��}�������
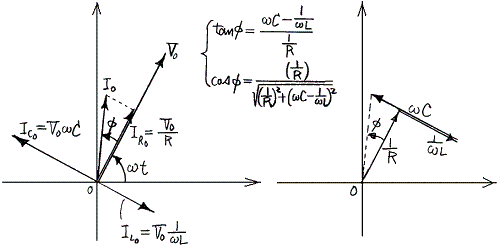
�@�ƂȂ�A���������̘a�́A��̂��������ɒu����������B����͊e��H�f�q�𗬂��d�����p���x�ւʼn�]����x�N�g���ŕ\���A���̃x�N�g���a���Ƃ�Ηǂ������Ӗ�����B�����āA�Ō�ɍ����x�N�g���̐������ւ̎ˉe�����������H�𗬂�鍇���d���̏u���l�ł���B���̂��Ƃ��A��ŏq�ׂ����f���\���ɂ��戵�̒��z�ɔ��W����B
�d�����̏u���l���v�Z�����
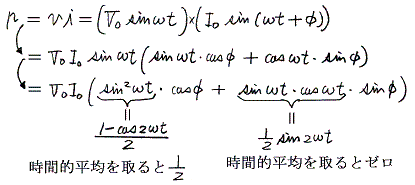
�d�����̎����l�o�͎d�����̏u���l���̎��ԓI���ς������L���̑�P���̂ݎc��
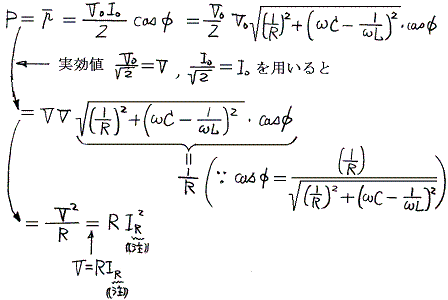
����̏ꍇ���A����̏ꍇ�Ɠ��l�ɒ�R�œd�͂�����邾���ł���B
���̊W���͍ŏ��ɏq�ׂ����Ƃ����悶�Ď��ԕ��ς������̂ɁA�ʍe�u�𗬓d�C��H�v�̌��_��p���Ă����܂�B
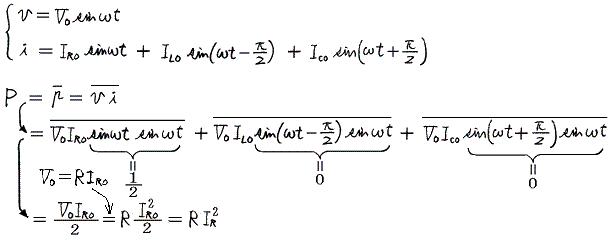
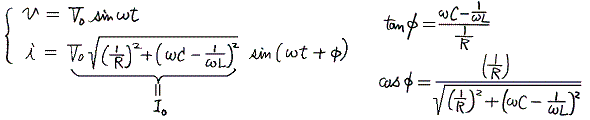
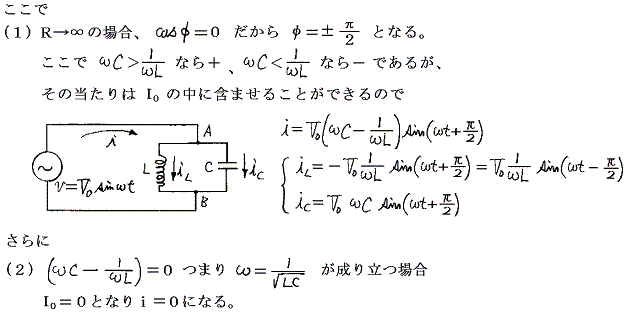
�@�i�P�j�i�Q�j�����藧�ꍇ�A�d������̓d���͗���Ȃ��ł`�_�Ƃa�_�̓d�ʂ������u0�������ւ��ŕϓ����邱�Ƃ��Ӗ�����B���̂Ƃ��@�O��������L�{��C�@���@��C���|��L�@�ƂȂ�k�Ƃb�̊Ԃɓd�������݂ɗ���ĐU������B�܂��d������ց�1/�i�k�b�j1/2�ŐU������d��������������A�����d���@�h0���O�@�ł��A�k�b��H�ɔ��ɑ傫�ȓd��������鋤�U��H�ƂȂ�B
�@���̂Ƃ��d���̒��ɔ�������d���́A�k�b��H�̉�H�f�q������Â��鎮�i�ʍe�u�𗬓d�C��H�v�S�D�T�D�Q�Ɓj�ɂ��A�k�b��H�𗬂��d���ɊW�Â������B
�@�ʍ��u�𗬓d�C��H�v�Ő��������悤�ɁA��H�f�q�R�C���̗��[�ɂ�����d���ɑ��ė����d���̈ʑ��̓^�Q�x��A��H�f�q�R���f���T�[�̗��[�ɂ�����d���ɑ��ė����d���̈ʑ��̓^�Q�i�ށB���̂Ƃ������H�̂`�a�Ԃɓ����d���������Ƃ��A��L�Ƃ�C�͈ʑ���������������ƂɂȂ�A�k�Ƃb�ɂ͏�ɋt�����̓d��������邱�ƂɂȂ�B���̂Ƃ�
�ƂȂ邪�A�P�^�ւk�ƃւb���������Ȃ����L�Ƃ�C�̐U�����������Ȃ�A��}�̕��������ŐU���ł��邱�ƂɂȂ�B���ꂪ�܂��������U�̏����ł���B
�@�����O������d������菜���Ă�����͕ω����Ȃ��B�܂�
![]()
�ŐU�����鐫���������Ă���ƌ�����B���ہA���̉�H��d�����ʂŁA�d�����a�ɂȂ钼���H�Ƃ݂Ȃ��ƃL���q�z�b�t�̑�Q�@�����
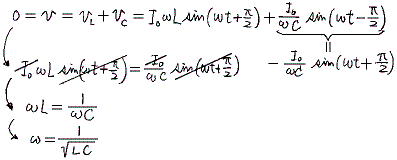
�ƂȂ�B����͍��P�D�i�S�j�̉�H
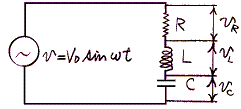
�@�łq���O�ɂ����Ƃ��̉�H�Ɠ����ł���B�܂肱�̉�H�ł��d�������p�U�����@�ց�1/�i�k�b�j1/2�@�̓d��������������A�d���d���u0���O�@�ł��A�k�Ƃb�ɑ傫�ȓd��������鋤�U��H�ƂȂ�B
�@���̂Ƃ��d���̒��𗬂��d���́A�k�b��H�̉�H�f�q������Â��鎮�i�ʍe�u�𗬓d�C��H�v�S�D�T�D�Q�Ɓj�ɂ��A��H�f�q�Ɋ|����d���ƊW�Â������B
�@�ʍ��u�𗬓d�C��H�v�Ő��������悤�ɁA��H�f�q�R�C���𗬂��d���ɑ��ė��[�ɂ�����d���̈ʑ��̓^�Q�i�݁A��H�f�q�R���f���T�[�𗬂��d���ɑ��ė��[�ɂ�����d���̈ʑ��̓^�Q�x���B���̂Ƃ������H�𗬂��d���͋��ʂ�����A���}���`���b�̂�L�Ƃb���a�̂�C�͈ʑ���������������ƂɂȂ�A�`���b�Ƃb���a�̓d���͏�ɋt�ɂȂ�B���̂Ƃ�
�ƂȂ邪�A�ւk�ƂP�^�ւb���������Ȃ����L�Ƃ�C�̐U�����������Ȃ�A��}�̕��������ŐU���ł��邱�ƂɂȂ�B���ꂪ�܂��������U�̏����ł���B
�@�i�`�j�Ɓi�a�j�͈قȂ��Ă���l�Ɍ����邪�A����͒P�Ȃ錩���̖��őS�����������ł���B
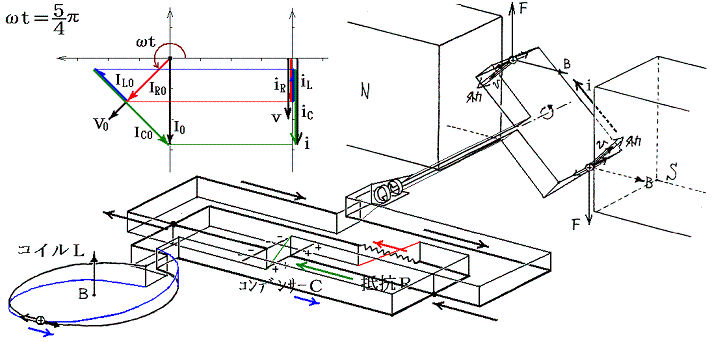
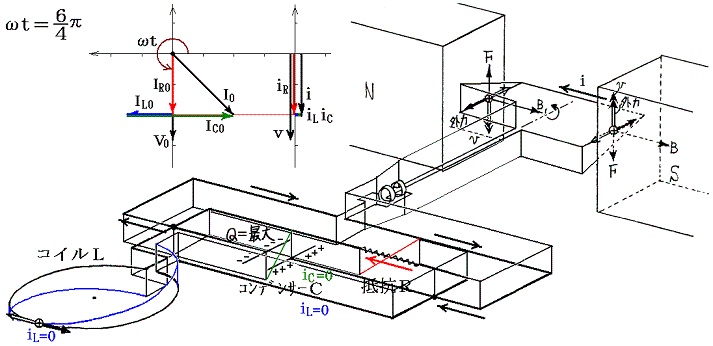
��Ƃ��Ĉȉ��̏ꍇ��}������B����₷���悤�Ɏ������𐂒��ɂ��āA���Ԃ̌��_�����炵�Ă���B
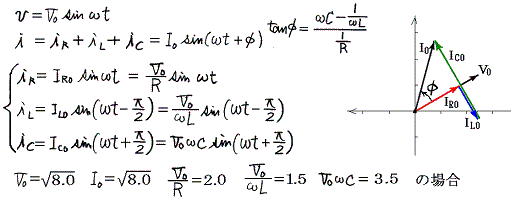
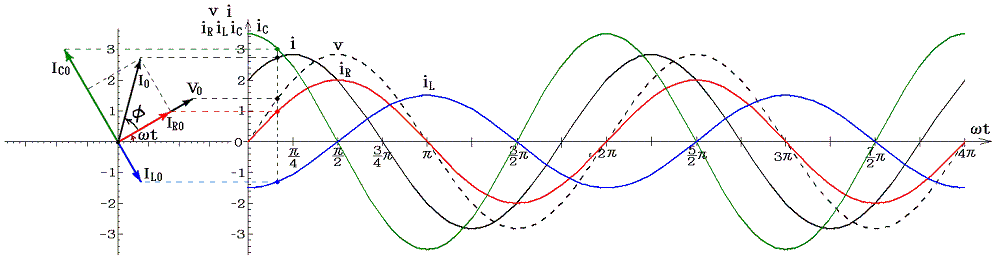
| �ւ� | 0 | (1/4)�� | (2/4)�� | (3/4)�� | (4/4)�� | (5/4)�� | (6/4)�� | (7/4)�� |
| v | 0 | 2 | 2.83 | 2 | 0 | -2 | -2.83 | -2 |
| i | 2 | 2.83 | 2 | 0 | -2 | -2.83 | -2 | 0 |
| iR | 0 | 1.41 | 2 | 1.41 | 0 | -1.41 | -2 | -1.41 |
| iL | -1.5 | -1.06 | 0 | 1.06 | 1.5 | 1.06 | 0 | -1.06 |
| iC | 3.5 | 2.47 | 0 | -2.47 | -3.5 | -2.47 | 0 | 2.47 |
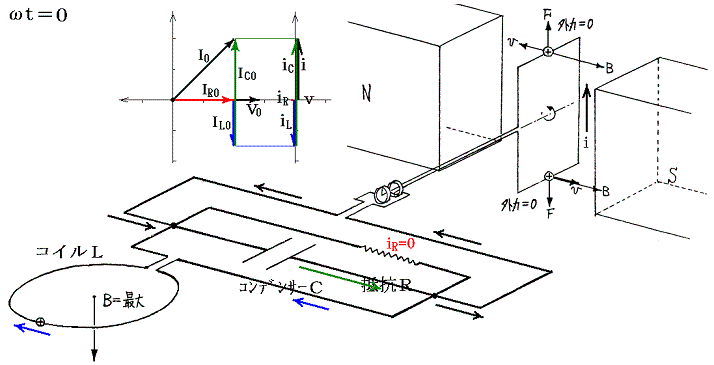
�@���d�@�R�C���𗬂��d�����R�C���ɋy�ڂ����e�ƁA����ɍR���ĉ�]�q����]�����邽�߂��O���̕����ɒ��ӁB�e���O���̉�]�����̐����́A�݂��ɋt��������ɂ荇���Ă����B
�@���}�ɂ͌���Ă��Ȃ����i3/4�j���ւ����A�i7/4�j���ւ���2�ł��O���̕����͉�]�����Ƃ͋t�ɂȂ��Ă���A�d�����������ɂȂ�B����ȊO�̊��Ԃł��O���͉�]�����������Ă���A�O�͔͂��d�@�̉�]�q�����̎d��������B�����̎d���͈ꎞ�I�ɃR�C����R���f���T�[�̃G�l���M�[�Ƃ��Ē~����ꂽ����o���ꂽ�肷�邪�A�����̎d���̍������ŏI�I�ɒ�R�ł̃W���[���M�ƂȂ��ď�����B
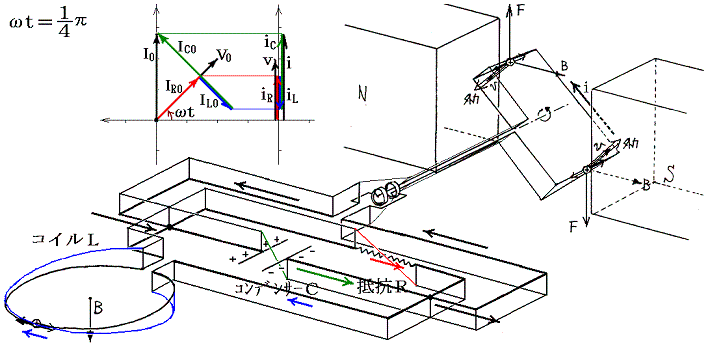
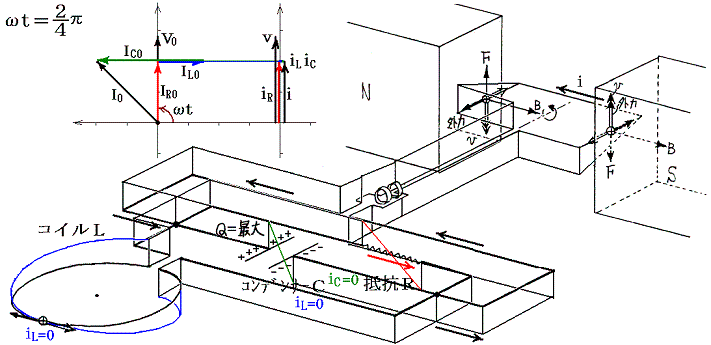
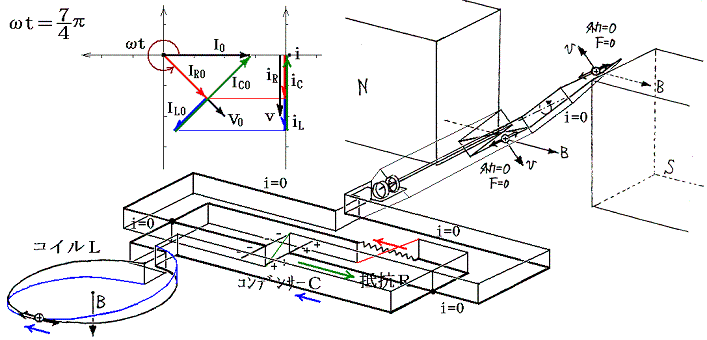
��Ƃ��Ĉȉ��̉�H���l����B�����Ō𗬓d���u�P�A�u�Q�̊p�U���������P�A���Q�ƕʁX�̒l�ł����܂�Ȃ��B
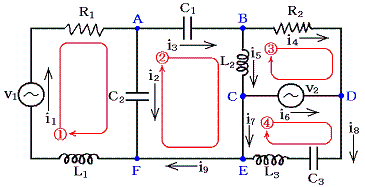
�@�����Ŏ�舵���Ă���𗬂̗l�ɁA�ꂪ���₩�ɕϓ�����ꍇ�A�e�u�ԂɊe��H�f�q�̗��[�ɐ�����d�ʍ��@���@�Ɖ�H�f�q�𗬂��d���@���@�ɂ���
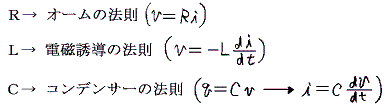
�����藧���A�܂��ɁA�����̖@�����e��H�f�q�̗��[�ɐ�����d�ʍ��Ƒf�q�𗬂��d���̊W���K�肵�Ă���B
��}�̉�H�ŁA�e��H�f�q�̗��[�̓d�ʍ���
![]()
�ŕ\���A���P�`���X�𖢒m���Ƃ��āA�L���q�z�b�t�̑�P�E��Q�@����K�p����B����͂��P�`���X�Ɋւ����萔�W���̐��`�A���Q�K��������������������ɂȂ�B���̍ۃR���f���T�[�ɍŏ��d�ׂ����܂��Ă�����ϕ��̏����l�Ƃ��čl������悢�B�����ĉ�H�Ԓ��̂��ׂĂ̎x���̓d���Ɠd�������肷�邱�Ƃ��ł���A���̉�H�Ԃ̐U�镑���̂��ׂĂ����������ɂȂ�B�������A���Ƃ����`�ł����Ă��Q�K�̘A��������������������������Z���ɂ͓���B���ꂪ�A�ȉ��̗l�ɍl��������I�ɊȒP�ɂȂ�B
��H�f�q�̗��[�ɐ�����d�ʍ��@���@�Ɖ�H�f�q�𗬂��d���@���@�ɂ��Đ��藧��
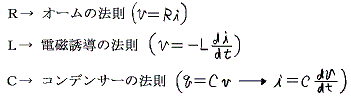
�̊W���́A����u�̕ω����p�U�����ւ̐������̏ꍇ�A���Ƃ��̊Ԃ̈ʑ��W�����}�̗l�ɂȂ邱�Ƃ������Ă���B
���̂Ƃ��A���f���̐ς̐����i���Z���w�a�ŏK���j�𗘗p�����
�@�p�U�����ւʼn�]���镡�f�x�N�g���u0�A�h0�̎������ւ̎ˉe���������ۂ̓d���A�d���̏u���l���A���ƍl����悢�B���̂Ƃ��d���̐����́A���̓d������R�ɉ�����ꂽ�Ƃ��ɓd���������������ƌ��߂Ę_����B
�@�O�L��H�Ԓ��̓d�����쓮�����d���̓d���i�d���j�����Ԃ̂������܂��͂��������ŕω����Ă���A�������𗬋쓮�d�����P�A���Q�̊p�U�����������l�ւ�����ꍇ�ɂ́A��L�i�P�j�̎戵�����I�ɊȒP�ɂȂ��B����͑O�L��H�Ԃ��𗬓d�����P�A���Q�̊p�U�����ւ����ׂē����ŁA����Ɉȉ��̂Q�_�����藧����A�������������萔�W�����A���㐔�������Œu�������邱�Ƃ��ł��邩�炾�B
�i���Ӂj�@�d�����P�A���Q�̌𗬊p�U���������P�A���Q�ƕʁX�̒l�̏ꍇ�ɂ͓��ʂȒ��ӂ��K�v�Ȃ̂Łi�S�j�Ő�������B
�@��Ƃ��đO�o�̉�H�����グ��B��������H�f�q�̃C���s�[�_���X�A�d���A�d�����ׂĕ��f���Ƃ��A�u�P�A�u2�̋쓮�p�U�����͓����l�̃ւƂ���B
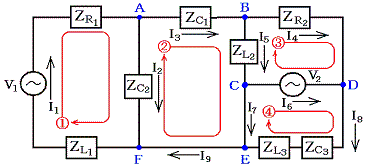
�L���q�z�b�t�̑�P�@���i����_�`�`�e�j
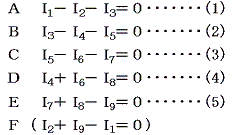
�L���q�z�b�t�̑�Q�@���i��H�@�`�C�j
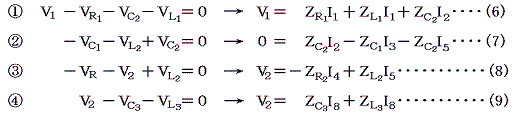
�d���Ɋւ��ẮA�d���̗��������ɉ�H��i�ނƂ��́{�ŁA�t�����ɐi�ނƂ��́|�ʼn�����B���̑��̉�H�f�q�ɂ��Ă͓d�������ɐi�ޏꍇ�|�A���̋t�ɐi�ޏꍇ�{�ł�������B
�i�P�j�`�i�X�j�����܂Ƃ߂�Ɩ��m���@�h�P�`�h�X�@�̐��`�A���㐔�������ɂȂ�B
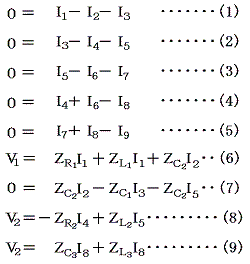
�s��\�������
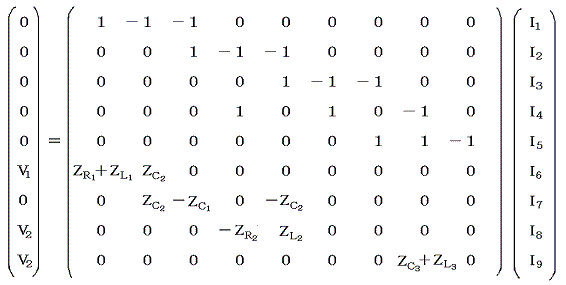
�ƂȂ�B���f���W���ł��낤�ƁA����͈�ʓI�ɉ������Ƃ��ł��āA�h�P�`�h�X�͂u�P�A�u2�̐��`�����i�퐔�W���̘a�̌`�j�ŕ\�����Ƃ��ł���B���̂Ƃ��u�P�A�u2�ɂ�����W���͈�ʂɁ@�yR1�A�yC1�A�yL1�A�E�E�E�E�E���X�̊��ł���B
�@���̂Ƃ��A���̌W���́@�yR1�A�yC1�A�yL1�A�E�E�E�E�E���X�̐ς⏤���܂ݐ��`�̊W�ł͂Ȃ����A�W���̃C���s�[�_���X�Ɋւ��Ă͏揜�Z�������Ă��Ă��ǂ��B����͂h�P�`�h�X�ɂ��Ă̓��i�u�P�A�u2�̏퐔�W���̐��`�����a�j���������ׂ��i�P�j�`�i�X�j�����ϐ��ɂ��Đ��`�ȊW������A���f���Ŗ������Ă���A���̎��������K�����̘A�������������Ă��邩��ł���B
�@������ɂ��Ă���L�A���������̕��f�������܂�B���ɂ��̋��܂������́@�yR1�A�yC1�A�yL1�A�E���E�A�Ƃu�P�A�u2��
![]()
�������Đ������A���������������悢�B���ꂪ�h�P�`�h�X�ɂ��ċ��߂���ł���B
�@�������ɂ��Ă͊p�U�������قȂ�d�����܂�ł��Ă��d�ˍ��킹�̌��������藧�B�𗬓d���u�P�A�u�Q�̊p�U���������P�A���Q�ƕʁX�̏ꍇ�ɂ͈ȉ��̎菇�߂Ηǂ��B
�@���̂Ƃ��p�U�����̈قȂ�d�����܂ސ��`��H���d�ˍ��킹�̌������K���ł���̂́A��L�̎菇�ŕʁX�ɋ��߂����ɂ����Ă̂��ł��邱�Ƃɒ��ӁB
�@���Ƃ̘A���������̒��ɈقȂ����p�U�����̕��f���\�������d�ˍ��킹�����̂����邱�Ƃ͂ł��Ȃ��B����́A���f���\����p������͖@�́A�ǂ̉�H�f�q�̓d���A�d���Ƃ������p�U�����̐����g�ł���ƌ������Ƃ�O��ɂ��Ċe�f�q�̃C���s�[�_���X�f�������Ă�������ł���B������K���e�p�U�����ɂ��ĕʌ̉�H���l���A�������ċ��߂����ɂ��ďd�ˍ��킹�������Ȃ��B
�@���܂ŏq�ׂĂ������f���\����p������͖@�����`��H�f�q�ɂ��Ă̂ݐ��藧�B���`��H�f�q�Ƃ��f�q�̗��[�Ɋ|����d���͑f�q�𗬂��d���ɔ�Ⴗ���ƌ������Ƃł���B�܂���萔���d����d���ɂ���ĕω����Ȃ��萔�̑f�q�ł���B
�@����ɑ��āA�d���ɂ��L���o�V�^���X���ς��o���N�^�ivaractor�ϗe�ʃ_�C�I�[�hvariable
capacitance diode�j��O�a�S�S�����C���_�N�^�[�Ȃǂ�����`��H�f�q�ƌĂ��B����`�ȑf�q�ɂ̓C���s�[�_���X�i�d���Ɠd���̔��萔�j���`���邱�Ƃ͂ł��Ȃ��̂ŁA�����Ő����������f���\���ɂ���͖@�͐��藧���Ȃ��B
�@���܂Ŏ��グ�Ă����d���A���W�X�^�[�A�L���p�V�^�[�A�C���_�N�^�[�ȊO�̉�H�f�q�Ƃ��āA���݃C���_�N�^�[�A�g�����W�X�^�[�A�^����Ȃǂ�����B�����̑f�q�́A���Ƃ��Ɠd���Ɠd�����P���Ȕ��W�ɂ͂Ȃ�����`��H�f�q�ł���B�����畡�f���\���ɂ���͂����H�Ɏ�荞�ނ��Ƃ͂ł��Ȃ��B�����������̉��p�ɂ����Ă͍쓮�������[�����`�ŁA�g�����W�X�^�[��^��ǂ���`�̑��u�Ƃ݂ėǂ��ꍇ������B���̏ꍇ�͓K���ȓd�����u�ɒu��������������H�ɂ��āA�O�L�̕��f���\���ʼn�͂ł����H�ɑg�ݍ��ނ��Ƃ��ł����B
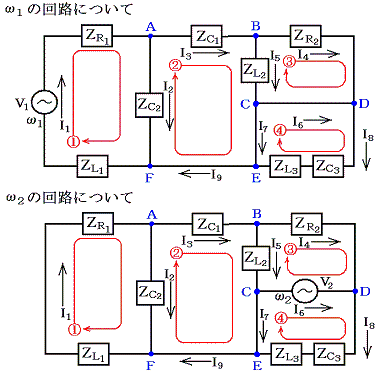
�ȉ����̂悤�ȏꍇ�̓�����H�ɂ��Đ�������B
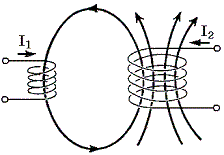
�@��}�̂悤�ɂQ�̃R�C��������A����̃R�C���̎����������̃R�C�����т��Ă���Ƃ���B���̂Ƃ��Q�̃R�C���͑��݃C���_�N�^���X�l�������A����̓d�����ω�����ƁA�����̃R�C���ɓd����������B���ݍ�p���Ă���Q�̃R�C���̋N�d�͂͂Q�̕����̘a�Ƃ���
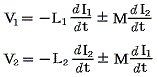
�̂悤�ɕ\�����B��Q���̕����͈���̃R�C���̎����������̃R�C�����т����@�ɊW���Đ��ɂ����ɂ��Ȃ蓾��B�e�R�C���ɔ�������N�d�͂͂Q�̕����̘a������A���}�̗l�ɂQ�̉�H���ɔ��Α��̉�H�̓d����
![]()
�ŊW�Â�����d������}������B��������Ǝ��ȃC���_�N�^���X�̌��ʂ͂��̂܂܂ŁA���݃C���_�N�^���X�̌��ʂ͗��z�I�ȓd�����Œu�������邱�Ƃ��ł���B������̓d�����̋N�d�͉͂�H�̕ʂ̕����̓d���ɊW���Ă��邪�A�����������`�ł������A��H�������Ɉ�̐��`���������t������邾���Ȃ̂ŁA�O�q�̕��f���\���ɂ���͂��ł���B
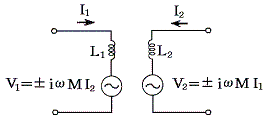
�@���͓d���Əo�͓d�������W�ɂ���͈͓��ł́A���u�̂��镔���̓d����d�����A���u�̑��̕����̓d����d���ŕ\�����Ƃ��ł��A���̂悤�ȓd������}�����邱�ƂŐ��`�f�q����Ȃ���`��H�ɕϊ��ł���B�Ⴆ�ΎO�Ɋǂ̃v���[�g��H�́A��R�ƒ���ɂȂ������d�����ŕ\����A�d���d���̓O���b�h�d���u���ɔ�Ⴗ��Ƃ���悢�B������H�͉��}�̗l�ɂȂ�B
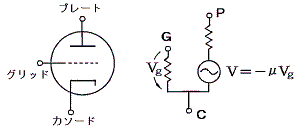
�@�g�����W�X�^�[�̃R���N�^��H�͒�R�Ƃ���ɒ���ȗ��z�I�d�����Œu�������邱�Ƃ��ł���B���̓d���̓d���̓g�����W�X�^�[�̃G�~�b�^����x�[�X�֗����d���h���ɔ�Ⴗ��B������H�͉��}�̂悤�ɂȂ�B���̂悤�ɕϊ�����ΐ��`��H�Ԃ̒��Ƀg�����W�X�^�[�̓�������荞�ނ��Ƃ��ł���B
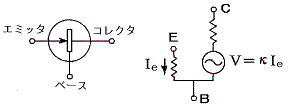
�@�^��ǂ�g�����W�X�^�[���܂މ�H�̉������߂Ă݂�ƁA�C���s�[�_���X�������������ɂȂ�ꍇ��������B�C���s�[�_���X�̎������̓G�l���M�[�������Ӗ��������A���ɂȂ�ƌ������Ƃ́A��H���G�l���M�[��������������Ƃ��Ӗ�����B�������G�l���M�[���N���ďo��킯�ł͂Ȃ��āA�d���̂c�b��H����G�l���M�[�����Ă`�b��H�̃G�l���M�[�ɕϊ������킯�ł���B�^��ǂ�g�����W�X�^�[��p���邱�Ƃɂ��A���̒�R������H���\�ɂȂ邪�A���ꂱ����������┭�U��̃��J�j�Y���ł���B