正しい振動子エントロピー表現式を用いた全エントロピー増大の証明
(「プランクの熱輻射法則」の付録2)
(1)導入
プランクは1899年5月の論文
M. Planck,“Ueber irreversible Strahlungsvorga¨nge”, Sitzunsber. Berl. Akad.
Wiss. vom 18. 5. 1899年;
[Annalen der Physik,
vol.306, (4).1, p69〜122, 1900年 に再録]
で、天下り的に仮定した振動子エントロピー表現式
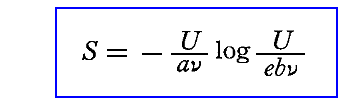
を用いて、任意の初期状態にある振動子と輻射場からなる系の全エントロピーが時間と共に増大して極大値に近づくことを証明しています。
しかし、このエントロピー表現式は正しくないことが後に解ります。プランクは1900年の12月に、真に正しい振動子エントロピー表現式
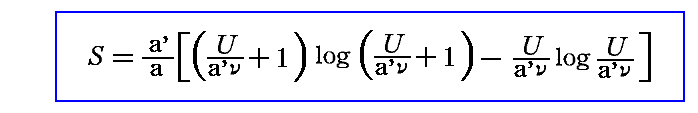
を発見します。
そのため、後の1901年の論文
M. Planck, “Ueber irreversible Strahlungsvorga¨nge (Nachtrag)「非可逆的輻射過程について(補足)」”, Annalen der Physik,
vol.311, (4)6, p818〜831, 1901年
で、振動子と輻射場からなる系の全エントロピーが、輻射の振動子による散乱過程の結果として常に増大して極大値に近づくことを、この真に正しい振動子エントロピー表現式を用いて証明し直しています。系の全エントロピーが極大を取ったときの輻射場の状態こそが黒体輻射の分布公式を与えるものだったのですからとても重要な証明です。。
この証明は、プランクの著書
マックス・プランク著「熱輻射論」(物理科学の古典7)東海大学出版会(初版の翻訳本)
Vorlesungen u¨ber die
Theorie der Wa¨rmestrahlung, Leipzig, Johann Ambrosius Barth,(初版は1906年刊)
の§187にも採録されていますので、これに従ってその証明内容を紹介します。以下の「本文」とは別稿「プランクの熱輻射法則(1900年)」の事です。「本文」4.(5)1.を参照されながらお読み下さい。
(2)系のエントロピー
1.振動子のエントロピー
「本文」8.(3)で説明したように1900年にプランクは1個の振動子のエントロピーの表現式として真に正しい形を発見します。それは

の形をしています。
2.輻射のエントロピー
上式に、「本文」3.(1)3.で証明した、1個の振動子のエネルギーUと偏光した単色輻射の輻射強度Rνの関係式、及び
、「本文」4.(3)2.で説明した、1個の振動子のエントロピーSと偏光した単色輻射のエントロピー比強度Lνの関係式を適用すると
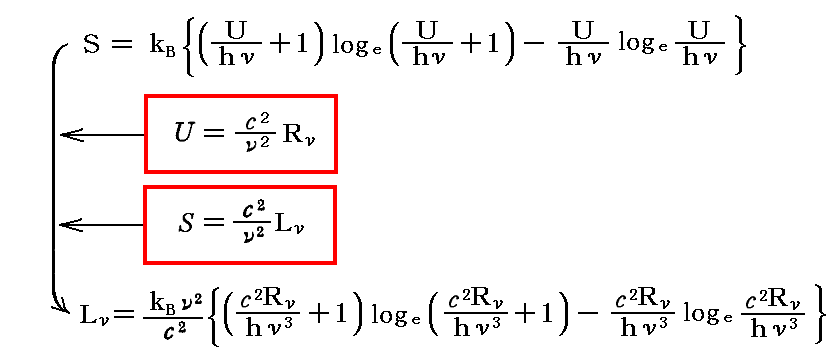
となる。
これは、別稿「ウィーンの変位則」6.(5)3.で導いた変位則の輻射エントロピーの比強度による表現
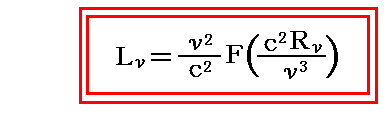
における、関数Fの具体的な形を与えるものです。
同様に、「本文」3.(1)3.で証明した、1個の振動子のエネルギーUと単色輻射のエネルギー密度uνの関係式、及び
、「本文」4.(3)2.で説明した、1個の振動子のエントロピーSと単色輻射のエントロピー密度sνの関係式を適用すると
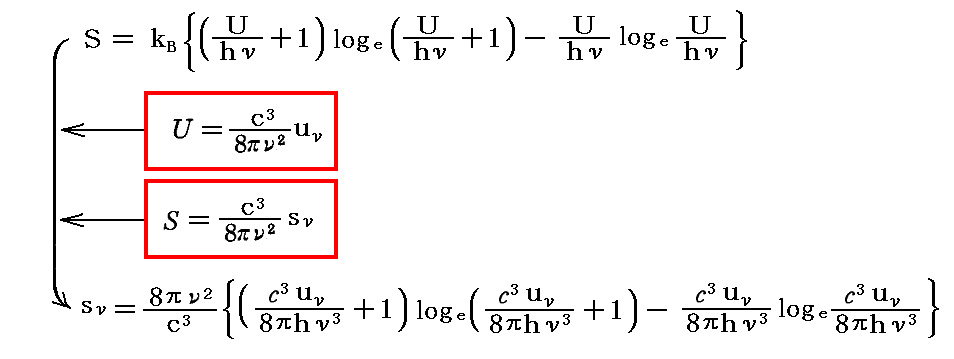
となる。
これは、別稿「ウィーンの変位則」6.(3)で導いた変位則の輻射エントロピー密度による表現
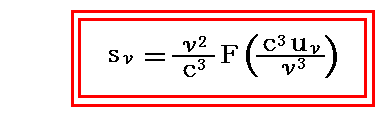
における、関数Fの具体的な形を与えるものです。
3.系全体のエントロピー
「本文」4.(2)1.で説明したように系全体としてのエントロピーStは
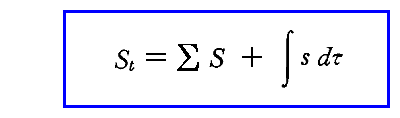
と表される。
ここでSは個々の振動子のエントロピーであり、和Σは系内の全振動子(当然、様々な固有振動数を持つものすべて)について行う。またsは輻射場の一点におけるエントロピー密度であり、積分dτは輻射が満たされている空間すべてにわたって行われる。
固有振動数νの1個の振動子のエントロピーSは
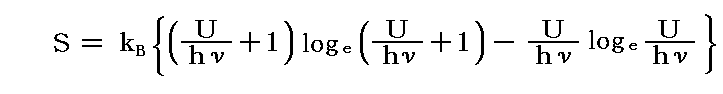
によってUの関数として与えられる。
一方、輻射場の一点に於ける輻射エントロピー密度sは「本文」4.(1)1.で説明した偏光していない輻射エントロピー比強度Mを全立体角にわたって積分することで与えられる。エントロピー輻射の主比強度をLνとLν’とすると
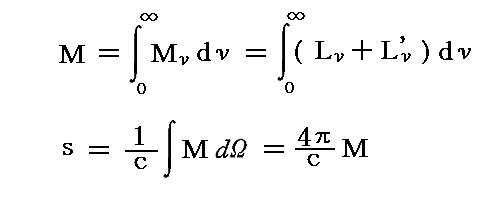
となります。
このとき、偏光したエントロピー輻射の主比強度LνとLν’は前節の式
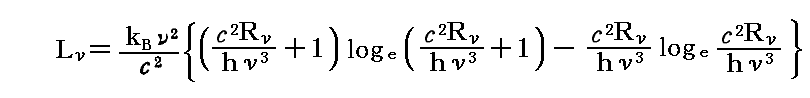
によって、輻射の主強度RνとRν’に結びつけられる。
(3)エントロピーの変化
1.輻射エントロピーの変化
もし、系内に振動子がまったく存在しなかったら、輻射線ビームはその強度を変えずに直進する。またその場合エントロピーの比強度も変化しない。完全に反射する境界面で反射が起こっても同様である。そのため輻射のエントロピーの変化は起こらない。
輻射のエントロピー変化は輻射が振動子に当たり吸収されたり、振動子から放射される電磁波が輻射に付け加わる事が起こるときに生じる。その変化を計算するには、振動子の固有振動数νに対応する単色輻射線のみを考慮すればよい。それ以外の輻射線は振動子によって影響を受けないからである。そのため以下の議論ではLに付けるべき添え字νを省略するが、Lνの意味であることを忘れないで下さい。
「本文」3.(3)で説明したように、振動子が(θ,φ)の方向に進む要素円錐dΩ内の何らかの偏光状態を持つ輻射線束によって照射されたとする。その輻射はエネルギーの強さの主値RとR’をもつ。それに対応するエントロピー輻射は、前々節(1)の関係式で結ばれる比強度(L+L’)を持つことになる。
そのため、この輻射線ビームは「本文」3.(4)2.で得られた関係式の(R+R’)を(L+L’)に変換した
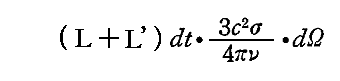
だけのエントロピーをdt時間に振動子に与える。それにより、輻射線が入射した側で同量のエントロピーが輻射場から奪い取られる。
同じく「本文」3.(3)で説明したように、他方の側で振動子から同じ(θ,φ)方向に、一定の仕方で偏光し主強度R''およびR'''の和によって与えられる強度をもつ輻射線ビームが振動子から出ていく。したがってそのエントロピー輻射は対応する比強度L''+L'''を持つ。
そのため、この輻射線ビームは「本文」3.(4)2.で得られた関係式の(R''+R''')を(L''+L''')に変換した輻射エントロピー比強度をもつ輻射線ビームが振動子から出ていく。つまり
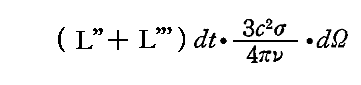
だけのエントロピーが時間dt内に周囲の場に供給される。
したがって、全体として、振動子を取り囲んでいる場の時間dt内に生じるエントロピー変化は、すぐ上の式からその上の式を引き、dΩについて積分することにより得られる。すなわち
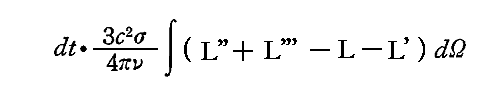
となる。
2.振動子のエントロピー変化
同じdt時間内に生じる振動子のエントロピー変化は
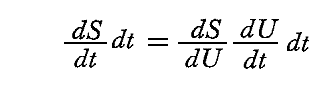
と表される。
3.系の全エントロピーの変化
系の全エントロピー変化は、前記の振動子、及び輻射に生じる変化を全振動子について和を取ることによって得られる。そのとき、「本文」3.(4)4.で導いた“エネルギー保存則”を用いると
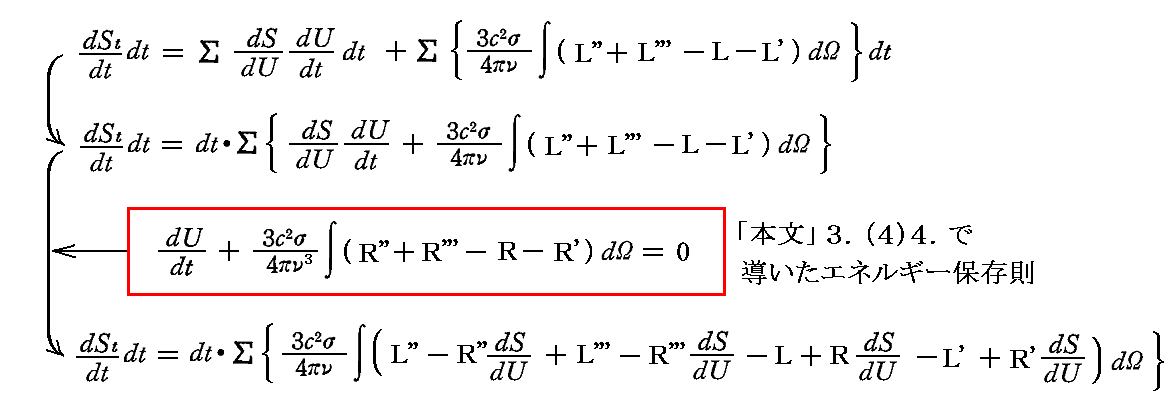
が得られる。
ここで、系内に存在する個々の振動子のまわりの輻射場に生じるエントロピー変化の全空間にわたるdτに関する積分は、全振動子について足しあわせた和Σに置き換えることができる。
また、振動数を表す添え字νはΣについて和をとる各振動子と輻射場の振動数だから、和Σを取るときに考慮されているとして、以後の展開では省略する。
(4)全エントロピーの時間的変化
ここで、系の全エントロピーStは時間と共に必ず増大するか、一定であるかのいずれかであることを証明しよう。そのためには
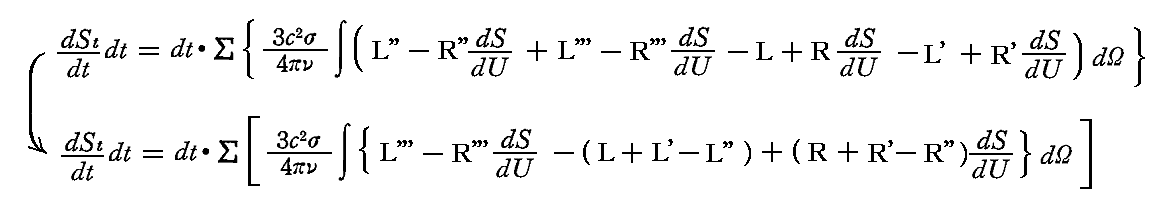
のΣ記号中の[ ]内の表式が、極限の場合のゼロを含めて常に正であることが証明できればよい。
そのためには、さらに積分記号内の{ }内表式が、正の量U、R'、R''、θ、ωの任意の値に対して正であることを証明すればよい。
このとき、「本文」3.(3)で示したように
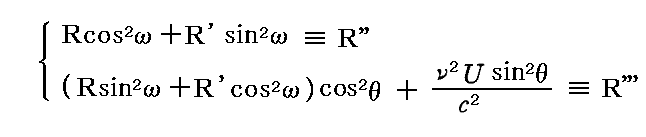
であるから、正の量U、R'、R''、θ、ωの任意の値に対して、R''もR'''も正の値になる。
さらに簡単の為に、正の量R0'''を
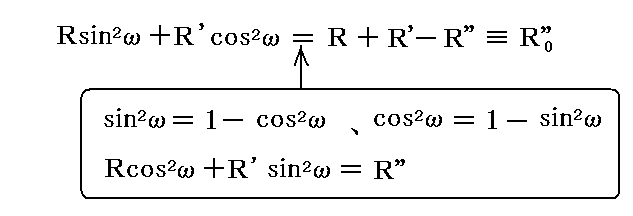
によって定める。これによって
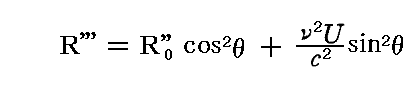
となるが、この関数のグラフは
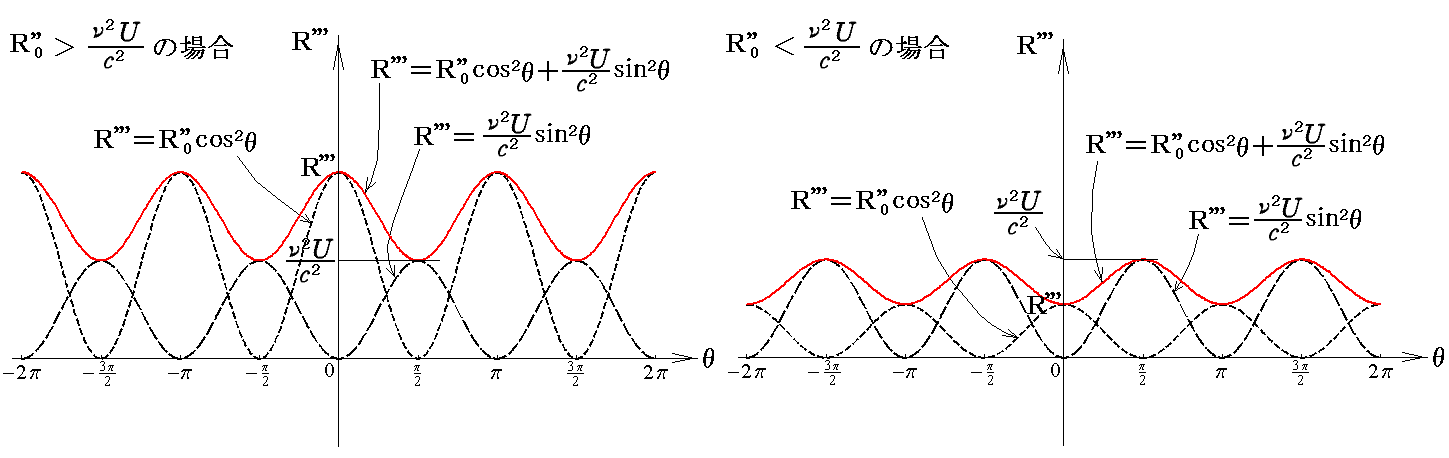
となる。このグラフから明らかなようにR'''は必ずR0'''と(ν2U/c2)の間にあることが言える。
ここで、Uが一定、したがってdU/dSが一定の場合を考える。そして
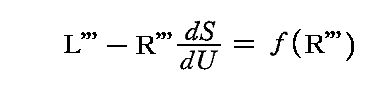
なる関数f(R''')を考える。このとき f はR'''、したがってL'''の関数である。
このf(R''')のR'''に関する一次導関数と二次導関数は
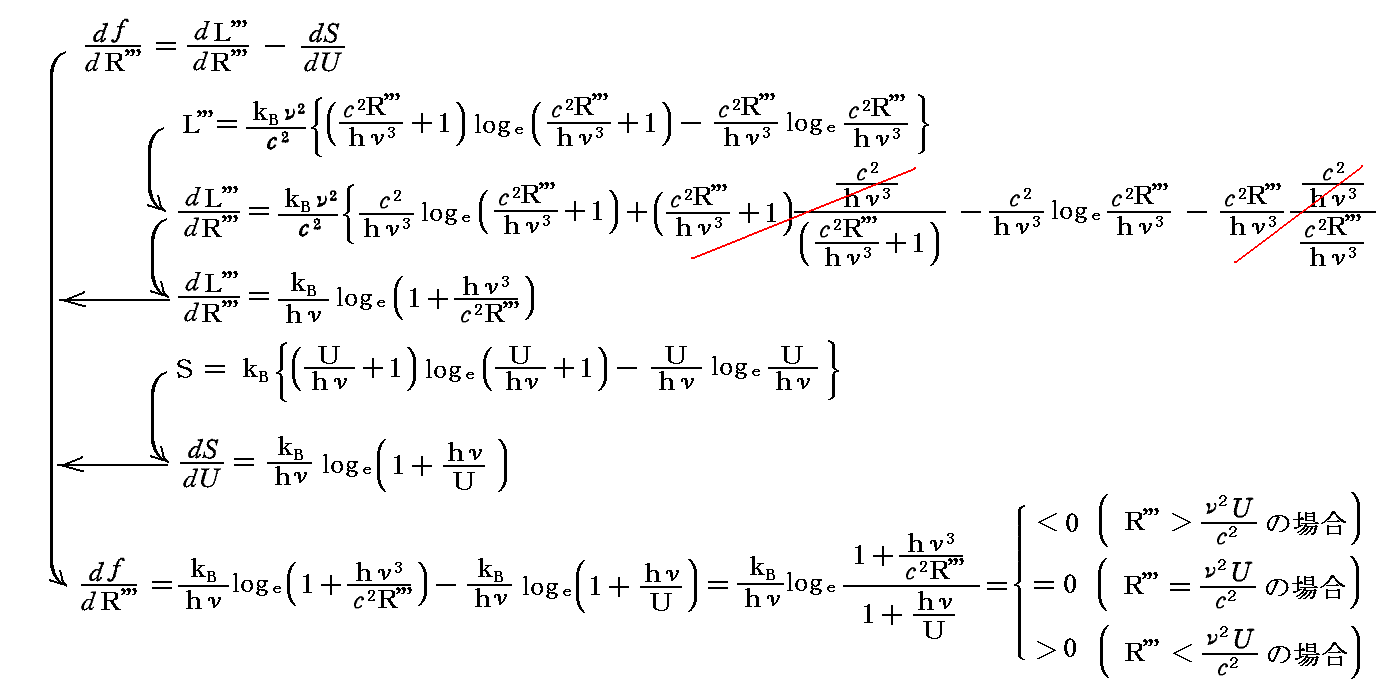
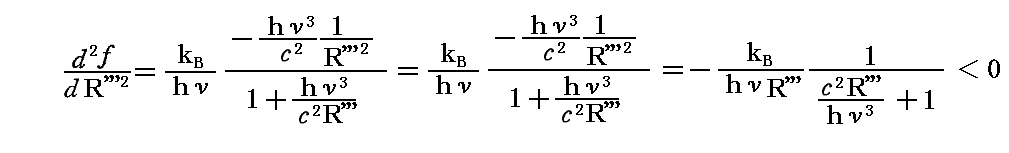
となる。そのためf(R''')はR'''=(ν2U/c2)で極大値を取る。
ところで、すでに求めたようにR'''は、R0'''<(ν2U/c2)またはと(ν2U/c2)<R0'''の大小関係にかかわらず、必ずR0'''と(ν2U/c2)の間にあるので、常に
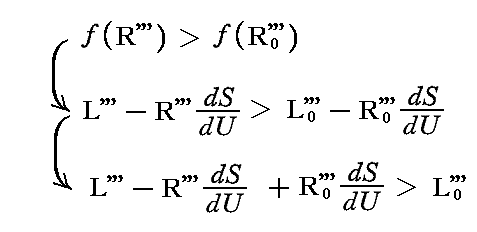
が言える。ここでL0'''はR0'''に対応するエントロピー比強度である。
この関係式を最初の積分記号内の{ }内表式に適用すると
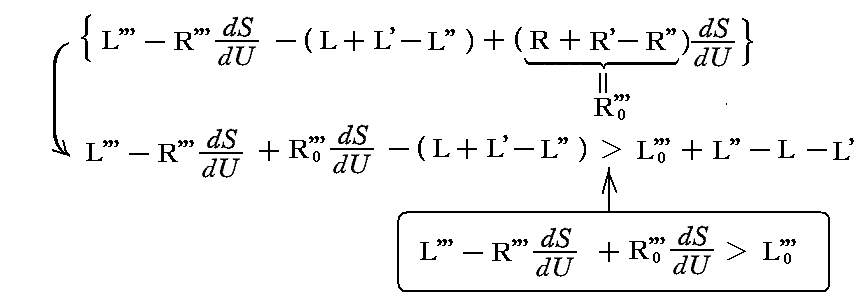
となるので、結局、L0'''+L''−L−L'>0を証明すればよいことになる。
ここでR''とR0'''についてであるが、それらは
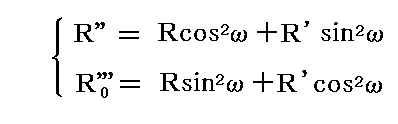
と表されるのでR'''で考察したのと同様なグラフを描いてみれば直ちに次のことが明らかになる。すなわち、R''もR0'''は、RとR'の大小関係にかかわらず、必ずRとR'の間に存在する。
ここでさらに

と置き、H=一定とみなす。つまりR'をRに、あるいはR0'''をR''に依存するとみなす。そして
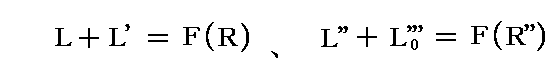
なる関数F(R)を考える。
このF(R)のRに関する一次導関数と二次導関数は
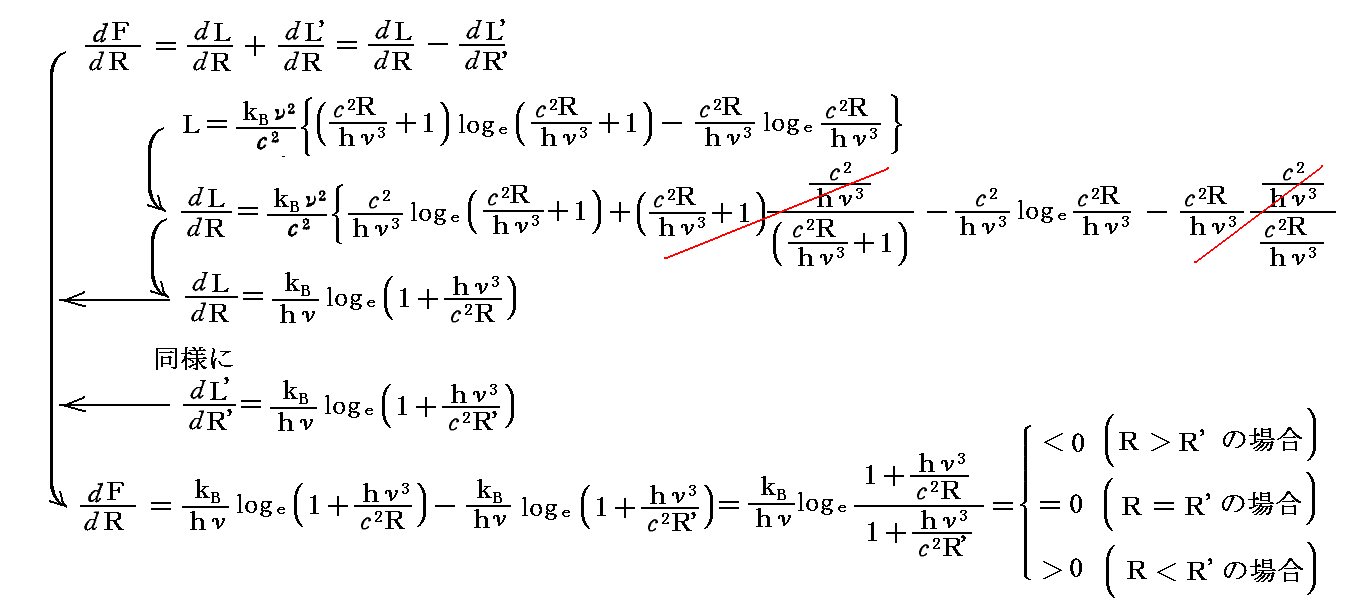
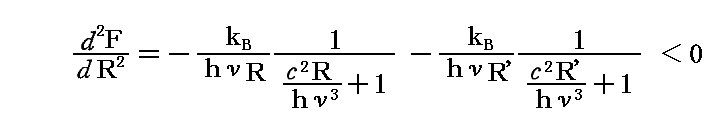
となる。そのためF(R)はR=R'=H/2で最大値を取り、その最大値の両側で対象的に減少することが解る。それゆえ変数Rの値がH/2に近づけば近づくほど、それがどちら側からであっても、F(R)の値は大きくなる。
ところで、すでに証明したようにR''もR0'''も、RとR'の大小関係にかかわらず、必ずRとR'の間に存在する。そのためR''は、RとR'の算術平均でもありR''とR0'''の算術平均でもある、H/2という値に対してRよりも近くにある。それ故に
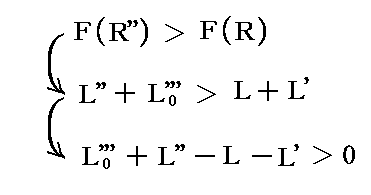
が言える。故に、系の全エントロピーが常に増大すること
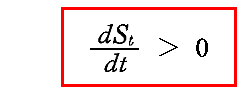
が証明できたことになる。
(5)定常的な状態
全エントロピーの絶対的な極大に対応する系の状態は、定常的な状態と呼ばれる。定常的な状態に対する必要条件は全エントロピーStが時間と共に変化しない事、すなわち前節の不等式を等式に変える条件です。それは、前節の証明から解るように、すべての位置すべての方向について
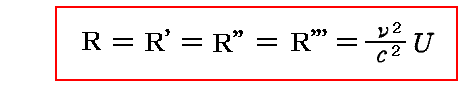
が満たされることに他ならない。つまり輻射場全体において、それぞれの振動数のすべての輻射線が偏光しておらず、等しい強さを持つことです。