このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
電流計と電圧計の利用に関しては注意すべきことが幾つかあります。
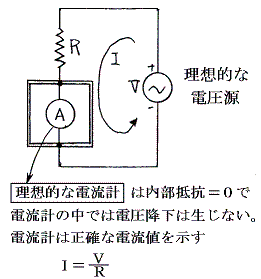
理想的な電流計とは、それを回路に挿入しても流れる電流値に影響しないものである。また下図の理想的な電圧源とは負荷が変化しても一定の電圧を保持して電流を流し続けてくれるようなものである。

電流計が理想的な場合、電流計内部では電圧降下は起こらないので、抵抗Rと、そのRを流れる電流値I(電流計の測定値)と電圧源の電圧値Vとの間にはV=RIが成り立ちVとIの測定値から抵抗値Rを測ることができる。テスターに付属している抵抗測定用のメーターは、この原理を利用して測定している。電圧源としてテスター内蔵の電池を用い、電流計の振れ幅を抵抗値に読み替えている。
しかし実際には内部抵抗が零の電流計など存在しないので、回路素子の抵抗値の厳密な測定には向かない。厳密な測定には、様々なブリッジ回路が利用され計測器内を流れる電流値が零になるような平衡関係を実現して測定される。
現実の電流計は内部抵抗がある。そのため現実の電流計は[理想的な電流計]と[小さな抵抗値r]が直列につながれているもの(下左図参照)で代用して論じられる。そして理想的な電流計が示す測定値を現実の電流計の測定値とするのだが、ここで実際に流れる電流値が電流計を挿入することにより、変化してしまうため測定値に誤差が生じる。
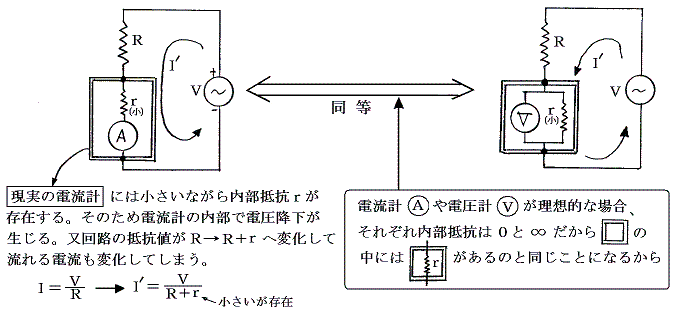
上右図に示すように、現実の電流計は[理想的な電圧計]と[内部抵抗値r]の並列結合に置き換えることもできる。ただし後で述べるように理想的な電圧計を簡便な機構で作るのは難しい。
一つの電流計で広範囲の電流値を測定するためには分流器を設置すればよい。分流器とは電流計に並列に結合する小さな抵抗rsのことである。
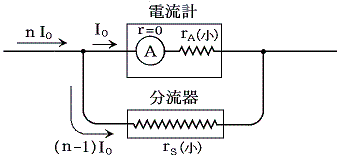
電流計に流すことのできる最大電流をI0とする。そのとき、そのn倍の電流を測定するには電流計に並列に抵抗rSの分流器を設置し、そちらに(n−1)I0の電流を逃がしてやればよい。並列回路では各枝を流れる電流値は抵抗値の逆数に比例するので I0:(n−1)I0=(1/rA):(1/rS) より rS=rA/(n−1) とすればよい。
電流の測定レンジが切り替えられる電流計の内部は下図の様になっており、使用するときは測定電流の大きさにより、接続端子(下図では−極)を切り替えておこなう。
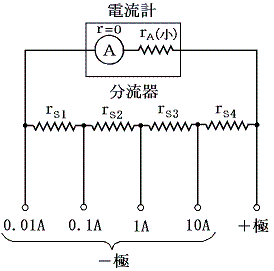
今電流計の最大許容電流が I0=0.001A=1mmAであるとする。そのとき各端子を利用した場合の測定最大電流が標記の値になるためには分流器の各抵抗値がいくらにならねばならないか計算してみよう。
10A端子を利用する場合、rA→rs1→rs2→rs3を流れる電流が最大値1mmAの場合残り9999mmAをrs4に流さねばならない。そのとき並列回路の電流値は各枝の抵抗値の逆数に比例するので 1mmA:9999mmA= 1/(rA+rs1+rs2+rs3) : 1/rs4 が成り立つ。
同様に1A端子を利用する場合、rA→rs1→rs2を流れる電流が1mmAの場合、残り999mmAをrs4→rs3 に流さねばならない。それにゆえに 1mmA:999mmA= 1/(rA+rs1+rs2) : 1/(rs3+rs4) が成り立つ。
同様に0.1A端子を利用する場合、rA→rs1を流れる電流が1mmAの場合、残り99mmAをrs4→rs3→rs2 に流さねばならない。それにゆえに 1mmA:99mmA= 1/(rA+rs1) : 1/(rs2+rs3+rs4) が成り立つ。
同様に0.01A端子を利用する場合、rAを流れる電流が1mmAの場合、残り9mmAをrs4→rs3→rs2→rs1 に流さねばならない。それにゆえに 1mmA:999mmA= 1/rA : 1/(rs1+rs2+rs3+rs4) が成り立つ。
上記4つの条件式を整理すると以下の連立方程式になる。
−rs1 −rs2 −rs3+9999rs4=rA ・・・・・・(1)
−rs1 −rs2+999rs3 +999rs4=rA ・・・・・・(2)
−rs1+99rs2 +99rs3 +99rs4=rA ・・・・・・(3)
9rs1 +9rs2 +9rs3 +9rs4=rA ・・・・・・(4)
未知数5個(rA、rs1、rs2、rs3、rs4)に対して式は4個だから未知数間の比が求まる。連立方程式の解として
rA:rs1:rs2:rs3:rs4=1:(1/10):(1/100):(1/1000):(1/9000)
が得られる。つまり、全体としての抵抗値ができるだけ小さくなるよう心がけて、その間の比がこの値になるようにする。
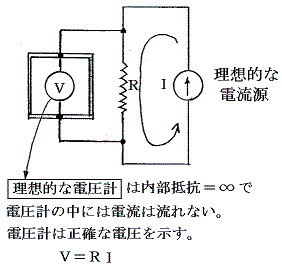
理想的な電圧計とは、それを回路に挿入しても電圧測定すべき回路素子の両端の電位差に影響が出ないものである。また下図の理想的な電流源とは負荷が変化しても一定の電流値を保持して電流を流し続けてくれるようなものである。
現実の電圧計は電流を使って針を振らせるために内部抵抗が有限で、ごく僅かではあるがその内部を電流が流れる。そのため現実の電流計は[理想的な電圧計]に[大きな抵抗r’]が並列につながれているもの(下左図参照)で代用して論じられる。
現実の電圧計が示す抵抗Rの両端の電位差V’は、測定すべき抵抗Rと現実の電圧計の内部抵抗r’の並列回路の両端の電圧を測ったものになる。そのため電圧計を接続することにより、回路素子Rの両端にかかる電圧は影響を受けて変化してしまい誤差を生じる。
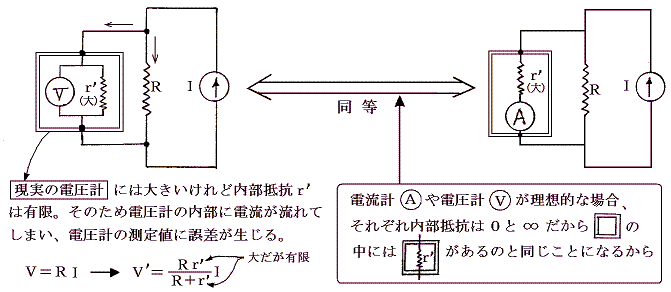
現実の電圧計にはごく僅かといえども電流が流れるので、上右図のように[理想的な電流計]に[大きな抵抗r’]が直列につながれているもので置き換えることができる。実際の電圧計はこのように電流計を用いて構築されている。別項「オームの法則」の電流値の測定で説明したように、電流値こそ電流の磁気作用(アンペールの法則)を用いて手軽にかつ正確に測ることができる量である。電圧を直接的に正確に測定する簡便な方法は無い。
一つの電圧計で広範囲の電圧値を測定するためには倍率器を設置すればよい。倍率器とは電圧計に直列に結合する大きな抵抗rMのことである。
ここで実際には、電圧計は前項で述べたように電流計と大きな抵抗値rVの直列結合で代用する。そのとき rV は R より遙かに大きな値であるから、大部分の電流は R を流れる I1 となる。そのためAB間の電圧は RI1 で決まる(オームの法則)。それにより定まった電圧Vで rV を流れる電流 I2 が決まる(オームの法則)ので下図の様な電流計の電流値の読みでAB間の電圧が測定できることになる。
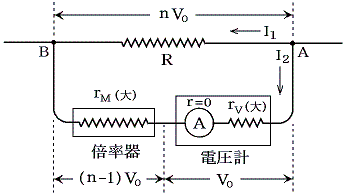
電圧計が測ることのできる最大電圧をV0とする。そのとき、そのn倍の電圧を測定するには電圧計に直列に抵抗rMの倍率器を設置し、そちらに(n−1)V0の電圧がかかるようにしてやればよい。直列回路では各部分にかかる電圧は、電流が共通だから、各部分の抵抗値に比例する。故に V0:(n−1)V0=rV:rM より rM=(n−1)rV とすればよい。
電圧の測定レンジが切り替えられる電圧計の内部は下図の様になっており、使用するときは測定電圧の大きさにより、接続端子(下図では−極)を切り替えておこなう。
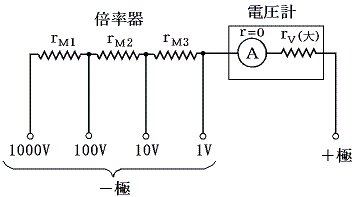
今電圧計の最大測定電圧が V0=1Vであるとする。そのとき各端子を利用した場合の測定最大電圧が標記の値になるためには倍率器の各抵抗値がいくらにならねばならないか計算してみよう。
1000V端子を利用する場合、電圧計rVにかかる電圧が最大値1Vになるようにするには、残りの999Vを抵抗(rM1+rM2+rM3)で支えねばならない。そのとき直列回路の電圧値は各部分の抵抗値に比例するので 1V:999V=rV:(rM1+rM2+rM3) が成り立つ。
同様に100V端子を利用する場合、rVにかかる電圧が1Vの場合、残り99Vが(rM2+rM3) にかかるようにしなければならない。それにゆえに 1V:99V= rV : (rM2+rM3) が成り立つ。
同様に10V端子を利用する場合、rVにかかる電圧が1Vの場合、残り9Vが rM3 にかかるようにしなければならない。それにゆえに 1V:9V= rV : rM3 が成り立つ。
上記4つの条件式を整理すると以下の連立方程式になる。
999rV=rM1+rM2+rM3 ・・・・・・(1)
99rV=rM2+rM3 ・・・・・・(2)
9rV=rM3 ・・・・・・(3)
未知数4個(rV、rM1、rM2、rM3)に対して式は3個だから未知数間の比が求まる。連立方程式の解として
rM1:rM2:rM3:rV=900:90:9:1
が得られる。つまり、全体としての抵抗値ができるだけ大きくなるよう心がけて、その間の比がこの値になるようにする。