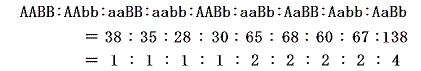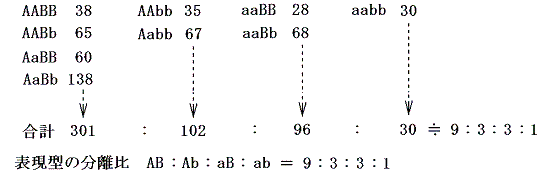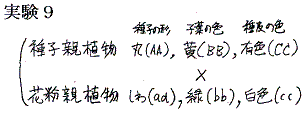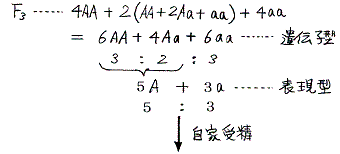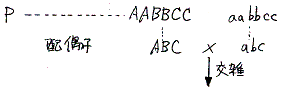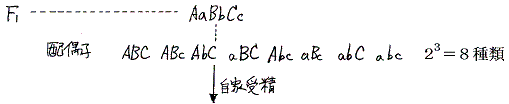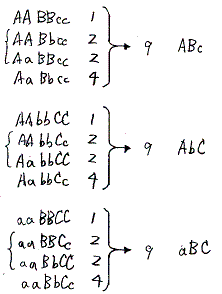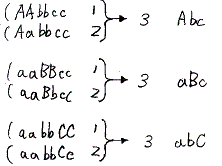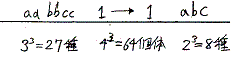このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
メンデルの遺伝法則と代数公式
1.導入
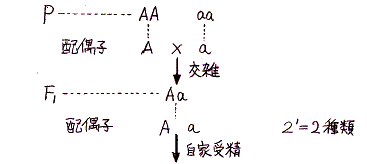
メンデルの実験は高校生物で習うので初等的な説明は省略し、教科書には載っていない所を説明する。以下の議論では対立形質は全て独立とし優劣の関係がハッキリしているとする。また両親にホモ接合体を用いて雑種第1代をつくり、それ以後の子孫はすべて自家受精を繰り返して作くられていくものとする。
普通遺伝学で言う雑種代1代(F1)とは、ある対立遺伝子をホモ接合でもつ両親(P)の間の交雑で生じた1代目の子を意味しており、たんなる1代目の子という意味とは違う。同様に雑種第2代(F2)とは前記F1の自家受精によってできた子を意味し、単なる2代目の子という意味ではない。以下同様で雑種第n代と言うところの子孫はその一つ前の雑種第(n−1)代の自家受精で作られたものを言う。
メンデル以前にも多くの交雑実験が行われ、遺伝法則を見つける試みはなされたのだがいずれも旨く行かなかった。メンデルがなぜ成功したのか、それは以下に述べる事情による。
- 両親にホモ接合の純系を用いた。(彼は純系を得るための予備実験に2年間を費やし、両親が純系であることを確信していた。)純系の親を得るにはエンドウ豆は最適な植物だった。
- 雑種第1代以後は全て自家受精のみでその子孫を得て、その表現型の分離比を追跡していった。実際メンデルは形質によっては最大で雑種第7代まで栽培している。自家受精で子供を作るのにエンドウ豆は最適な植物だった。
- エンドウ豆は自然状態で自家受精をし、自家受精を繰り返しても稔性可能(子孫が残せる)な種子をつけた。そのため上記1.2.の意味の実験に非常に適していた。また、統計的処理(つまり数を数えて分類・保存する)するのに最適な大きさの種子をつけた。つまりエンドウを実験材料に選んだことこそ成功の鍵だった。
- メンデルは厖大な数のエンドウを栽培して、厖大な数の種子を得て統計的な処理を実施した。特に雑種第2代、第3代の統計処理で明確な結論が得られるのに十分な数を栽培したことが成功の鍵だった。
2.メンデルの実験
メンデルの論文「植物雑種に関する実験」1866年発刊の日本語訳は何種類か出版されている。以下、その翻訳本である山本孝介訳「メンデリズムの基礎」裳華房に基づいて説明する。ただしメンデルは雑種の子孫について、F2を初代、F3を第2代と言っており、現代のF1を雑種第1代、F2を雑種第2代、・・・・・という呼び方と1代ずつずれている。ここでは、今日の呼び方に言い換えて説明する。
以下の表はメンデルが一つの形質に着目して行った7つの実験の結果である。ここで次の事柄に注意せよ。
- メンデルは両親の個体数は記載しているが、花粉親と卵親の個数や、どちらの親からどちらの親へ花粉を交配したかなどは記していない。どの実験でも相互交配(ある交配で卵親としたら他の交配では花粉親として用いる)したと記しているだけである。彼は交配に於いて花粉と卵細胞は同等であることをすでに知っていたし、また実験でそのことを確かめている。(メンデルの論文第4章、前掲訳本P32)
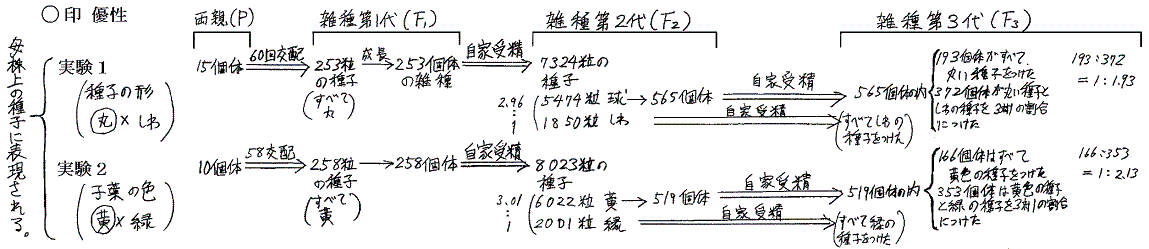
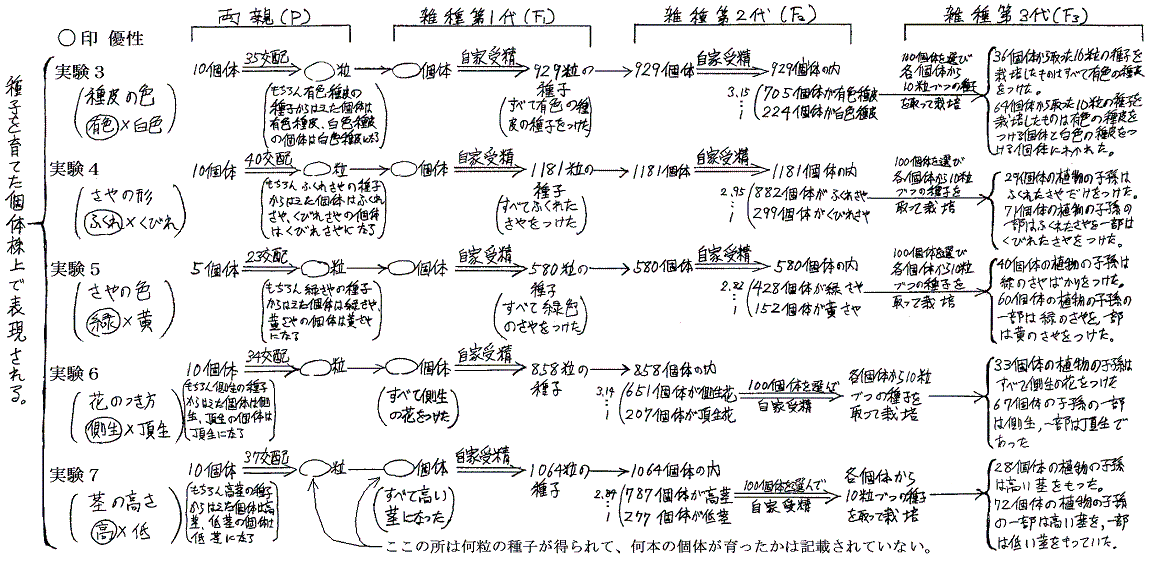
- 実験1、2と実験3〜7は本質的に異なる意味を持つ。実験1、2の形質は子供の形質で母株上の種子に現れるが、実験3〜7の形質は母体の形質なので種子を育てた個体株上で表現される。種子植物の有性生殖で習うように種皮、鞘(子房壁)、花弁、萼(がく)は親の体である。種皮の中に包まれている胚珠の部分のみが真の子供である。そのため雑種第n第と言うとき、栽培年度がずれていることに注意。図では縦列が揃う様に記してあるので比較して欲しい。(メンデルの論文第4章、前掲訳本P33)
- 雑種第2代(F2)までは全ての子供の種を蒔いて栽培しているが、雑種第3代以降は無作為に抽出した種子の栽培で追跡している。実験1、2については雑種第7代(F7)、実験3、7については雑種第6代(F6)、実験4、5、6については雑種第5代(F5)まで栽培して同様の結論を得たと記している。(メンデルの論文第7章、前掲訳本P43)
実験1〜7 (印刷はこちらのバージョン)
実験8 (印刷はこちらのバージョン) メンデルはさらに、2種類の対立形質が同時に遺伝する場合を実験している。
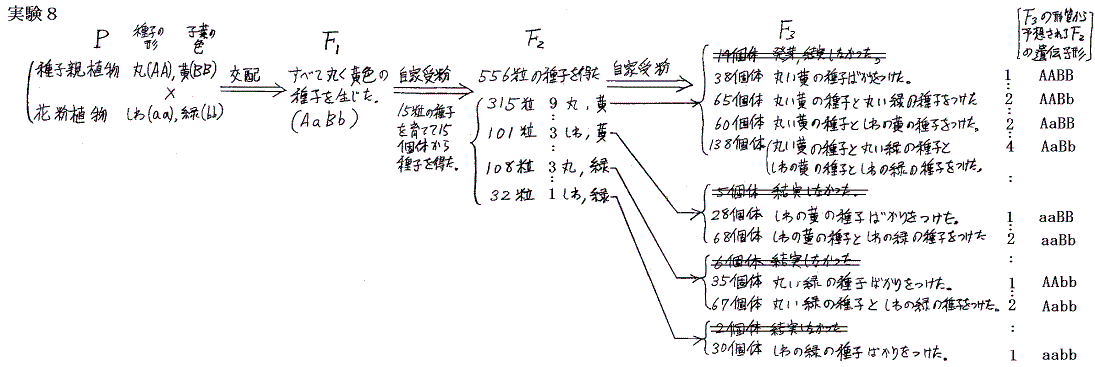
の結果を得ている。これから雑種第2代(F2)の遺伝子型分離比が
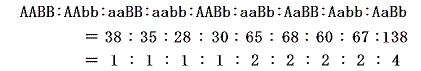
となることを明らかにした。しかしこれは非常に解りにくい分け方である。今日の教科書風に並べて表現型で数えると以下の様になる。
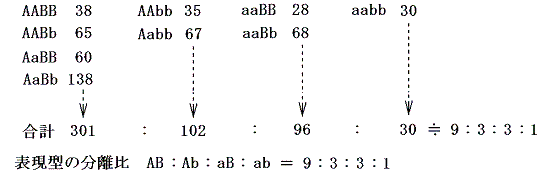
実験9 (印刷はこちらのバージョン) さらに3種類の形質について
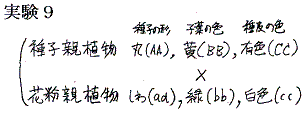
の交配実験を行った。そして交配で得た種子を育てて24株の雑種(F1)の個体を得た。そらの個体から687粒の種子(F2)を得て、次の年にそれらの種子を栽培すると639株の個体が育って果実をつけた。それら株のもとになった639粒の種子の遺伝子型は下記の割合あることが“その後の研究”で明らかになったと言っている。
メンデルは“その後の研究”の詳細を述べていないが、前記注意2で説明したように種皮の色は親の体の形質であり、種子の形、子葉の色は子の形質であるから発現する年度が1年ずれる。そのため雑種代3代(F3)、雑種代4代(F4)の表現型を数えて、かなり込み入った考察をする必要がある。いずれにしても、その遺伝子型の分離比は
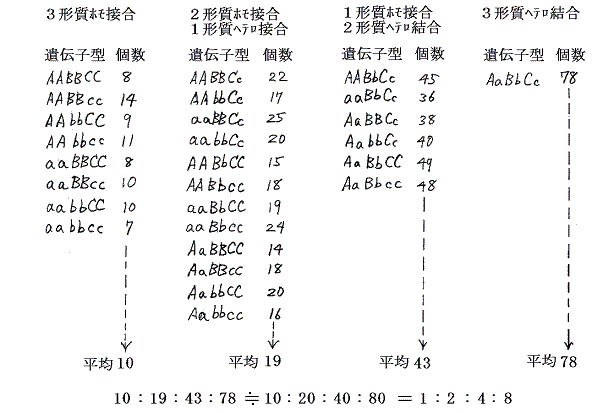
のようになったと報告している。しかし、これは非常に解りにくい分け方である。今日の教科書風に並べ直して表現型の分離比で表すと以下のようになる。

今日、子葉の色を発現する遺伝子と、種皮の色を発現する遺伝子は連鎖(同一の染色体上にある)していることが解っている。ただし、その染色体上の位置はかなり離れており、組み替えが頻繁におこる。そのため幸運にも、メンデルはそれらの遺伝子をほぼ独立と見なせる実験結果を得ることができた。
3.メンデルの遺伝法則
メンデルは2.で得られた実験結果を説明するために優性の法則、分離の法則、独立の法則を仮定した。そしてそれらを用いて実験結果を見事に説明し法則の正当性を明らかにした。これらは高校生物で習うところなので説明は省略して結論だけを簡単に復習する。メンデルの発見の歴史的な位置づけはこちらの年表を参照されたし。
(1)一遺伝子雑種(実験1〜7)
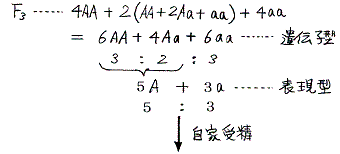

自家受精を繰り返していくと、世代を重ねるごとに純系ホモ接合のAAやaaの割合が増大し、ヘテロ接合Aaの割合が減少していく。これはメンデルの先駆者ゲルトナーやケルロイターがすでに気付いていたことであり、メンデルも明確に認識していた。そして雑種第n代ではAA:Aa:aaの分離比は (2n-1−1):2:(2n-1−1) になることを示している。(メンデルの論文第7章 前掲訳本P43〜44)
エンドウ豆は代々自家受精を繰り返して子孫を作る植物である。そのためメンデルは種子商で買ってきたエンドウ豆がほぼ純系のホモ接合体である確信があった。しかしメンデルは2年間予備的に栽培して自家受精した株で形質が混じって種をつけるものの子孫は全て取り除いた。そのため親植物として完全な純系ホモを用いることができた。(メンデルの論文第2章、前掲訳本P23〜24)
(2)二遺伝子雑種(実験8)
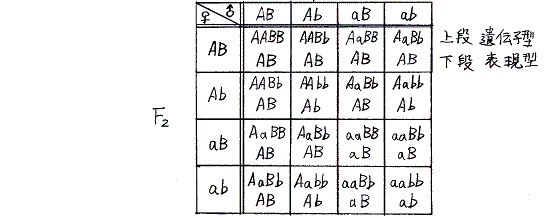

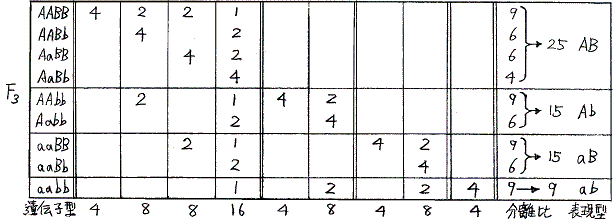
メンデルは上記F3の分離比からもとのF2の遺伝子型を推察した。二遺伝子雑種に於いても自家受精を繰り返すとAABBやaabbの純系ホモ接合体の割合が増大し、ヘテロ接合体の割合が減少するのが見て取れる。
(3)三遺伝子雑種(実験9)
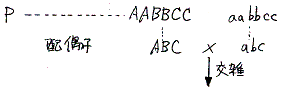
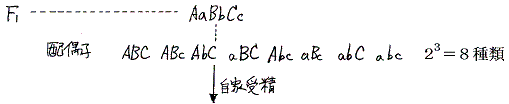
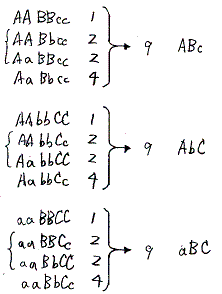
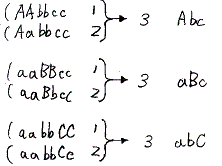
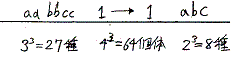
4.遺伝法則と代数計算
メンデルの法則を説明するために、普通は縦横に配偶子の遺伝子型を配置したマトリックス図を用います。これは非常に解りやすく便利ですが、対立遺伝子の数や雑種第n代というときのnが増えると、遺伝子型や表現型を数えるのが非常に面倒になります。そこでマトリックス図を代数計算で置き換える方法を説明する。最初に注意したことだが、以下の議論は全て両親にホモ接合体を用いて雑種第1代をつくり、それ以後の子孫のはすべて自家受精を繰り返して作くられていくものとする。
(1)一遺伝子雑種(実験1〜7)
- 両親を
- P・・・・・・・・・・AA×aa
- とすると
- F1・・・・・・・・・・・・Aa (表現型はA)
- となる。これにできる配偶子の種類は(A+a)だからF2は以下の代数的掛け算で計算できる。
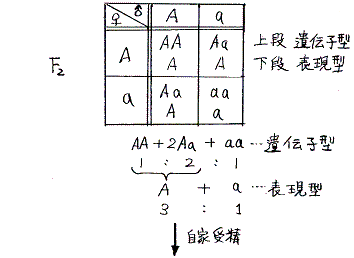
- F2・・・・(A+a)(A+a)=AA+2Aa+aa
ゆえに
AA、Aa、aaの遺伝子型分離比=1:2:1=(22-1−1):2:(22-1−1)
となる。AA、Aaの表現型をA、aaの表現型をaであらわすと
A、aの表現型分離比=(1+2):1=3:1
- となる。次にF2の自家受精でF3を作るとき、AA、Aa、aaの自家受精でできる種子の数を数える。Aaの自家受精はF2を作る手順と同じであるが、それぞれの一株に実る種子の総数を同じにするためAAやaaの自家受精もそれぞれ(A+A)(A+A)や(a+a)(a+a)の掛け算で種子ができるとする。そのときAA、Aa、aaの種子の割合はもともと1:2:1だからそのことも考慮して
- F3・・・1(A+A)(A+A)+2(A+a)(A+a)+1(a+a)(a+a)
=4AA+2(AA+2Aa+aa)+4aa
=6AA+4Aa+6aa
=定数×(3AA+2Aa+3aa)
ゆえに
AA、Aa、aaの遺伝子型分離比=3:2:3=(23-1−1):2:(23-1−1)
となる。さらに
A、aの表現型分離比=(3+2):3=5:3
- 同様な手順でF4の分離比を計算すると
- F4・・・・3(A+A)(A+A)+2(A+a)(A+a)+3(a+a)(a+a)
=3×4AA+2(AA+2Aa+aa)+3×4aa
=14AA+4Aa+14aa
=定数×(7AA+2Aa+7aa)
ゆえに
AA、Aa、aaの遺伝子型分離比=7:2:7=(24-1−1):2:(24-1−1)
となる。さらに
A、aの表現型分離比=(7+2):7=9:7
- 以下同様であるが、数学的帰納法を用いて雑種第n代の分離比を求めてみよう。まず雑種第(n−1)代の分離比が
- Fn-1のAA、Aa、aa遺伝子型分離比=(2(n-1)-1−1):2:(2(n-1)-1−1)=(2n-2−1):2:(2n-2−1)
- であるとすると、それの自家受精でできる雑種代n代の種子は
- Fn・・・・(2n-2−1)(A+A)(A+A)+2(A+a)(A+a)+(2n-2−1)(a+a)(a+a)
=(2n-2−1)×4AA+2(AA+2Aa+aa)+(2n-2−1)×4aa
=2×{(2n-2−1)×2+1}AA+2×2Aa+2×{(2n-2−1)×2+1}aa
=2×(2n-1−1)AA+2×2Aa+2×(2n-1−1)aa
=定数×{(2n-1−1)AA+2Aa+(2n-1−1)aa}
となる。ゆえに
AA、Aa、aaの遺伝子型分離比=(2n-1−1):2:(2n-1−1)
となる。さらに
A、aの表現型分離比={(2n-1−1)+2}:(2n-1−1)=(2n-1+1):(2n-1−1)
になる。
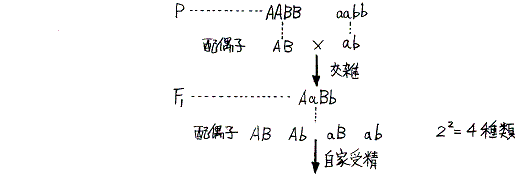
(2)二遺伝子雑種(実験8)
- 両親を
- P・・・・・・・・AABB×aabb
- とすると
- F1・・・・・・・・・・・・AaBb (表現型はAB)
- となる。これにできる配偶子の種類は(A+a)(B+b)となる。これは展開式AB+Ab+aB+abから明らか。だから前項2.(2)でF2の遺伝型分離比を求めるために用いたマトリックス図は次の代数計算で代用できる。
- F2・・・・{(A+a)(B+b)}{(A+a)(B+b)}
=(A+a)(B+b)(A+a)(B+b)
ここで以下のように順番を入れ替える。
=(A+a)(A+a)(B+b)(B+b)
=(AA+2Aa+aa)(BB+2Bb+bb)・・・・・・・・(1)
=AABB+2AABb+2AaBB+4AaBb+AAbb+2Aabb+aaBB+2aaBb+aabb・・・・・(2)
となる。ゆえに
AABB、AABb、AaBB、AaBb、AAbb、Aabb、aaBB、aaBb、aabbの遺伝子型分離比
=1:2:2:4:1:2:1:2:1
となる。ここでAABB・AABb・AaBB・AaBbの表現型をABで、AAbb・Aabbの表現型をAbで、aaBB・aaBbの表現型をaBで、aabbの表現型をabであらわすと
AB、Ab、aB、abの表現型分離比=(1+2+2+4):(1+2):(1+2):1=9:3:3:1
となりマトリックス法と同じ結論が得られる。
- 次にF2の自家受精でF3を作るとき、AABB、AABb、AaBB、AaBb、AAbb、Aabb、aaBB、aaBb、aabbの自家受精でできる種子の数を数える。AaBbの自家受精はF1からF2を作る手順と同じであるが、それぞれの一株に実る種の総数を同じにするためAABB、aabb等々の自家受精もそれぞれ{(A+A)(B+B)}{(A+A)(B+B)}、{(a+a)(b+b)}{(a+a)(b+b)}、等々の掛け算でおこなう。そのときF3にAABB、AABb、AaBB、AaBb、AAbb、Aabb、aaBB、aaBb、aabbの種子ができる割合は、もともとF2の種子の割合が1:2:2:4:1:2:1:2:1であることを考慮して
- F3・・・・{1(A+A)(B+B)}{(A+A)(B+B)}+2{(A+A)(B+b)}{(A+A)(B+b)}+2{(A+a)(B+B)}{(A+a)(B+B)}+4{(A+a)(B+b)}{(A+a)(B+b)}+1{(A+A)(b+b)}{(A+A)(b+b)}+2{(A+a)(b+b)}{(A+a)(b+b)}+1{(a+a)(B+B)}{(a+a)(B+B)}+2{(a+a)(B+b)}{(a+a)(B+b)}+1{(a+a)(b+b)}{(a+a)(b+b)}・・・・・・・・(3)
- となる。しかしこのやり方は見通しが悪い。(3)式は前記(2)式の各項をそれぞれの自家受精に相当する項目で置き換えたものであるが、この式は前記(1)式のAAを(A+A)(A+A)、Aaを(A+a)(A+a)、aaを(a+a)(a+a)、BBを(B+B)(B+B)、Bbを(B+b)(B+b)、bbを(b+b)(b+b)で置き換えた後に代数展開したものと同じである。だから(2)式を出発点にするよりも(1)式を出発点にする方が一遺伝子雑種の結論を利用するのに都合がよい。。そうすると
- F3・・・・{1(A+A)(A+A)+2(A+a)(A+a)+1(a+a)(a+a)}{1(B+B)(B+B)+2(B+b)(B+b)+1(b+b)(b+b)}
となる。ここで{ }括弧の中は一遺伝子雑種で計算した事柄で
={4AA+2(AA+2Aa+aa)+4aa}{4BB+2(BB+2Bb+bb)+4bb}
={6AA+4Aa+6aa}{6BB+4Bb+6bb}
=定数×(3AA+2Aa+3aa)(3BB+2Bb+3bb)・・・・・・・・(4)
となる。ゆえに
AABB、AABb、AaBB、AaBb、AAbb、Aabb、aaBB、aaBb、aabbの遺伝子型分離比
=(4)式を代数展開した各項の係数比になる。
となる。さらに
AB、Ab、aB、abの表現型分離比
=(3A+2A+3a)(3B+2B+3b)
=(5A+3a)(5B+3b)を代数展開した各項の係数比
になる。
- 同様に(3)式を展開した式ではなく、もとの(4)式を出発点としてF4の分離比を計算すると
- F4・・・・{3(A+A)(A+A)+2(A+a)(A+a)+3(a+a)(a+a)}{3(B+B)(B+B)+2(B+b)(B+b)+3(b+b)(b+b)}
={3×4AA+2(AA+2Aa+aa)+3×4aa}{3×4BB+2(BB+2Bb+bb)+3×4bb}
={14AA+4Aa+146aa}{14BB+4Bb+14bb}
=定数×(7AA+2Aa+7aa)(7BB+2Bb+7bb)・・・・・・・・(5)
となる。ゆえに
AABB、AABb、AaBB、AaBb、AAbb、Aabb、aaBB、aaBb、aabbの遺伝子型分離比
=(5)式を代数展開した各項の係数比になる。
となる。さらに
AB、Ab、aB、abの表現型分離比
=(7A+2A+7a)(7B+2B+7b)
=(9A+7a)(9B+7b)を代数展開した各項の係数比になる。
- 同様な考え方で雑種第n代の分離比は、一遺伝子雑種の場合に数学的帰納法を用いて求めた雑種代n代の分離比の結論が使えて
- Fn・・・・定数×{(2n-1−1)AA+2Aa+(2n-1−1)aa}{(2n-1−1)BB+2Bb+(2n-1−1)bb}・・・・・(6)
となる。ゆえに
AABB、AABb、AaBB、AaBb、AAbb、Aabb、aaBB、aaBb、aabbの遺伝子型分離比
=(6)式を代数展開した各項の係数比
となる。さらに
AB、Ab、aB、abの表現型分離比
={(2n-1−1)A+2A+(2n-1−1)a}{(2n-1−1)B+2B+(2n-1−1)b}
={(2n-1+1)A+(2n-1−1)a}{(2n-1+1)B+(2n-1−1)b}を代数展開した各項の係数比
になる。
(3)三遺伝子雑種(実験9)
- 両親を
- P・・・・・・・・AABBCC×aabbcc
- とすると
- F1・・・・・・・・・・・・・AaBbCc (表現型はABC)
- となる。これにできる配偶子の種類は(A+a)(B+b)(C+c)となる。これは展開式ABC+ABc+AbC+aBC+Abc+aBc+abC+abcから明らか。だから前項2.(3)でF2の遺伝型分離比を求めるために用いたマトリックス図は次の代数計算で代用できる。
- F2・・・・{(A+a)(B+b)(C+c)}{(A+a)(B+b)(C+c)}
=(A+a)(B+b)(C+c)(A+a)(B+b)(C+c)
ここで以下のように順番を入れ替える。
=(A+a)(A+a)(B+b)(B+b)(C+c)(C+c)
=(AA+2Aa+aa)(BB+2Bb+bb)(CC+2Cc+cc)・・・・・・・・(7)
となる。ゆえに
F2の遺伝子型の分離比=(7)式を代数展開した各項の係数比
となる。さらに(7)式においてAAとAa→A、aa→a、BBとBb→B、bb→b、CCとCc→C、cc→cに変換すると
(A+2A+a)(B+2B+b)(C+2C+c)=(3A+a)(3B+b)(3C+c)・・・・(8)
が得られる。ゆえに
F2の表現型の分離比=(8)式を代数展開した各項の係数比
となりマトリックス法と同じ結論が得られる。
- 次にF2の自家受精で作ったF3の種子の遺伝子型分離比を求めるには二遺伝子雑種の場合と同様に(7)式を基礎にすればよい。そのとき分離比を求めるための代数式は一遺伝子雑種の結論が使えて
- F3・・・(3AA+2Aa+3aa)(3BB+2Bb+3bb)(3CC+2Cc+3cc)・・・・・・・・(9)
となる。ゆえに
F3の遺伝子型分離比=(9)式を代数展開した各項の係数比
となる。さらにF2と同様に考えて
(3A+2A+3a)(3B+2B+3b)(3C+2C+3c)=(5A+3a)(5B+3b)(5C+3c)・・・・(10)
が得られるので
F3の表現型分離比=(10)を代数展開した各項の係数比
となる。
- 以下同様で
- F4の遺伝子型分離比=(7AA+2Aa+7aa)(7BB+2Bb+7bb)(7CC+2Cc+7cc)を代数展開した係数比
となる。さらに
F4の表現型分離比=(9A+7a)(9B+7b)(9C+7c)を代数展開した係数比
となる。
- 雑種第n代の分離比については
- 遺伝子型分離比={(2n-1−1)AA+2Aa+(2n-1−1)aa}{(2n-1−1)BB+2Bb+(2n-1−1)bb}{(2n-1−1)CC+2Cc+(2n-1−1)cc}
表現型分離比={(2n-1+1)A+(2n-1−1)a}{(2n-1+1)B+(2n-1−1)b}{(2n-1+1)C+(2n-1−1)c}
- となる。
(4)m遺伝子雑種の雑種第n代の分離比
独立の対立遺伝子がm対ある雑種第n代の分離比も前記の方法でもとまる。そのとき以下のことに注意すれば十分である。

m個の対立形質は全て独立。ヘテロ接合体には全て優劣の関係がある。純系ホモ接合体の両親の交雑で生じ、以下の子孫は全て自家受精でふえる場合。
遺伝子型分離比は
{(2n-1−1)AA+2Aa+(2n-1−1)aa}{(2n-1−1)BB+2Bb+(2n-1−1)bb}・・・{(2n-1−1)MM+2Mm+(2n-1−1)mm}
の代数展開でもとまる。
表現型分離比は
{(2n-1+1)A+(2n-1−1)a}{(2n-1+1)B+(2n-1−1)b}・・・{(2n-1+1)M+(2n-1−1)m}
の代数展開でもとまる。
(5)計算例
例1 メンデルの実験1のF7 (m=1、n=7の場合)
- 遺伝子型 2n-1−1=27-1−1=26−1=63 3m=31=3項
- 63AA+2Aa+63aa=63:2:63
- 表現型 2n-1+1=27-1+1=26+1=65 2m=21=2項
- 65A+63a=65:63
例2 メンデルの実験8のF3 (m=2、n=3の場合)
- 遺伝子型 2n-1−1=23-1−1=22−1=3 3m=32=9項
- (3AA+2Aa+3aa)(3BB+2Bb+3bb)
=9AABB+6AABb+6AaBB+4AaBb+9AAbb+6Aabb+9aaBB+6aaBb+9aabb
=9:6:6:4:9:6:9:6:9
- 表現型 2n-1+1=23-1+1=22+1=5 2m=22=4項
- (5A+3a)(5B+3b)
=25AB+15Ab+15aB+9ab
=25:15:15:9
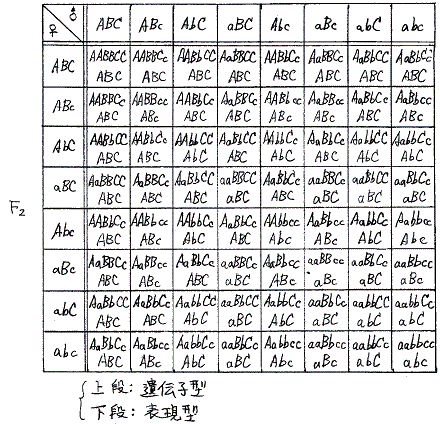
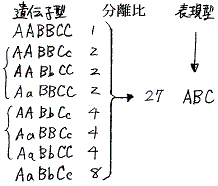
例3 メンデルの実験9のF2 (m=3、n=2の場合)
- 遺伝子型 2n-1−1=22-1−1=21−1=1 3m=33=27項
- (AA+2Aa+aa)(BB+2Bb+bb)(CC+2Cc+cc)
=AABBCC+2AABBCc+2AABbCC+2AaBBCC+4AABbCc+4AaBBCc+4AaBbCC+8AaBbCc
+AABBcc+2AABbcc+2AaBBcc+4AaBbcc
+AAbbCC+2AAbbCc+2AabbCC+4AabbCc
+aaBBCC+2aaBBCc+2aaBbCC+4aaBbCc
+AAbbcc+2Aabbcc
+aaBBcc+2aaBbcc
+aabbCC+2aabbCc
+aabbcc
=1:2:2:2:4:4:4:8:1:2:2:4:1:2:2:4:1:2:2:4:1:2:1:2:1:2:1
- 表現型 2n-1+1=22-1+1=21+1=3 2m=23=8項
- (3A+a)(3B+b)(3C+c)
=27ABC+9ABc+9AbC+9aBC+3Abc+3aBc+3abC+abc
=27:9:9:9:3:3:3:1
となりマトリックス図で求めたのと同様な結論が得られる。